Задача коммивояжёра
Постановка задачи
При обсуждении метода "грубой силы" (последовательный перебор) была сформулирована задача коммивояжёра:
Eсть N городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз.Расстояние из города j в город i считается неотрицательным числом: Dji ≥ 0. Это не обязательно "физическая длина" дороги. "Расстоянием" может быть время перемещения, стоимость билета или произвольное неотрицательное число. Часто Dji называют стоимостью ребра (edge costs), так как дороги можно представить рёбрами (edges), соединяющими города-вершины (vertices) некоторого графа.
Приведём небольшую классификацию вариантов задачи:
- Симметричная проблема коммивояжёра (TSP = traveling salesman problem) в которой расстояния заданы между любыми двумя городами и матрица расстояний симметрична: Dji = Dij.
- Асимметричная проблема коммивояжёра (ATSP) допускает несимметричность матрицы Dji ≠ Dij. В ещё более общем случае, пути между некоторыми городами могут отсутствать (== иметь бесконечную длину).
- Задача с частичным упорядочиванием (SOP = sequential ordering problem) требующая, чтобы определённый город i был посещён до города j (таких условий может быть несколько).
- Поиск цикла Гамильтона (HCP = нamiltonian cycle problem) - обнаружение в произвольном графе замкнутых путей, проходящих через каждую вершину в точности один раз.
В TSP (симметричной задаче коммивояжёра) путь замкнут и стартовать можно с любого города (и в любую сторону). Поэтому для N городов существует (N-1)!/2 различных путей. Факториал растёт очень быстро: N! ~ NN и пространство в котором ищется оптимальное решение оказывается огромным. Именно поэтому задача коммивояжёра интересна для тестирования различных алгоритмов.
Евклидова задача коммивояжёра
Если Dji = Dij и расстояния между любыми городами i, j, k удовлетворяют неравенству треугольника: Dij + Djk ≥ Dik, то задачу коммивояжёра называют метрической. Её частным случаем является задача соединения кратчайшей замкнутой ломаной линией точек на плоскости (расстояние равно обычному евклидовому расстоянию). Ниже приведены решения такой задачи для 20 и 50 городов:
Несложно видеть, что в евклидовой задача коммивояжёра (ETSP) оптимальный путь не должен иметь пересечений. Действительно, пусть есть некоторый путь, изображённый ниже на первом рисунке. Пунктиром обозначены остальные его участки (т.е. приведены только 4-е города). Если перебросить два участка пути (как на второй картинке), то общий путь вырастет (сумма диагоналей 4-угольника всегда длиннее суммы двух противоположных сторон):
С ETSP связаны интересные вопросы статистического характера. Рассмотрим, например, квадрат в котором случайно, с равномерным распределением размещено N городов. Оказывается, что в большинстве случаев такие "карты городов" имеют кратчайшие пути примерно одной длины, пропорциональной квадратному корню из N.
Методы решения
Задача коммивояжёра относится к классу NP-трудных и не известен алгоритм, который позволет гарантировано её решить за полиномиальное по числу городов N время T ~ Nk, k=const. Тем не менее, для "обозримого" количества городов существует множество способов решения:
1. Точные методы не только находят некоторое решение, но и при окончании своей работы доказывают, что это решение - наилучшее. Отметим следующие из них:
- Полный перебор перестановок N-1 чисел (стартовый город фиксирован). Практически бесполезен при N > 15.
- Направленный поиск с возвратами - перебор вариантов "вокруг" некоторого решения с отсечением путей, имеющих длину большую, чем лучший к текущему моменту путь.
- Метод ветвей и границ - наиболее эффективный из известных метод отсечения "неперспективных" узлов, за счёт анализа матрицы расстояний. При поиске оптимального решения строится бинарное дерево (в каждом узле порождаются 2 ветви: коммивояжёр идёт в некоторый город или не идёт в него).
- Линейное программирование применяется для минимизации (с ограничениями) линейной формы d·x, где x - искомый бинарный вектор размерности N(N-1)/2, компоненты которого xi равны 1 или 0, в зависимости от того, входит i-е ребро в путь или нет. Вектор d (той же размерности) равен длинам рёбер.
2. Эвристические методы, обычно, существенно быстрее точных, однако они не гарантируют оптимальности найденного решения. Результат их комбинации может далее использоваться как первое приближение для последующего улучшения, например, при помощи поиска с возвратом:
- Жадный алгоритм при выборе очередного города берёт ближайший не посещённый до этого город.
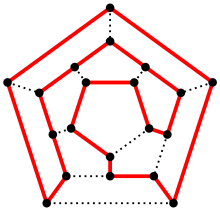
- Метод шнурка - геометрическая вариация жадного алгоритма, в которой города охватываются замкнутым контуром. Он постепенно растягивается, стараясь пройти через все города, минимальным образов увеличив свою длину.
- Скользящий перебор переставляет местами города из небольшой части пути. Затем такое "окно перебора" скользит вдоль всего пути. Метод имеет различные вариации и оказывается эффективным способом улучшения решения, найденного предыдущими двумя эвристическими методами.
3. Вероятностные методы фактически ни когда не останавливаются, совершая случайные изменения пути, в ожидании получения более короткого. Из этого класса методов отметим:
- Метод отжига в котором происходят перестановки городов с постепенно "затухающей" интенсивностью. При этом постоянно сохраняется наилучшее найденное решение.
- Генетический алгоритм - более "продвинутый" вариант, при котором создаётся большое количество различных путей. Они постоянно "мутируют" и "скрещиваются" друг с другом, обмениваясь отдельным участками.
Немного истории
По-видимому первая задача, связанная с проблемой коммивояжёра была поставлена и решена Леонардом Эйлером в 1757 г. Он предложил найти замкнутый путь для коня на шахматной доске. Соответствующее решение, найденное самим Эйлером, приведено ниже, слева:
|
|
Полезные ресурсы
- TSPLib - проект, развивающийся с 1990-х. Содержит карты с массивами координат реальных городов и оптимальный TSP-путь. Является отличным источником для тестирования алгоритмов. Современная поддержка проекта находится здесь.
- Книга - "The Traveling Salesman Problem: A Computational Study", D.L. Applegate, R.E. Bixby, V. Chvátal & W.J. Cook (2006).
- Concorde TSP solve - программа с открытым кодом, решающая задачу коммивояжёра методами линейного программирования. Один из её рекордов - нахождение пути в ETSP с 85900 городами.