Многомерное шкалирование
Введение
Многомерное шкалирование - это методы визуализации многомерных данных. Пусть имеется n-мерное пространство признаков, в котором каждый объект описывается координатами x={x1,...,xn} (номера признаков помечаем верхними индексами). В пространстве находится N объектов с координатами x1,...,xN (нижний индекс - номер объекта). Необходимо отобразить это пространство на m-мерное пространство в координатах y={y1,...,ym}, где m существенно меньше n (обычно m=2 или m=3). При этом исходная структура данных должна быть сохранена. В частности, объекты близкие в пространстве x, должны быть близки и в пространстве y.
Минимизация расстояний
В качестве меры близости объектов с координатами a и b будем использовать евклидово расстояние: d(a,b)=∥a−b∥=√(a−b)2=√(a1−b1)2+...+(an−bn)2 и аналогично в m-мерном пространстве. Напомним, что евклидово расстояние подразумевает, что все признаки объектов имеют равную дисперсию, независимы и одинаково важны при классификации (дают равный вклад в расстояние между объектами).
Обозначим расстояния между объектами в обоих пространствах следующим образом (они симметричны по индексам i,j):
Dij=∥xi−xj∥, dij=∥yi−yj∥.
Критерий совпадения величин Dij и dij задаётся той или иной функцией ошибок Cost.
Она зависит от положения объектов y1,...yN в m-мерном пространстве (в n-мерном пространстве они заданы).
Минимизация функции ошибок проводится градиентным методом. Вычислим производную Cost по yp.
От координат p-того объекта зависят расстояния dp1,...,dpN (в списке нет dpp), поэтому:
∂Cost∂yp=i≠p∑i∂Cost∂dpi∂dpi∂yp=i≠p∑i∂Cost∂dpiyp−yidpi.
 В градиентном методе минимизации функции Cost необходимо задать в m-мерном пространстве координаты объектов y1,...,yN случайным образом.
Затем на каждой итерации их подправлять:
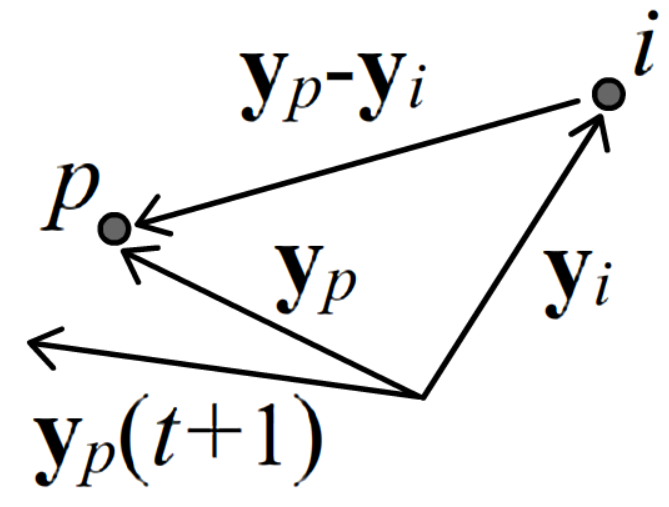
yp(t+1)=yp(t)−gi≠p∑i1dpi∂C∂dpi(yp(t)−yi(t)),
где g - скорость обучения.
Множитель при yp(t)−yi(t) обычно интерпретируется как некая "сила", действующая на p-тую частицу
со стороны i-той частицы. Если производная ∂C/∂dpi положительна - p-я частица притягивается к i-й,
а если отрицательна - отталкивается (см. рисунок справа для ∂C/∂dpi<0).
В градиентном методе минимизации функции Cost необходимо задать в m-мерном пространстве координаты объектов y1,...,yN случайным образом.
Затем на каждой итерации их подправлять:
yp(t+1)=yp(t)−gi≠p∑i1dpi∂C∂dpi(yp(t)−yi(t)),
где g - скорость обучения.
Множитель при yp(t)−yi(t) обычно интерпретируется как некая "сила", действующая на p-тую частицу
со стороны i-той частицы. Если производная ∂C/∂dpi положительна - p-я частица притягивается к i-й,
а если отрицательна - отталкивается (см. рисунок справа для ∂C/∂dpi<0).
Sammon mapping
Простейший выбор функции ошибок был предложен J.W. Sammon в 1969: Cost=k<q∑k,q(dkq−Dkq)2Dkq. Функция ошибок Cost является суммой квадратичных отклонений расстояний между объектами в обоих пространствах. Такая сумма должна быть минимальной. При этом вес больших расстояний (см. знаменатель) меньше, чем вес маленьких расстояний. Знак k<q над суммой подразумевает, что первый индекс суммирования всегда меньше второго: k<q∑k,qSkq≡12k≠q∑k,qSkq≡N∑k=1N∑q=k+1Sqk=S12+S13+...+S1N+S23+S24+...+S2N+...+SN−1,N. Несложно видеть (скажем для p=1), что ∂C∂dpi=2dpi−DpiDpi. Поэтому итерации градиентного метода выглядят следующим образом (множитель 2 включаем в g): yp(t+1)=yp(t)−gi≠p∑idpi−DpiDpidpi(yp(t)−yi(t)). Если dpi>Dpi объекты притягиваются (уменьшая тем самым расстояние dpi). В противном случае, они отталкиваются.
Стохастическое вложение соседей (SNE)
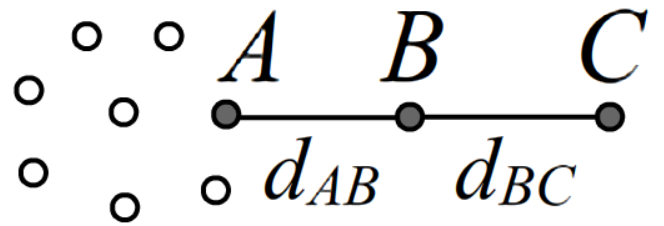 Минимизация разности расстояний в двух различных пространствах не учитывает скученности объектов.
Так, на рисунке справа можно предположить, что важнее сохранить
расстояние между объектами A и B, чем между B и C (объект C, удалённый от сгущения может быть
ошибкой или случайным выбросом). Поэтому стоит использовать меру близости, учитывающую
густоту или разреженность объектов в пространстве.
Минимизация разности расстояний в двух различных пространствах не учитывает скученности объектов.
Так, на рисунке справа можно предположить, что важнее сохранить
расстояние между объектами A и B, чем между B и C (объект C, удалённый от сгущения может быть
ошибкой или случайным выбросом). Поэтому стоит использовать меру близости, учитывающую
густоту или разреженность объектов в пространстве.
В 2002 Hinton и Roweis предложили метод "Стохастического вложения соседей" (Stochastic Neighbor Embedding, SNE), в котором учитывается плотность распределения объектов. Позднее, в 2008 Maaten и Hinton его несколько модифицировали, назвав "t-SNE методом".
Идея SNE-метода состоит в записи распределения вероятностей объектов в n-мерном и m-мерном пространствах. Координаты y={y1,...,ym} объектов в m-мерном пространстве подбираются таким образом, чтобы эти распределения были максимально похожи.
Пусть вероятность того, что в точке x окажется объект, соседний к объекту xk (и отличный от него) равна: Pk(x)=1Zke−αk(x−xk)2, Zk=i≠k∑ie−αk(xi−xk)2, Pk(xk)=0, где αk - некоторые константы, а нормировочный множитель Zk означает, что вероятности нормируются на единицу по всем объектам: i≠k∑iPk(xi)=1. Величина Pk(xi) интерпретируется как условная вероятность обнаружить объект в xi, если есть объект в xk. Чем дальше точка x от xk, тем менее вероятнее там встретить соседа k-того объекта. Отметим, что в общем случае Pi(xj)≠Pj(xi).
Выбор параметров вероятностей SNE
Параметры αk уникальны для каждого объекта. Они выбираются тем большими, чем выше плотность объектов вокруг xk. Для этого вычисляется энтропия распределения: Hk=−N∑i=1Pk(xi)lnPk(xi) и параметры αk подбираются так, чтобы Hk была постоянна для всех k.
Чтобы пояснить такой выбор αk, поставим численный эксперимент. Сгенерим в n-мерном пространстве облако объектов (N=1001) с нулевым средним положением и нормально распределённым расстоянием от центра координат с волатильностями σ=1,2,3,4,5. Чем σ больше, тем менее плотное распределение частиц возле начала координат. Зададим α=1/(2σ2) и вычислим энтропию относительно точки x=0 при разных размерностях пространства:
σ α H(n=10) H(n=100) 1 0.500 6.808 6.808 2 0.125 6.822 6.808 3 0.056 6.812 6.810 4 0.031 6.809 6.818 5 0.020 6.804 6.802
Как видно, она постоянна, поэтому выбор параметра α при фиксированной энтропии Hk=const, действительно, отражает плотность распределения частиц.
Отметим, что при энтропию быстрее вычислять при помощи эквивалентной формулы: Hk=lnZk+αkZkN∑i=1e−αk(x−xk)2 (xi−xk)2
Функция ошибки SNE
В качестве распределения вероятностей в m-мерном пространстве выбирается Qk(x)=1Zke−(y−yk)2, Zk=i≠k∑ie−(yi−yk)2, Qk(yk)=0. В отличии от n-мерного пространства вероятности имеют одинаковый множитель при расстояниях в показателях экспонент. Это подразумевает, что в пространстве m=2 или m=3 объекты окажутся распределёнными с примерно равной плотностью (да и подбирать дополнительные параметры проблематично).
Выберем функцию ошибки (=функцию стоимости), следуя теории информации, в виде расстояния Кульбака-Лейблера между двумя распределениями вероятностей: Cost=i≠j∑i,jPi(xj)lnPi(xj)Qi(yj), j≠i∑iQi(yj)=1. В силу нормировочного условия на Qi(yj), эта величина достигает минимального значения (нуля) когда все Qi(yj)=Pi(xj).
Градиент SNE
Вычислим производную функции ошибок Cost по расстояниям dpq. При взятии производной от симметричного тензора необходимо учитывать формулу: ∂dij∂dpq=δipδjq+δiqδjp, где δip - символ Кронекера, равный 1 при i=p и 0 при i≠p. Действительно, в соотвествии с этой формулой например, ∂d12/∂d12=∂d12/∂d21=1, а, скажем, ∂d12/∂d13=0. В связи с этим, имеем: ∂Cost∂dpq=−i≠j∑i,jPi(xj)Qi(yj)∂Qi(yj)∂dpq=i≠j∑i,jPi(xj)[2dij(δipδjq+δiqδjp)+1Zi∂Zi∂dpq] = 2dpq[Pp(xq)+Pq(xp)]+∑i1Zi∂Zi∂dpq, где в последнем слагаемом сумма по j положена единице в силу нормировочного условия на Pi(xj). Производная нормировочного множителя равна (учитываем, что diqδip≡dpqδip): ∂Zi∂dpq=j≠i∑j∂e−d2ij∂ dpq=−2j≠i∑je−d2ij dij(δipδjq+δiqδjp)=−2Zidpq (Qi(yq) δip+Qi(yp) δiq). В результате "сила", действующая на p-й объект со стороны q-тых объектов, равна: 1dpq∂Cost∂dpq=2(Pp(xq)−Qp(yq)+Pq(xp)−Pq(yp)). Соответственно, итерации по уточнению положения объектов в m-мерном пространстве имеют вид: yp(t+1)=yp(t)−gq≠p∑q(Pp(xq)−Qp(yq)+Pq(xp)−Pq(yp))(yp(t)−yq(t)).
Метод t-SNE
В методе t-SNE, по сравнению с SNE, сделаны два изменения. Во-первых, от несимметричных "условных" вероятностей в n-мерном пространстве переходят к симметричным "совместным" вероятностям: Pij=P(xi,xj)=Pi(xj)+Pj(xi)2N Число объектов N в знаменателе подразумевает следующую нормировку вероятностей: i≠j∑i,jPij=1.
Для вероятностей в m-мерном пространстве берётся распределение Коши или эквивалентно t-распределение Стьюдента с одной степенью свободы (отсюда приставка "t-" в названии метода): Qij=Q(yi,yj)=1/Z1+(yi−yj)2, Z=i≠j∑i,j11+(yi−yj)2, i≠j∑i,jQij=1. Вероятности Qij, как и Pij, симметричны: Qij=Qji.
Для функции ошибок по-прежнему выбирается расстояние Кульбака-Лейблера: Cost=i≠j∑i,jPijlnPijQij.
Градиент t-SNE
Вычисление градиента в t-SNE методе производится аналогично: ∂Cost∂dpq=−i≠j∑i,jPijQij∂Qij∂dpq=i≠j∑i,jPij[2dij(δipδjq+δiqδjp)1+d2ij+1Z∂Z∂dpq]=4dpqPpq1+d2pq+1Z∂Z∂dpq, где в последнем слагаемом учтено нормировочное условие на Pij. Ещё одно дифференцирование: ∂Z∂dpq=j≠i∑i,j∂(1+d2ij)−1∂ dpq=−2j≠i∑i,jdij(δipδjq+δiqδjp)(1+d2ij)2=−4dpq(1+d2pq)2 приводит к финальному, достаточно простому выражению для "силы": 1dpq∂Cost∂dpq=4Ppq−Qpq1+(yp−yq)2. Итерации по уточнению положения объектов в m-мерном пространстве t-SNE метода имеют вид: yp(t+1)=yp(t)−gq≠p∑qPpq−Qpq1+(yp−yq)2 (yp(t)−yq(t))+m⋅(yp(t)−yp(t−1)), где последнее слагаемое является инерционным (метод тяжёлого шарика, 0≤m≤1).
Параметры обучения
Авторы (Maaten и Hinton) рекомендуют в 2-мерном пространстве задавать случайное положение объектов с нормальным распределением с нулевым средним и маленькой 10−4 дисперсией (волатильность 10−2).
Мои эксперименты показывают, что в итерационную формулу стоит добавить ещё один параметр α, а авторы включают также параметр β: yp(t+1)=yp(t)−gq≠p∑qβPpq−Qpq1+α(yp−yq)2 (yp(t)−yq(t))+m⋅(yp(t)−yp(t−1)), На начальных стадиях обучения α выбирается малым (α=0.1−0.2), чтобы объектам легче было "проталкиваться" к своим соседям через облако остальных объектов. Постепенно, этот параметр повышается до единицы. Параметр скорости обучения в методе t-SNE у меня достаточно высок (g=1000−5000), хотя авторы рекомендуют значение 100 с адаптивным увеличением по алгоритму Jacobs (1988). Параметр инерции, обычно, равен m=0.5. Авторы рекомендуют его повысить до 0.8 после 250 итераций.
Авторы также дают ряд эзотерических советов. Например, умножать Pij на β=4 в начальных стадиях (50 итераций) оптимизации (early exaggeration), затем возвращать его к теоретическому значению β=1. Ещё один трюк, названный ранней компрессией (early compression) добавляет L2-штрафы в функцию ошибок, которые пропорциональны сумме квадратов расстояний объектов от начала координат. В формуле итерций это даёт дополнительный член γyp(t). При этом предполагается, что когда расстояния между объектами невелики, кластерам легче проходить друг через друга (выше у меня для этого служит параметр α)
Энтропия (в терминах натурального логарифма) обычно выбирается равной порядка 3.7 Чем меньше энтропия, тем более "ажурные" получаются кластеры.
Самостоятельно поиграться с параметрами обучения можно здесь.