Задача: Polygonal Areas
Постановка задачи
Необходимо нарисовать замкнутый полигон,
соединяющий N точек, находящихся в узлах решетки размером N × N.
При этом должны выполнятся следующие ограничения:
- На любой строчке или колонке сетки находится одна и только одна точка.
- Стороны полигона не пересекаются (кроме соединения в общей точке).
- У полигона нет параллельных сторон.
Ниже приведены 4 полигона для сетки 6 x 6. Первые три не удовлетворяют условиям задачи:
|
|
|
|
|
| Ошибка: Две вершины в одной строке |
Ошибка: Две стороны пересекаются |
Ошибка: Две стороны имеют одинаковый наклон |
Полигон удовлетворяет всем условиям |
Задача была сформулирована в рамках Al Zimmermann's Programming Contests в 2016-2017 г. Предлагалось найти положение точек и проведенный через них полигон с минимальной и максимальной площадью для 25 различных N:
5, 7, 11, 17, 23, 29, 37, 47, 59, 71, 83, 97, 113, 131, 149, 167, 191, 223, 257, 293, 331, 373, 419, 467, 521
В этом соревновании участвовало более 300 человек из различных стран.
Естественно, вычислительные мощности у них существенно отличались.
Однако, как мы увидим ниже, пространство поиска в этой задаче очень велико.
Поэтому метод "грубой силы" и его аналоги не работают в принципе и
выбор оптимальной стратегии поиска выходит на первое место.
Для каждого N в решениях всех участников выбирался самый большой и самый маленький полигон. Разница их площадей называлась "Best Raw Score". У каждого участника, в каждой задаче было своё "Raw Score", равное разнице максимальной и минимальной площади, которые ему удалось найти. Число очков за данную задачу равнялось отношению "Raw Score" участника к лучшей разнице "Best Raw Score". Соответственно, за 25 задач можно было набрать максимум 25 очков (если все найденные решения оказывались лучшими). Алгоритм, описываемый ниже, в браузере на обычном компьютере привёл к следующим баллам по каждой задаче (в сумме 24.6):
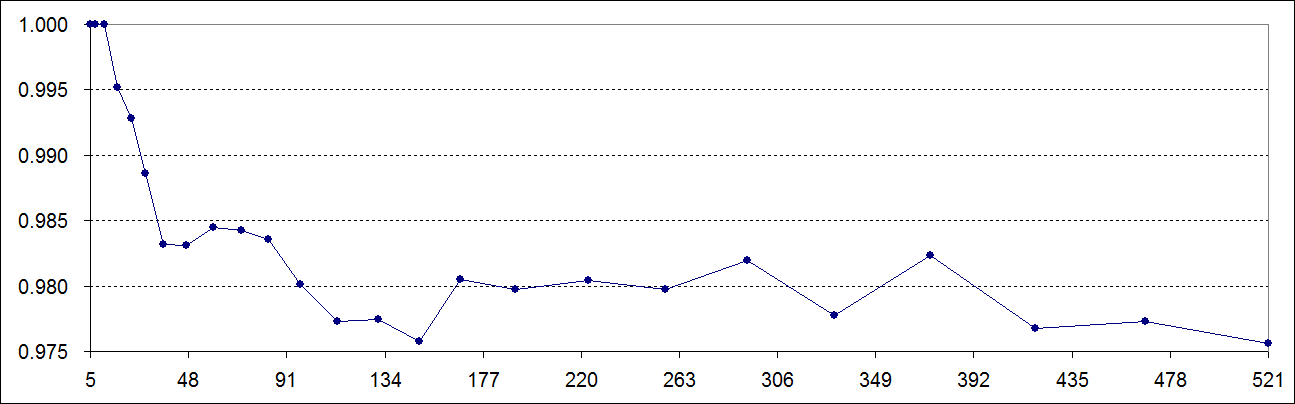
Решения при малых N
Приведём геометрически различные (с точностью до вращений и отражений) полигоны с минимальной и максимальной площадью для первых четырёх задач (N = 5, 7, 11, 17). Уже при при N > 7 полный перебор не реалистичен, поэтому эти варианты являются лучшими в том смысле, что ни кто из участников не нашёл более оптимальных решений. Числа над каждым рисунком означают: N - число точек в полигоне, S - его площадь, и L - периметр. Так, для первой задачи с N = 5 (ниже первые три картинки) минимальная площадь равна 1.5, а максимальная 9. Соответственно "Raw Score" для неё составляет 7.5 (в данном случае это также и "Best Raw Score").
Представление полигона
Первое требование (точки в различных строках и столбцах) выполняется, если полигон описывать следующим образом:
function Polygon(N, n){ this.N = N; // размер сетки и максимум точек в полигоне this.x = new Int16Array(N); // x-координаты точек: 0,1,2,..N-1 this.y = new Int16Array(N); // y-координаты точек: 0,1,2,..N-1 this.n = n !== undefined? n: N; // точек в полигоне (n <= N) this.sqr = 0; // площадь полигона (функция square) this.len = 0; // периметр полигона (функция length) this.par = 0; // число повторных углов сегментов this.val = 0; // ценность в приоритетной очереди} |
Polygon.prototype.init = function(){ for(var k=0; k < this.N; k++) this.x[k] = this.y[k] = k;} |
После инициализации, точки можно случайно перемешать не нарушая первое правило:
Polygon.prototype.mix = function(loops){ while(loops-- > 0){ swap(this.x, rand(0,this.n-1), rand(0,this.n-1)); swap(this.y, rand(0,this.n-1), rand(0,this.n-1)); }} |
var p = new Polygon(5);p.init();for(var i=0; i < 6; i++){ p.mix(10); document.write(p.getSVG(140,140));} |
Случайное перемешивание очень часто приводит к "неправильным" полигонам (не удовлетворяющим второму и третьему требованиям задачи). В этом случае, после параметров полигона над картинкой ставится вопросительный знак. Параметр P означает число совпадающих наклонов.
Пересечение отрезков
Для выявления пересечения двух отрезков будем использовать стандартные геометрические соображения. Пусть один отрезок задан точками b1 и e1 (это векторы), а второй - точками b2 и e2. Отрезки пересекаются, если существует решение параметрического уравнения b1+(e1-b1)t1 = b2+(e2-b2)t2 (в компонентах это система двух уравнений). Параметры t1 и t2 должны находиться в интервале [0,1]. В результате функция, возвращающая true, если отрезки [i1, j1] и [i2, j2] пересекаются, имеет вид:
Polygon.prototype.intersect = function(i1, j1, i2, j2){ var n1X=this.x[j1]-this.x[i1], n2X=this.x[j2]-this.x[i2], bbX=this.x[i2]-this.x[i1]; var n1Y=this.y[j1]-this.y[i1], n2Y=this.y[j2]-this.y[i2], bbY=this.y[i2]-this.y[i1]; var d = n1X*n2Y - n1Y*n2X; if(d===0) // у системы нет решения (параллельны) return false; var t1 = ( bbX*n2Y - bbY*n2X )/d; if(t1 < 0 || t1 > 1) // на прямой вне первого отрезка return false; var t2 = ( bbX*n1Y - bbY*n1X )/d; if(t2 < 0 || t2 > 1) // на прямой вне второго отрезка return false; return true; // отрезки пересекаются} |
Polygon.prototype.conditionIntersect = function(){ for(var i = 0; i < this.n; i++){ // по всем сегментам полигона var num = i? this.n: this.n-1; for(var j = i+2; j < num; j++) // и к ним не примыкающим if(this.intersect(i, (i+1) % this.n, j, (j+1) % this.n) ) return false; // пересечение - условие не выполнено } return true; // условие выполнено} |
Равенство наклонов
При проверке различия наклонов сторон, также используются геометрические соображения. Два вектора параллельны, если их векторное произведение равно нулю:Polygon.prototype.equalSlope = function(i1, j1, i2, j2){ return (this.pntsX[i1]-this.pntsX[j1])*(this.pntsY[i2]-this.pntsY[j2]) === (this.pntsY[i1]-this.pntsY[j1])*(this.pntsX[i2]-this.pntsX[j2]);} |
Polygon.prototype.conditionSlope = function(){ for(var i = 0; i < this.n; i++) for(var j = i+1; j < this.n; j++) if(this.equalSlope(i, (i+1) % this.n, j, (j+1) % this.n) ) return false; return true;} |
Площадь полигона
Площадь полигона, не имеющего самопересечений, вычисляется стандартным образом. Для этого из одной вершины полигона строятся треугольники, основаниями которых являются все не смежные к вершине сегменты:
Polygon.prototype.square = function(){ var s = 0; for(var i1=0; i1 < this.n; i1++){ var i2 = (i1+1) % this.n; s+= (this.x[i1]+this.x[i2])*(this.y[i1]-this.y[i2]); } return this.sqr = s < 0? -s/2: s/2;} |
Случайный поиск
Начнём с самого не эффективного способа решения задачи, а именно будем случайно переставлять координаты точек, пока не получится полигон без пересечений и совпадающих наклонов:
function runRandom(){ var time = new Date(); // время в начале функции do{ for(var it=0; it < 100; it++){ // делаем 100 итераций num1++; polygon.mix(10); // случайно мешаем 10 раз if(polygon.conditionIntersect()){ // проверяем на пересечения num2++; if(polygon.conditionSlope()){ // проверяем на совпадение наклонов num3++; var s = polygon.square(); // вычисляем площадь и ищем мин-макс: if(s < minSqr) { minSqr = s; minSVG = polygon.getSVG(200,200); } if(s > maxSqr) { maxSqr = s; maxSVG = polygon.getSVG(200,200); } } } } } while( new Date() - time < 500); // раз в полсекунды прерываемся setTimeout(runRandom, 100); // пауза 100ms} |
points in polygon N:
Пространство поиска
Пространство состояний в котором ищется решение, зависит от способа его представления. В данной задаче, под состоянием будем понимать конкретное расположение точек и проведенный через них полигон. Далее допустимым состоянием будет считаться замкнутый полигон без пересечений (но возможно с параллельными сторонами), проходящий не через все точки. Финальное состояние - это полигон, проведенный через все точки и удовлетворяющий требованиям задачи (нет пересечений и параллельных сторон). Среди всех финальных состояний необходимо найти оптимальные (в которых площади полигонов минимальны или максимальны).
Пространство состояний в этой задаче очень большое. Действительно, N точек в решётке N x N можно расположить N! способами (все перестановки координаты y, в предположении, что порядок x-ов фиксирован, например по возрастанию). Это число можно уменьшить в 8 раз, отбросив геометрически тождественные расположения (четыре поворота решётки на 90 градусов и для каждого - по два отражения). При данном положении точек существует (N-1)!/2 различных замкнутых путей (см. задачу коммивояжёра).
Таким образом имеется N!(N-1)!/16 полигонов. Требование отсутствия пересечений и различия наклонов сильно уменьшает пространство поиска, оставляя его, тем не менее, слишком большим для полного перебора уже при N > 11.
| N: | 5 | 7 | 11 | 13* | 17 |
|---|---|---|---|---|---|
| N!(N-1)!/16: | 180 | 226800 | 9·1012 | 4·1017 | 5·1026 |
| без пересечений num2/num1 | 21.9% | 3.9% | 0.054% | 0.0042% | 0.000013% |
| и без параллелей num3/num1 | 8.9% | 1.1% | 0.008% | 0.0005% | 0.0000008% |
| num2/num3 | 2.5 | 3.4 | 6.4 | 8.7 | 17.0 |
Организация направленного поиска
Для решения задачи, будем использовать приоритетную очередь, которая каждый раз выдаёт полигон (состояние) с наибольшим значением параметра val (равного, например, площади). Перед началом поиска, в очередь помещаются начальные полигоны, проведенные по n < N точкам. На каждом шаге из очереди извлекается "лучшее" состояние. Оно порождает потомков с числом точек в полигонах n на единицу больше. Для этого одна из не охваченных ещё полигоном точек вставляется между какой-нибудь парой вершин полигона. Когда достигается финальное состояние (n=N), оно запоминается, если его площадь лучше, чем найденная до этого. В противном случае, потомки (все или часть из них) снова помещаются в очередь и процесс повторяется до тех пор, пока очередь open не опустеет.
Приведём в качестве примера процесс построения финального полигона для N = 7 с постепенным добавлением точек, которые приводят к полигону с максимальной площадью:
Поиск реализован в классе PolygonalArea и концептуально имеет следующий вид:
init(); // помещение начальных состояний в очередь openwhile( !open.empty() ) // пока в очереди кто-то есть{ var n = open.shift(); // выталкиваем из неё лучший полигон // и порождаем его наследников: var ix = rand(n.n, N-1); // для этого берём случайный доступный x swap(n.x, n.n, ix); for(var iy=n.n; iy < N; iy++){ // и перебераем все разрешённые y-ки swap(n.y, n.n, iy); for(var i1=0; i1 < n.n; i1++){ // вставляем новую точку в сегмент var i2=(i1+1) % n.n; // между точками с индексами [i1...i2] if(n.notIntersect(n.n, i1,i2) && n.notSlope(n.n, i1,i2)){ var nn = new Polygon(n.N, n.n+1); nn.copyXY(n); // копируем всё из родителя nn.insert(nn.x, n.n, i1); // вставляем новую после точки i1 nn.insert(nn.y, n.n, i1); nn.square(); // вычисляем площадь нового полигона nn.value(); // задаём его ценность if(nn.n === N) // провели полигон через все точки saveBest(nn); // запоминаем лучший, если это он else next.unshift(nn); // добавляем в очередь потомков } } // i1 } // iy while( !next.empty() ) // переносим из очереди потомков в open.unshift( next.shift() ); // общую очередь полигонов} |
Для частично проведенного полигона, x-координаты его n точек находятся в элементах от x[0] до x[n-1]. Поэтому взятие случайного числа в диапазоне [n,...,N-1] (см. строку ix = rand(n.n, N-1)) даёт индекс в массиве координат x для точки, ещё не занятой в полигоне. Это точка переставляется на позицию n (строка swap(n.x, n.n, ix)), откуда она будет вставлена в подходящее место. Возможна также версия алгоритма (более медленная), когда берётся не случайный ix, а перебераются все "свободные" координаты x.
Затем в цикле по iy перебираются все допустимые y-координаты в выбранной колонке x[ix]. Такая точка по-очереди вставляется в каждый сегмент полигона, если это не приводит к пересечениям и равным наклонам. Все полученные полигоны помещаются в приоритетную очередь потомков next, откуда затем переносятся в очередь open. В общем случае в open могут отправляться только несколько лучших потомков.
Проблемы
При организации направленного поиска, следует ответить на вопросы:
1) Выбор стартовых состояний. Процесс поиска должен начинаться с одного или нескольких состояний. В качестве таких состояний используются те или иные незаконченные полигоны, удовлетворяющие критериям задачи. При добавлении точки их площадь может как увеличиваться, так и уменьшаться. Примером стартовых состояний служат все треугольники, вершины которых находятся на крайних вертикальных и нижней линиях сетки:
3) Отбор потомков. В очередь можно помещать не всех потомков данного полигона, а только часть их них (лучшие по некоторому критерию). Это повышает направленность поиска и скорость получения финального состояния. Хотя при этом возможен риск потери перспективных неоконченных полигонов.
4) Критерий направленности. Наиболее важным является выбор условия сортировки приоритетной очереди (задание параметра val). Например, при поиски максимальной площади можно положить val = sqr (в начале очереди находятся полигоны с большим значением val). Впрочем, при добавлении очередной точки, значение площади меняется скачком, поэтому, при сильно незаконченном полигоне (n < N), площадь не является значимым критерием для сортировки. К тому же локальность критерия (оценка по данному незаконченному полигону) может приводить в локальные "овраги" ложных экстремумов.
5) Контроль памяти. Число новых полигонов стремительно растёт и необходимо контролировать размеры очереди. Базовым механизмом является её уполовинивание при достижении длины некоторого предельного значения. Так как для организации приоритетной очереди используется бинарная куча, такой способ постоянно улучшает качество очереди (лучшие значения оказываются вверху кучи). Естественно при этом также могут теряться перспективные состояния.
Эмпирические наблюдения
Приведём некоторые результаты поиска минимальных и максимальных полигонов. Площадь будем измерять в процентах от максимально возможной и равной (N-1)2 для сетки N x N. При больших N относительная минимальная площадь примерно равна 1%, а максимальная 99%:
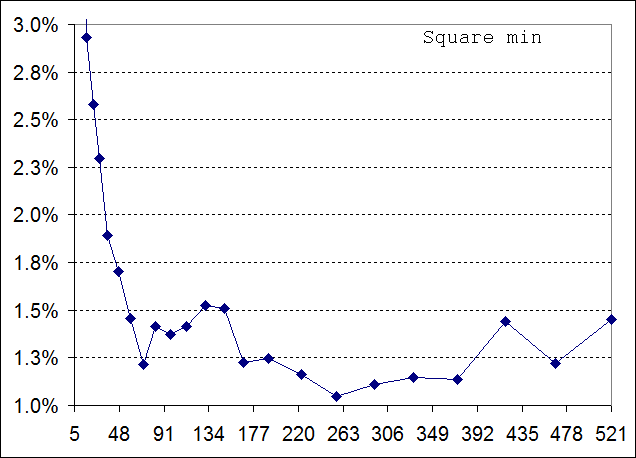
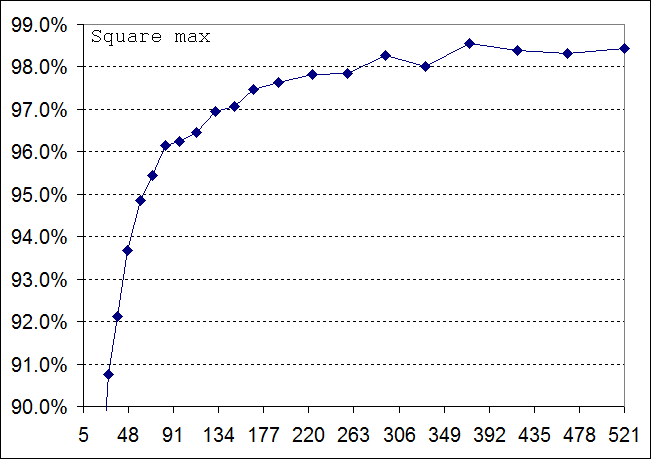
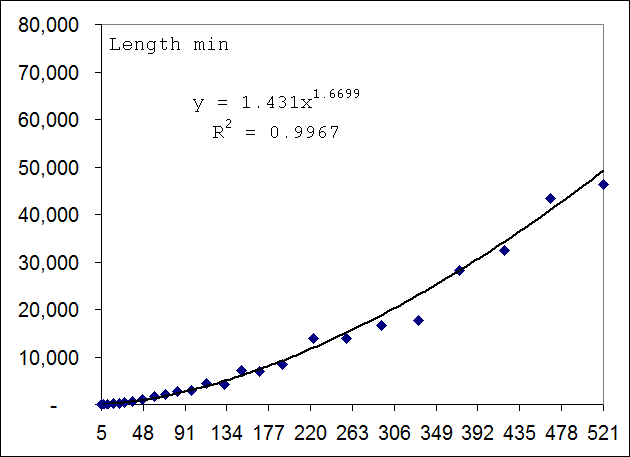
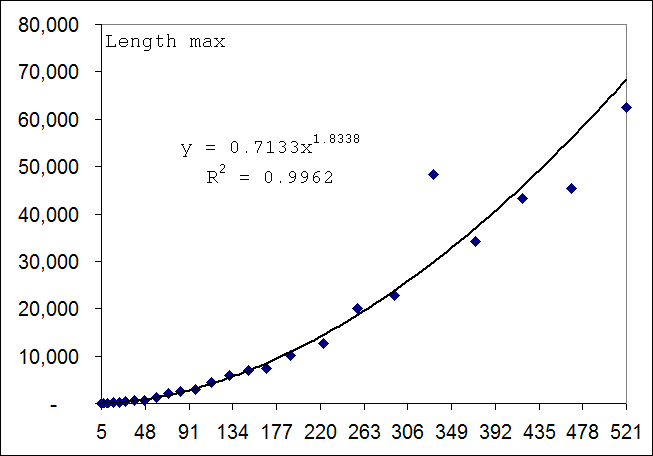
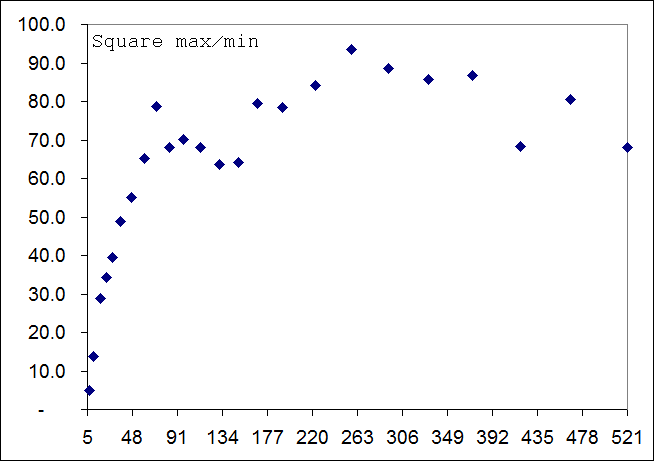
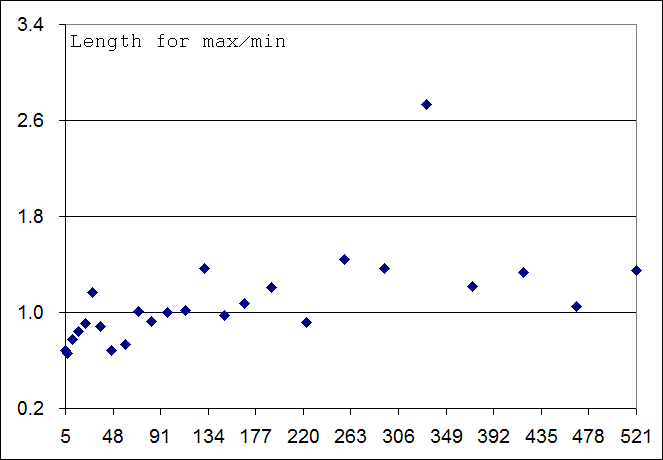
Критерий направленности
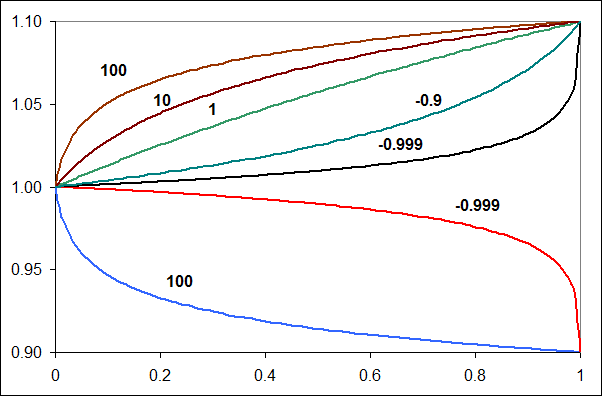При сильно неоконченных полигонах (n << N) необходимо ослаблять роль площади при сортировке в приоритетной очереди.
Для этого площадь (ищем максимум) умножается
на коэффициент, зависящий от отношения x = n/N:
Этот коэффициент определяется двумя параметрами: m - его максимальное отклонение от единицы и a - степень выгнутости. Справа представлены графики k=k(x) для различных m и a. Верхние 5 графиков соответствуют m=1.1, а нижние два - m=0.9. Значения параметра a приведено рядом с кривыми. Чем ближе стремится a к -1 (но не достигает её), тем более плоская получается кривая при малых x. И наоборот, при больших a кривые оказываются более плоскими в окрестности x=1.
Вычисления начинались с сильно выгнутой кривой (a=100) и небольшого m=1.001. Тем самым больший приоритет получали более длинные полигоны при равных площадях. Если очередь застревала (минимальное и максимальное число точек в полигоне долгое время не менялось), то параметр m автоматически немного увеличивался. В результате очередь "подталкивалась" вперёд (к большему числу точек в полигоне).
Аналогичный коэффициент применялся в случае режима допущения параллельных сторон у незаконченных полигонов. В этом случае m < 1 и a < 0. В качестве x выступало отношение par/(N-n+1), где par - число пралелльных сторон (алгоритм порождения новых полигнов не допускал параллельных сторон при par > N-n ).
Начальные состояния максимальной площади
Максимальная площадь оказывается достаточно большая. Если измерять её в процентах от площади сетки (N-1)2, то при N > 100 относительная площадь составляет порядка 98% - 99%.
При поиске полигона с максимальной площадью, стоит начинать с полигонов наибольшей площади, так, чтобы любое добавление в него точек площадь уменьшало. Тогда направленному поиску будет несколько проще. Ниже приведенные полигоны могут только уменьшать площадь при добавлении в них новых точек.
Первая группа полигонов - 4-угольники. В ней первый (не удовлетворяющий критерию параллельности) является верхней возможной границей для максимальной площади:
Ещё одна группа 5-угольников:
и 7-угольников:
Для некоторых больших N площади всех этих стартовых полигонов (в процентах) равны:
| N | 521 | 419 | 293 | 191 | 131 | 97 |
|---|---|---|---|---|---|---|
| S | 99.6 | 99.5 | 99.3 | 99.0 | 98.5 | 97.9 |
Начальные состояния минимальной площади
Минимальная площадь, в процентах достаточно мала (порядка 1%). Кроме треугольников с вершинами на крайних сторонах сетки, используются следующие начальные конфигурации:
Контроль памяти
Для полигона с числом точек n наследников (c n+1 точкой) довольно много (порядка N, не смотря на ограничения!). Поэтому длина приоритетной очереди стремительно растёт. Для контроля памяти, использовался механизм усечения в 2 раза бинарной кучи при достижении её некоторого критического значения. Ниже приведен пример помещения в приоритетную очередь 15 случайных чисел от 0 до 999 (левый рисунок бинарной кучи) и аналогичное помещение (с усечением) 15003 таких же чисел (эта приоритетная очередь выдаёт сначала минимальное число). Видно, что на первых двух уровнях дерева справа более интенсивно скапливаются числа с меньшими значениями. Нижний же (третий) уровень дерева всё время отсекается и наполняется снова (при этом меньшие числа поднимаются вверх):
Для поиска решений, в зависимости от N, использовался размер очереди от 131071 до 16777215 (степень двойки минус один). Каждый полигон имеел в памяти размер около 2*16*N+6*16 байт. Естественно, этот механизм может приводить к потере полигонов, которые в дальнейшем дали бы оптимальное финальное состояние. Но иначе нужна была бы бездонная память.
Ещё один способ борьбы с ростом длины очереди - это жадный алгоритм, когда в очередь помещается только один (лучший) наследник. Впрочем, этот метод не очень хорошо себя зарекомендовал и использовался только при окончании вычислений (когда надоедало ждать обнуления очереди естественным путём). Он же запускался каждую секунду для быстрого получения хоть какого то решения (это для оживления наблюдения за процессом поиска. :)
Обратный поиск
Достаточно эффективным оказался обратный поиск оптимального решения. Для этого брался список лучших полигонов и от них последовательно отрывалось 3, 4, ... худших точек (убирание которых приводило к наибольшему изменению площади в нужную сторону). Затем полученные полигоны помещались в приоритетную очередь и начинался стандартный поиск лучшего решения, путём добавления точек. При отрывании использовался жадный алгоритм (т.е. сначала убиралась одна худшая точка, потом ещё одна и т.д. до нужного числа оторванных точек).
Подбор параметров
Исключаем случайные факторы (нет rX, нет жадного алгоритма (который раз в сек) и фиксированный mN - изменение заависит от времени=загрузки процессора). Нальные полигоны только initLarge5(). На различных длинах очереди (время t очень условно):
N open mN aN max t,s iters sol cnt 23 1023 1.001 100 420.5 420619 33589 (3) 1658 23 2047 1.001 100 427.0 624074 87917 (11) 1394 23 4095 1.001 100 427.5 894611 138166 (1) 1353 23 8191 1.001 100 425.5 757844 582218 (3) 1489 23 16383 1.001 100 427.5 1221137 537380 (9) 941 23 32767 1.001 100 427.5 436 1893722 2407299 (9) 1237 23 32767 1.1 100 425.0 335 1771545 1887887 (2) 796 23 32767 1.1 -0.999 427.5 478 5291325 7319016 (523) 840 23 32767 1.5 100 416.5 178 2165150 3344660 (26) 170 23 32767 1.5 -0.999 413.5 166 4117078 6504699 (647) 141 23 32767 2.0 100 410.5 83 2022860 (26) 87 23 32767 2.0 -0.999 413.5 467 12608101 13522485 (673) 405 23 32767 1.001 100 427.5 436 1893722 2407299 (9) 1237 23 32767 1.001 100 418.5 66 1572479 732241 (1) 128 rX=true 23 32767 1.001 100 420.5 77 1627452 1068612 (1) 145 rX=true 23 32767 1.001 100 420.5 80 1428195 1221021 (1) 143 rX=true 23 32767 1.001 100 420.5 81 1516386 913224 (1) 157 rX=true 23 32767 1.001 100 417.5 81 1938920 1140675 (4) 145 rX=true 23 32767 1.001 100 419.0 87 1265928 1150768 (2) 142 rX=true!!!