Вероятностные методы

---

Введение

Иногда обучающих примеров одного класса существенно больше чем других. В этом случае необходимо корректно вычислять ошибку классификации. Иначе правило: [любой объект принадлежит "большому" классу] будет давать "неплохие" результаты в процентах ошибок. Но это, конечно, не то, что ожидают от распознающей системы. Если же искусственно выравнять число обучающих примеров различных классов, мы потеряем важную эмпирическую информацию о частоте появления объектов.

---

Априорные и апостериорные вероятности

Пусть есть большое, "случайно перемешанное" обучающее множество из $N$ объектов. Объектов первого класса в нём $N_1$ штук, второго - $N_2$ штук и т.д.: $$N=\sum N_k.$$ Вероятность того, что случайно выбранный их множества объект принадлежит $k$-тому классу равна: $$P(k) = \frac{N_k}{N}.$$

Рассмотрим маленький объём $V$, окружающий точку $\mathbf{x}$ в пространстве признаков. Посчитаем сколько объектов $N(\mathbf{x})$ в него попало. Аналогично, обозначим через $N_k(\mathbf{x})$ - число объектов $k$-того класса в этом объёме.
Условная вероятность того, что объект в объёме $V$, имеющий признаки $\mathbf{x}$, принадлежит $k$-тому классу, равна: $$P(k|\mathbf{x}) = \frac{N_k(\mathbf{x})}{N(\mathbf{x})}.$$

Вероятности $P(k)$ называют априорными, в том смысле что они нам известны и, не глядя на вектор признаков данного объекта, можно утверждать, что он принадлежит $k$-тому классу с вероятностью $P(k)$. В тоже время $P(k|\mathbf{x})$ это уже апостериорная вероятность, которая меняет значение $P(k)$ после того, как мы "посмотрели" на вектор $\mathbf{x}$ признаков объекта. Именно эти вероятности нас интересуют в задаче классификации.

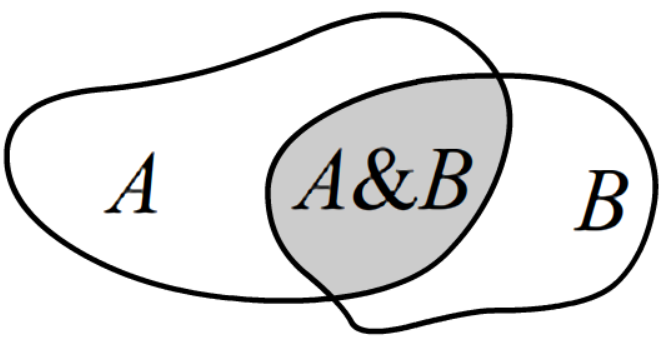В общем случае, в теории вероятностей, условная вероятность наступления события $A$, если известно, что произошло событие $B$, определяется следующим образом: $$P(A|B)= \frac{P(A,B)}{P(B)},$$ где $P(A,B)$ - совместная вероятность (доля событий при которых произошло и $A$ и $B$: на рисунке закрашенная область), а $P(B)$ - вероятность событий $B$ (когда происходило $B$ и что угодно ещё).

---

Плотности распределения вероятностей

Условная плотность вероятностей того, что объект $k$-того класса находится в объёме $V$ равна: $$p(\mathbf{x}|k) ~=~ \frac{N_k(\mathbf{x})/V}{N_k} ~=~ \frac{n(\mathbf{x})}{N_k},$$ где $n(\mathbf{x})$ - концентрация объектов $k$-того класса ( = плотность их числа = число в единице объёма). Слово 'плотность' означает, что мы относим вероятность в объёме к величине этого объёма. Соответственно, суммарная вероятность по всем небольшим объёмам равна единице: $$\int p(\mathbf{x}|k)\,d^n\mathbf{x} = \frac{1}{N_k}\,\int n(\mathbf{x}|k)\,d^n\mathbf{x} = \frac{N_k}{N_k} = 1.$$ Плотности вероятности далее обозначаются прописным шрифтом, а просто вероятности - заглавным.

Совместная плотность вероятности $p(\mathbf{x},k)$ того, что случайно выбранный из объёма $V$ объект принадлежит классу $k$, равна: $$p(\mathbf{x},k) = \frac{N_k(\mathbf{x})/V}{N}=\frac{n_k(\mathbf{x})}{N},~~~~~~~~~~~~~~~~~p(\mathbf{x})=\frac{N(\mathbf{x})/V}{N}=\frac{n(\mathbf{x})}{N}.$$ Соответственно, $p(\mathbf{x})$ - плотность вероятности обнаружить в объёме объект любого класса.

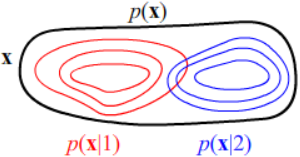На рисунке справа, при помощи карты высот, красными линиями обозначена плотность распределения вероятностей объектов первого класса $p(\mathbf{x}|1)$, а синие линии - плотность распределения объектов второго класса $p(\mathbf{x}|2)$. Это два холмика с не совпадающими вершинами. В окрестности этих вершин концентрации объектов $n_k(\mathbf{x})$ соответствующих классов максимальны. Если бы мы не учитывали класс объекта, получилась бы некоторая безусловная плотность вероятностей $p(\mathbf{x})$ или концентрация объектов (любых) $n(\mathbf{x})$.

---

Формула Байеса

Из данных определений непосредственно следуют нормировочные условия: $$\sum_k P(k) = 1,~~~~~~~~~~~\sum_k p(\mathbf{x},k) = p(\mathbf{x}),~~~~~~~~~~~~~~\int p(\mathbf{x},k)\,d^n\mathbf{x}=P(k),~~~~~~~~~~\int p(\mathbf{x})\,d^n\mathbf{x} = 1.$$ Кроме этого справедливо соотношение, называемое формулой Байеса: $$P(k|\mathbf{x}) = \frac{p(\mathbf{x}, k)}{p(\mathbf{x})} = \frac{p(\mathbf{x}|k)\,P(k)}{p(\mathbf{x})} = \frac{n_k(\mathbf{x})}{n(\mathbf{x})},$$ Отметим также очевидное нормировочное условие: $$\sum_k P(k|\mathbf{x}) = 1,~~~~~~~при~любом~\mathbf{x}.$$ Оно означает, что объект с признаками $\mathbf{x}$ хоть какому-то классу, да принадлежит.

---

Разделяющая поверхность

Пусть есть только два класса. Разделяющую их поверхность построим, считая что на ней вероятности обоих классов равны: $P(1|\mathbf{x})=P(2|\mathbf{x})$ или по формуле Байеса: $$P(\mathbf{x}|1)\,P(1) = P(\mathbf{x}|2)\,P(2)~~~~~~~\Leftrightarrow~~~~~~~~n_1(\mathbf{x})=n_2(\mathbf{x}).$$ Равенство условных вероятностей $P(k|\mathbf{x})$ эквивалентно равенству концентраций объектов. Поэтому байесовское правило классификации утверждает, что

на разделяющей поверхности концентрации объектов обоих классов должны совпадать.

Распределения $P(k)$ и $p(\mathbf{x}|k)$ строят по обучающему множеству объектов. При этом непрерывная функция $p(\mathbf{x}|k)$ аппроксимируется тем или иным параметрическим распределением вероятности (например, многомерным распределением Гаусса). Параметры этого распределения подгоняются под обучающие данные. Можно также сглаживать гистограмму распределения и т.д. (см. ниже).

---

Нормальное распределение

В качестве простого примера рассмотрим симметричные гауссовы (=нормальные) распределения вероятностей признаков $\mathbf{x}$ объектов двух классов ($k=1,2$) вокруг центров $\mathbf{c}_1$ и $\mathbf{c}_2$: $$p(\mathbf{x}|k) = \frac{1}{(2\pi)^{n/2}\,\sigma^n_k}\,\exp\Bigr\{-\frac{(\mathbf{x}-\mathbf{c}_k)^2}{2\,\sigma^2_k}\Bigr\}.$$ В одномерном случае это распределение приведено ниже на первом рисунке ($\sigma=1$), а при $n=2$ в виде карты высот на втором. На третьем - в плоскости создано 1000 точек в соответствии с нормальным распределением:

Беря натуральный логарифм от уравнения разделяющей поверхности $P(\mathbf{x}|1)\,P(1)=P(\mathbf{x}|2)\,P(2)$, получаем: $$\frac{(\mathbf{x}-\mathbf{c}_1)^2}{\sigma^2_1} + 2\,\ln \frac{\sigma^{n}_1}{P(1)} = \frac{(\mathbf{x}-\mathbf{c}_2)^2}{\sigma^2_2} + 2\,\ln \frac{\sigma^{n}_2}{P(2)}.$$ Волотильность $\sigma_k$ характеризует характерный радиус $k$-того класса. Поэтому это уравнение похоже на меру $d(\mathbf{x},\mathbf{c})/R=\min$ с евклидовым расстоянием в $n$-мерном пространстве. Однако оно отличается дополнительными слагаемыми, зависящими от $\sigma_k$ и $P(k)$. Ожидаемо, разделяющая поверхность "отталкивается" от класса с большей вероятностью $P(k)$. А вот логарифмическое слагаемое с $\sigma_k$ более необычное. При больших размерностях пространства $n$ оно даёт заметный вклад. Ниже приведены соответствующие разделяющие поверхности для $\sigma_1/\sigma_2=2$ и различных $n$ (сечение $n$-мерного пространства 2-мерной плоскостью, проходящей через центры $\mathbf{c}_1$, $\mathbf{c}_2$; первый рисунок не учитывает логарифмические вклады и $P(1)=P(2)$):

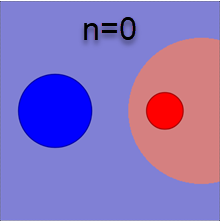
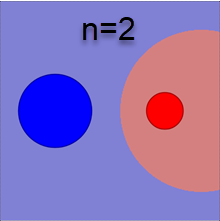
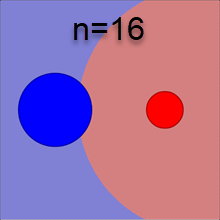
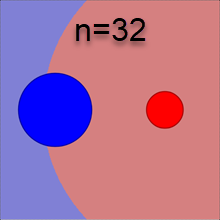
Кажется неожиданным, что более компактное гауссово облако отодвигает от себя границу между классами тем сильнее, чем больше размерность пространства. Этот эффект является ещё одним парадоксальным свойством многомерного пространства.

---

Парадоксы $n$-мерного Гаусса

Чтобы разобраться с этим эффектом, запишем симметричное распределение Гаусса с центром в начале координат, в сферических координатах ($\sigma=1$): $$p(r) = \frac{e^{-r^2/2}}{(2\pi)^{n/2}}\,r^{n-1}\,\Omega_n,~~~~~~~~~~~~\Omega_n=\frac{2\,\pi^{n/2}}{\Gamma(n/2)},$$ где $\Omega_n$ - $n$-мерный телесный угл. Ниже на первом рисунке приведены графики этого распределения при различных $n$. На втором - интегралы распределения от 0 до $r$:

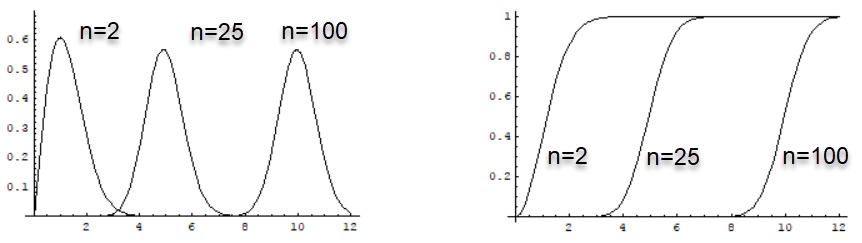
Вычислим также среднее расстояние объекта: $$\langle r^m \rangle = \int p(\mathbf{x}|k)\, r^m\,d^n\mathbf{x} = 2^{m/2}\,\frac{\Gamma((n+m)/2)}{\Gamma(n/2)}.$$

При больших $n$ и $m=1$ это соотношение имеет асимптотическое поведение: $\langle r\rangle \approx \sqrt{n}$. Таким образом, среднее расстояние объектов от центра растёт с ростом размерности пространства. В тоже время, среднеквадратичное отклонение $\langle (r-\langle r \rangle)^2 \rangle^{1/2}\approx 0.7$ и очень слабо зависит от $n$. Другим словами, когда $\sigma\neq 1$, практически любой объект "гауссового облака" будет находиться в узком сферическом слое радиуса $\sigma\sqrt{n}$, что при больших $n$ существенно больше $\sigma$.

Рассмотрим два класса с различными центрами и $\sigma_1=2$, $\sigma_2=1$. Пусть число объектов в каждом классе одинаково, т.е. $P(1)=P(2)$. Отношение площадей сфер классов будет равно $2^{n-1}$ (площадь сферы радиуса $R$ пропорционально $R^{n-1}$). А отношение объёмов сферических слоёв, где в основном сосредоточены объекты, равно $2^n$ (характерная толщина слоя первого класса также в 2 раза больше). При этом число объектов обоих классов одинаково. Следовательно, плотность в единице объёма объектов первого класса (с большей сигмой) будет в $2^n$ раз меньше чем у второго. Этот же факт можно вывести и из нормировочного множителя $1/\sigma^n_k$ плотности $p(\mathbf{x}|k)$.

Любопытно, что при проектировании $n$-мерного распределения на 2D-плоскость увидеть "кольцо" $n$-мерной сферы, где расположены объекты нельзя (даже, если отбирать только близкие к плоскости объекты). Плотность точек в центре по-прежнему будут выше, аналогично 2-мерному случаю. Дело в том, что шар радиуса $R$ в $n$-мерном пространстве имеет существенно меньший объём, чем сферический слой радиуса $R$ и шириной $\Delta R$ (отношение объёма сферического слоя к объёму шара $\Delta V/V = 1-(1-\Delta R/R)^n$ быстро стремится к единице). Однако, при проектировании на плоскость, шар переходит в 2-мерный круг, площадь которого больше, чем площадь в кольца той-же ширины $\Delta R$. Поэтому внутри круга наблюдается повышенная концентрация объектов из-за искажения масштабов при проектировании на плоскость.

---

Численный эксперимент

Возьмём две n-мерные гауссианы на расстоянии 10. У одной $\sigma_1=2$ (первый класс), а у второй - $\sigma_2=1$ (второй класс). Создадим по 10000 объектов в каждом классе и вычислим ошибку классификации методом 1-NN (ближайшего соседа) при помощи leave-one-out методики:

n	2	16	25	36	49	64	81	100	144
err	0.05%	0.20%	0.53%	1.78%	5.74%	14.1%	28.1%	41.4%	49.6%

Видно, что ошибка растёт с ростом размерности пространства. При этом ошибочно, практически всегда классифицируется первый класс (с большей $\sigma$). При $n=144$ он классифицируется полностью неверно (всегда принимается за второй класс). Связано это с тем, что ближайший сосед чаще оказывается из второго класса, имеющего большую плотность на сфере.

Более того, объекты первого класса на столько сильно "размазаны" по поверхности $n$-мерной сферы, что их расстояние к ближайшему соседу своего класса на сфере при $n=100$ в среднем больше ($\approx 22$), чем радиус этой сферы ($\approx 20$)! К тому же в 100-мерном пространстве сфера второго класса оказывается внутри сферы первого класса ($R_1\approx 20$, $R_2\approx 10$ а расстояние между центрами $10$). Поэтому к любому объекту первого класса ближе находится объекты второго класса (но не наоборот!).

Хотя метод ближайшего соседа "буксует" при больших $n$, правило $$k = \arg\min_k \Bigr\{\frac{(\mathbf{x}-\mathbf{c}_k)}{\sigma^2_k} + 2n\ln\sigma_k\Bigr\},$$ приводит к нулевой ошибке (при $n=100$). При этом более простое классификационное правило $k=\arg\min_k(\mathbf{x}-\mathbf{c}_k)^2$ даёт небольшую ошибку $0.25%$ при $n=100$, в то время как правило $k=\arg\min_k(\mathbf{x}-\mathbf{c}_k)^2/\sigma^2_k$, как и метод 1-NN, не работает.

---

Произвольное нормальное распределение

В общем случае нормальное распределение с произвольными дисперсиями и ковариационной матрицей $\mathbf{C}_k$ для $k$-того класса имеет вид: $$p(\mathbf{x}|k) = \frac{1}{\sqrt{(2\pi)^n\,\det \mathbf{C}_k}}\,\exp \Bigr\{-\frac{1}{2}\,(\mathbf{x}-\bar{\mathbf{x}}_k)\cdot\mathbf{C}^{-1}_k\cdot(\mathbf{x}-\bar{\mathbf{x}}_k)\Bigr\}.$$ Разделяющая поверхность между классами строится по принципу равенства расстояний между классами: $$d^2_k(\mathbf{x}) = (\mathbf{x}-\bar{\mathbf{x}}_k)\cdot\mathbf{C}^{-1}_k\cdot(\mathbf{x}-\bar{\mathbf{x}}_k) + \ln \det \mathbf{C}_k - 2\ln P(k).$$ Первое слагаемое является квадратом расстояния Махаланобиса, использующееся при работе с эллиптическими эталонами. Второе слагаемое - поправка на многомерие, а третье - на неравенство объектов различных классов.

---

Параметрические методы

При использовании байесовского классификатора необходимо уметь оценивать вероятности классов $P(k)$ и плотности вероятностей $p(\mathbf{x}|k)$ вектора $\mathbf{x}$ признаков $k$-того класса. Если обучающее множество не искажено и в тестовом множестве (или при применении на практике) объекты различных классов будут появляться с той же частотой, то можно положить $P(k)=N_k/N$, где $N_k$ - число объектов класса $k$ в обучающей выборке из $N$ объектов.

Методы оценки плотностей $p(\mathbf{x})$ (номер класса опускаем) можно условно разделить на параметрические и непараметрические.

В параметрических методах плотность вероятности $p(\mathbf{x})$ аппроксимируют некоторой известной функцией $p(\mathbf{x})= f(\mathbf{x},\theta)$ (например, нормальным распределением). Эта функция зависит от набора параметров $\theta$ (различных для разных классов). Параметры подбираются так, чтобы плотность вероятности наилучшим образом описывала эмпирическое распределение объектов. Для нормального распределения это будет центр масс объектов (средний вектор признаков) и ковариационная матрица.

Обобщение этой идеи состоит в рассмотрении смеси распределений: $$p(\mathbf{x})= \sum_i \omega_i\,f_i(\mathbf{x},\theta_{i}),$$ где $f_i$ - опять же известные функции просуммированные с некоторыми весами $\omega_i$ (которые, как и параметры $\theta_{i}$, необходимо подобрать).

Многомерная функция плотности сильно упрощается, если признаки статистически не зависимы. Тогда: $$p(\mathbf{x})=p_1(x_1)\,p_2(x_2)\,...\,p_n(x_n).$$ В этом случае можно решать $n$ более простых задача оценки плотностей вероятностей одномерных случайных величин. Каждую функцию $p_i(x_i)$ можно оценивать как параметрическими, так и непараметрическими методами. Не смотря на то, что на практике статистическая независимость, обычно, не выполняется, такая "наивная" факторизация многомерной функции $p(\mathbf{x})$ часто неплохо работает.

---

Непараметрические методы

При непараметрической оценке плотности вероятности, тем или иным способом строят гистограмму распределения. Начнём с одномерного случая. Возьмём все объектов обучающей выборки (данного класса), которые попали в интервал $[x-h, x+h]$, где $h$-некоторый параметр и разделим на ширину интервала $2h$, которая называется окном, а также на число объектов. Это и будет плотность вероятности. Формально её можно записать следующим образом: $$p(x) = \frac{1}{N}\,\frac{1}{V}\sum^N_{i=1} K(x-x_i),~~~~~~~~~~~V = \int K(x)\,dx,$$

где $K(x)$ - ступенчатая функция, равная $1$, если $|x|\lt h$ и нулю в противном случае. Площадь такой ступеньки равна $V=2\,h$.

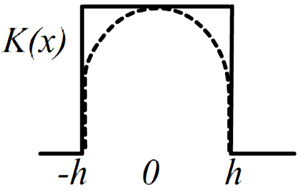Можно обобщить эту идею, взяв вместо ступеньки некоторую гладкую функцию, которую называют ядром. Её интеграл по всему диапазону изменения $x$ равен $V$. Несложно проверить, что нормировка плотности вероятности при этом сохраняется: $$\int p(x)\,dx = \frac{1}{N}\,\frac{1}{V}\sum^N_{i=1} \int K(x-x_i)\,dx = \frac{1}{N}\,\frac{1}{V}\sum^N_{i=1} V = 1.$$ Подобный метод называется оценкой Парзена-Розенблатта. В качестве ядра $K(x)$, обычно, выбирают симметричные функции с максимумом при $x=0$. Чем медленнее убывает ядро, тем более сглаженной получается гистограмма.

В $n$-мерном случае в качестве ядра можно брать произведение одномерных ядер $K_1(x_1)\cdot...\cdot K_n(x_n)$. Они могут быть одинаковыми или разными. Другой способ - брать симметричную функцию $K(|\mathbf{x}-\mathbf{x}_i|)$. В любом случае, полученную плотность необходимо делить на объём, равный интегралу от ядра по всему пространству.

Существуют варианты метода с переменным окном. Пусть ядро является кусочно гладкой функцией типа $(1-(x/h)^2)$ при $x \le h$ и $0$ вне окна ($V=4h/3$). В этом случае, для каждого $\mathbf{x}$ можно выбрать различные $h$ так, чтобы в окно попало $k$ объектов. Тогда в областях где объектов мало, сглаживание распределения будет производится широким окном, а там где много - узким. При принятии решения о ширине окна необходимо использовать не объекты данного класса, а объекты всех классов в обучающей выборке.

---

Цена ошибки

При классификации объектов различают ошибки первого и второго рода. Рассмотрим гипотезу: $H=$"объект $\mathbf{x}~\in$ классу $A$". При этом пусть класс $A$ более ожидаем (например "человек здоров" или "в помещении нет задымления").

• Ошибка 1-го рода (ложное срабатывание) возникает, когда $H$ неверно отвергнута.
• Ошибка 2-го рода (пропуск события) – $H$ неверно принята.

Рассмотрим пример с одним признаком $x$ который является диагностическим параметром при выявлении болезни. Левая таблица в числе людей, а правая - вероятности:

x:	1	2	3	4	5	всего
$N_1(x)$ здоровых:	5	20	50	20	5	100
$N_2(x)$ больных:	0	2	4	8	6	20

x:	1	2	3	4	5	всего
$P(x|1)$:	0.05	0.20	0.50	0.20	0.05	P(1)=100/120
$P(x|2)$:	0.00	0.10	0.20	0.40	0.30	P(2)=20/120

Найдём разделяющую поверхность.Так как равенство $P(x|1)P(1)=P(x|2)P(2)$ эквивалентно $N_1(x)=N_2(x)$, получаем $x\sim 5$. Такая граница выглядит завышенной, так как она не соответствует максимуму распределения вероятностей больных. Понятно, что в данной задаче важнее не пропустить болезнь. Выход - учитывать стоимость ошибочных классификаций.

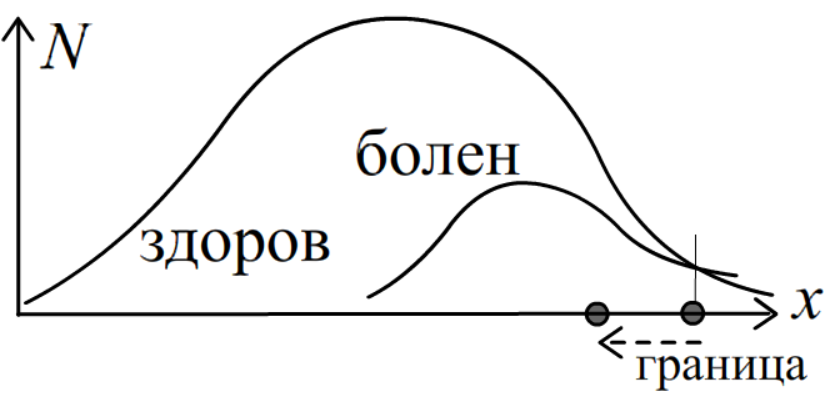Для этого вводится $c_{k,q}$ - цена неправильного отнесения объекта класса $k$ к классу $q$. В примере выше имеет смысл положить: $$c_{болен,здоров} \gt c_{здоров,болен}.$$ Пусть между классами в пространстве признаков проведены разделяющие поверхности, которые делят всё пространство на объёмы $V_1$,...,$V_K$, где $k$-й класс занимает объём $V_k$. Вероятность $P_{kq}$ отнести объект $k$-того класса к классу $q$ равна: $$P_{kq} = \int\limits_{V_q} p(\mathbf{x},k)\,d^n\mathbf{x}.$$ Средние потери (функция стоимости) отнесения объекта класса $k$ к любому другому классу: $$\mathrm{Cost}(k) = \sum_{q} c_{kq}\,P_{kq}.$$ Суммарные средние потери по всем классам должны быть минимальными: $$\mathrm{Cost} = \sum_k\mathrm{Cost}(k) = \sum_{k,q} c_{kq}\, P_{kq} = \min.$$ Границей между двумя классами будет: $$\mathrm{Cost}(k) = \mathrm{Cost}(q).$$ В примере выше, при $c_{болен,здоров} \gt c_{здоров,болен}$, граница между классами здоров-болен сдвинется от отметки $x\approx 5$ влево, давая большее срабатывание на потенциальных больных (уменьшение ошибок второго рода).

Понятно, что при правильной классификации потерь нет: $c_{kk}=0$. Обычно также справедливо $c_{kq}=c_k$ - т.е. не важно к какому классу ошибочно отнесли $k$-тый класс (потеря ошибки этого класса одна и та же). В этом случае классификационный алгоритм имеет вид: $$k = \arg\max_k \,c_k\,\, p(\mathbf{x}|k)\,P(k) = \arg\max_k \,c_k\,n_k(\mathbf{x}),$$ где, как и выше, $n_k(\mathbf{x})$ - плотность числа объектов класса $k$. Для двух классов уравнение разделяющей границы имеет вид: $$c_{1}\,p(\mathbf{x}|1)\,P(1) = c_2\,p(\mathbf{x}|2)\,P(2).$$

---

Полезная информация

• Пугачев В.С. - "Теория вероятностей и математическая статистика" (2002)
• Воронцов К.В. - "Лекции по статистическим" (байесовским) алгоритмам классификации (2008)
• Мерков А.Б - "Распознавание образов: Построение и обучение вероятностных моделей" (2014)
• Отрывок из семинара

---