Расстояние и близость
Введение
В задачах распознавания или кластеризации ключевую роль играет выбор набора признаков, описания объекта. Если число признаков равно n, то говорят об n-мерном пространстве признаков. Каждый объект является точкой такого пространства с координатами x={x1,...,xn}. При удачном выборе признаков, похожие (например, с человеческой точки зрения) объекты обычно находятся близко. Соответственно, необходим некоторый критерий близости или расстояния.
Метрическое пространство
Пусть расстояние d между точками a и b в n-мерном пространстве неотрицательно, равно нулю для совпадающих точек (и только для них), а также симметрично: d(a,b)≥0, d(a,a)=0 d(a,b)=d(b,a). Кроме этого, путь оно (как и в евклидово расстояние) удовлетворяет неравенству треугольника: d(a,b)+d(b,c)≥d(a,c). Пространство, в котором задано расстояние между двумя точками, удовлетворяющее этим аксиомом, называется метрическим.
Евклидово расстояние и нормализация
Наиболее популярным и привычным является евклидово расстояние: d(a,b)=√(a−b)2=√(a1−b1)2+...+(an−bn)2 Его использование предполагает, что все компоненты вектора признаков имеют равную дисперсию, независимы и одинаково важны при классификации объектов (дают равный вклад в расстояние между объектами).
Поэтому, обычно, вычисляют среднее значение (центр тяжести) вектора признаков и дисперсию каждого признака (корень из неё называется волатильностью σi=√Di): ˉx≡⟨x⟩=1NN∑μ=1xμ, σ2i=Di=⟨(xi−ˉxi)2⟩=1N−1N∑μ=1(xμi−ˉxi)2, где xμi - i-тый признак μ-того объекта. Затем векторы признаков нормализируют. Возможны различные способы нормализации: x′i=xi−minimaxi−mini, x′i=xi−ˉxiσi. Первый способ чувствителен к одиночным "выбросам", поэтому чаще используют деление на волатильность (второй способ) Для нейронных сетей лучше подходит следующая нормировка: x′i=S(xi−ˉxiσi), где S(d)=1/(1+exp(−d)) - сигмоидная функция, гарантирующая что признак будет находиться в интервале [0...1].
Расстояния между рукописными цифрами
Рассмотрим в качестве примера евклидовы расстояния между рукописными цифрами, представленными растровыми изображениями 28 на 28 пикселей в градациях серого. При этом белый цвет (фон) соответствует нулевому значению пикселя, а чёрный цвет равен единице. Пространство признаков имеет 28*28=784 измерения.
Ниже приведены средние значения по 60000 обучающим примерам базы MNIST после устранения скоса изображений. В каждой строке дана цифра от 0 до 9 и справа от неё, в порядке увеличения расстояния, другие цифры (евклидово расстояние снизу после двоеточия), а также белый и чёрный фон:

av si min max aver sigma min max 0 5.4 1.1 2.1 9.7 1 2.2 1.0 0.6 9.1 2 5.9 0.8 3.5 9.2 3 5.4 0.9 2.5 9.4 4 5.0 0.9 2.6 10.3 5 5.5 0.9 2.8 9.5 6 5.1 1.0 3.0 10.3 7 4.6 1.0 2.4 10.4 8 5.2 1.0 2.9 10.1 9 4.6 1.1 2.5 10.3
Максимальное расстояние в таком пространстве признаков равно 28 (это расстоятние между белым и чёрным фоном). Из матрицы расстояний следует близость между собой цифр (3,5,8) и (4,9,7). Цифры 0 и 1 наиболее различимы (удалены на максимальное расстояние). Однако в целом разброс расстояний между изображениями не велик. Справа от матрицы расстояний приведены статистики расстояний отдельных цифр базы MNIST от своих средних значений. Как видно, цифры откланяются от усреднённого образа достаточно сильно (сравнимо с расстояниями между образами различных классов).
Естественно, набор пикселей - это не лучший вариант вектора признаков. Например, различные написания единицы достаточно далеко отстоят друг от друга в пространстве признаков:
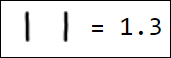 | 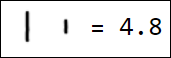 | 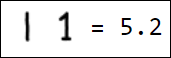 | 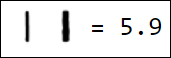 | 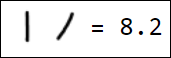 |
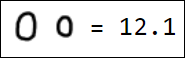 | 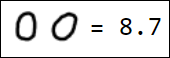 | 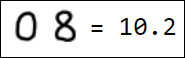 | 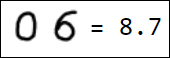 | 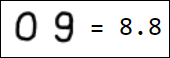 |
Расстояние Махаланобиса
Если есть заметное различие в дисперсии или статистическая зависимость признаков, иногда используют расстояние Махаланобиса: d2(a,b)=∑i,j(ai−bi)C−1ij(aj−bj), где C−1ij - матрица, обратная к ковариационной матрице Cij=⟨(xi−ˉxi)(xj−ˉxj)⟩ и фигурные скобки означают усреднение по всем объектам. Если координаты вектора признаков между собой статистически не связаны, то C−1ij диагональна δij/Di, где Di - дисперсии признаков xi. В этом случае, в расстоянии Махаланобиса происходит деление компонент векторов на их дисперсию. Тем самым выравнивается значимость их вклада в суммарное расстояние.
Отметим, что расстояние Махаланобиса инвариантно относительно линейного преобразования. Действительно, при таком преобразовании меняется ковариационная матрица: x′i=n∑k=1Rikxk ≡ (Rx)i, C′ij=⟨(x′i−ˉx′i)(x′j−ˉx′j)⟩=∑k,pRikRjpCkp=(RCRT)ij. Соответственно: d(a′,b′)=(a′−b′)TC′−1(a′−b′)=(a−b)TRT(RCRT)−1R(a−b)=(a−b)TC(a−b)=d(a,b).
Вместо использования расстояния Махаланобиса, можно один раз произвести линейное преобразование пространства признаков, так чтобы x′=Rx RCRT = 1. В результате такого преобразования корреляция признаков устраняется и их дисперсии становится единичной. Впрочем, устранение корреляции признаков для всех классов не всегда разумно и может ухудшить их разделимость.
Расстояние Махаланобиса можно также использовать как меру близости к конкретному кластеру объектов (данного класса), если этот кластер имеет эллипсоидальную форму. При этом ковариационная матрица должна быть вычислена, естественно, только по объектам входящим в кластер.
Другие функции расстояния
Манхетенское расстояние: d(a,b)=∑i|ai−bi| Расстояние максимума: d(a,b)=max(|ai−bi|)
Иногда значимо не абсолютное положение объекта в пространстве признаков, а единичный вектор, направленный из начала координат в сторону объекта. Тогда в качестве меры близости используют косинус между векторами: d(a,b)=1−ab|a||b|, где ab=a1b1+...+anbn - обычное евклидово скалярное произведение векторов, а |a| - длина вектора.
Если все признаки положительны и векторы объектов нормированы на единицу, может оказаться полезным расстояние Кульбака — Лейблера: d(a,b)=n∑i=1ailnaibi, ai,bi≥0, n∑i=1ai=n∑i=1bi=1. Эта функция расстояния не метрическая, так как не симметрична и не удовлетворяет неравенству треугольника. Тем не менее расстояние Кульбака — Лейблера минимально (и равно нулю), когда компоненты единичных векторов совпадают. Можно использовать также и его симметризованную версию d(a,b)+d(b,a).
Взвешенное расстояние Минковского
Даже если дисперсия различных признаков одинакова, при помощи весовых коэффициентов ωi можно учитывать важность признаков для задачи классификации: d(a,b)=(n∑i=1ωi(ai−bi)p)1/p Если все ωi=1 и p=2, мы возвращаемся к евклидовму расстоянию.
Близость
По-мимо расстояния иногда рассматривают понятие близости или сходства s, удовлетворяющее более слабым аксиомам: 0≤s(a,b)≤1, s(a,a)=1, s(a,b)=s(b,a). Например, если компоненты вектора признаков x принимают только значения 0 или 1 (бинарные признаки), то можно определить следующие функции сходства: s(a,b)=N11(a,b)n, s(a,b)=N11(a,b)+N00(a,b)n, s(a,b)=N11(a,b)N11(a,b)+N10(a,b)+N01(a,b), где N11(a,b) - число совпадающих единичных признаков, N00(a,b) - совпадающих нулей, а N10(a,b) - число координат равных 1 в a и 0 в b (аналогично N01).