Нейронные сети: 2. Разделяющие поверхности
Введение
В предыдущем документе была рассмотрена геометрическая интерпретация нейрона, как вычислителя нормированного расстояния от вектора, подаваемого на его вход, к гиперплоскости, ориентация и положение которой определяется параметрами нейрона (w0,w1,...,wn). Выход нейрона будет больше 0.5, если вход лежит по вектору нормали ω={w1,...,wn} к гиперплоскости и меньше 0.5, если против.
Если гиперплоскость нейрона c n входами отсекает один из углов n-мерного гиперкуба, то такой нейрон работает как логический элемент. Когда его вектор нормали направлен в этот угол (меньший объём пространства), то это логическое "И" входных значений (или их отрицаний), а если в противоположную сторону (в больший объём), то это логическое "ИЛИ". Таким образом, нейронная сеть может вычислять любую логическую функцию. Подбором уверенности нейрона можно получить как стандартные булевы результаты, так и вычисления в рамках нечёткой логики.
В этом документе, на примере 2-мерного пространства признаков, изучается как нейронная сеть справляется с построением поверхности (в 2-мерии линии) которая отделяет различные классы. Нас будет интересовать выбор оптимальной архитектуры, которая позволяет решать данную задачу.
Выпуклые области
Пусть объекты, помеченные крестиками, в пространстве признаков занимают треугольную область, подобно примеру на рисунке ниже:

Такие объекты можно легко распознать при помощи сети [2,3,1] с одним скрытым слоем, содержащем три нейрона. Выше векторы нормалей разделяющих плоскостей нейронов направлены внутрь треугольника. Поэтому все крестки в пространстве выходов скрытого слоя y1,y2,y3 собираются в окрестности угла единичного куба с координатами (1,1,1). Соответственно, эту область несложно отсечь единственной разделяющей 3-мерной плоскостью, роль которой выполняет выходной нейрон, реализующий логическое "И". Если через A обозначить утверждение "точка лежит по вектору нормали к плоскости нейрона A" и аналогично для B и С, то приведенная выше нейронная сеть вычисляет логическую функцию A & B & C.
Так как граница области изломана, три нейрона входного слоя достаточно уверены в себе (длины векторов велики). Выходной нейрон имеет малое среднее значение выхода (0.11), что связано с преобладанием объектов класса 0 (синие кружочки). Вообще говоря, при обучении желательно иметь примерное одинаковое число объектов различных классов. Это позволяет лучше контролировать полезность нейронов. Выше на полезность выходного нейрона указывает его относительно большая волатильность 0.31.
Сети с небольшим числом нейронов способны также описывать гладкие поверхности, разделяющие классы. Ниже объекты, помеченные крестиками находятся внутри круга радиуса 0.25. Сеть [2,3,1] с такой же архитектурой, как у треугольника, генерит на выходе достаточно аккуратный круг:

Обратим внимание, что нейроны скрытого слоя в 10 раз менее уверены в себе, чем в случае с треугольником. В результате этого их границы более размыты, что приводит к сглаживанию углов треугольника. А вот выходной нейрон очень в себе уверен, что даёт чёткую границу между синей и красной областями.
4. Если в пространстве признаков существует единственная область с выпуклой границей, содержащая объекты данного класса, то они могут быть распознаны при помощи сети с одним скрытым слоем.
В качестве полезного упражнения стоит поиграться с параметрами нейронов сети с архитектурой [2,H,1], где число нейронов H скрытого слоя можно изменять. Плоскости нейронов всё время фиксированы вдоль сторон правильного H-угольника радиуса R=0.4 (его также можно изменять). Первый параметр wH определяет длину векторов нормали нейронов скрытого слоя. Следующий параметр w - это длина нормали выходного нейрона, а w0 - его сдвиг (в процентах от длины диагонали квадрата). Меняя эти 4 параметра необходимо перейти от правильного H-угольник к окружности.
| Cкрытый слой: | wH - длина нормали; R - радиус многоугольниа (w0); |
| Выходной нейрон: | w - длина нормали; shift - % пересечения диагонали; |
| H: |
|---|
| wH: | 100 | |
|---|---|---|
| R: | 0.4 | |
| w: | 40 | |
| shift: | 1.0 |
| 3: | 38, | -87, | 50| | 100| | y:0.50(0.00) |
| 4: | 70, | -0, | -100| | 100| | y:0.50(0.00) |
| 5: | -48, | 87, | 50| | 100| | y:0.50(0.00) |
| 6: | -69, | 23, | 23, | 23| | 40| | y:0.50(0.00) |
| 6: | w0/|w|:-1.73, | cos:1.00, | shift:1.00 |
[Подсказки: (3:200,0.4,200,0.85); (3:7,0.55,200,0.75)]
Проблема локальных минимумов
Минимум среднеквадратичной ошибки при распознавании образов, вообще говоря, не является самоцелью. Чаще важнее минимизировать процент неправильной классификации (Miss). Однако среднеквадратичная ошибка более гладкая (дифференцируемая) функция параметров нейронов, поэтому в ряде алгоритмов оптимизации она удобнее.
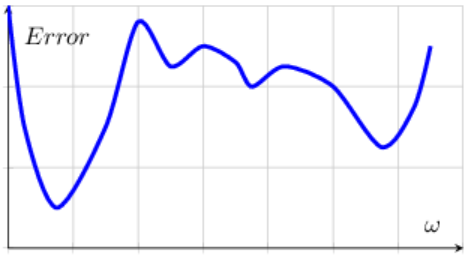 Основная проблема минимизации некоторой величины - это локальные минимумы,
в которых алгоритм может "застревать".
Справа приведен пример минимизации
функции одной переменной, имеющей один глобальный и несколько локальных минимумов.
При этом серединное "плато" с рябью мелких локальных минимумов наклонено вправо в направлении
локального минимума.
Чтобы попасть в глобальный, (самый глубокий) минимум необходимо сначала "вскарабкаться в гору".
Основная проблема минимизации некоторой величины - это локальные минимумы,
в которых алгоритм может "застревать".
Справа приведен пример минимизации
функции одной переменной, имеющей один глобальный и несколько локальных минимумов.
При этом серединное "плато" с рябью мелких локальных минимумов наклонено вправо в направлении
локального минимума.
Чтобы попасть в глобальный, (самый глубокий) минимум необходимо сначала "вскарабкаться в гору".
В многомерном случае ситуация намного сложнее, так как существует много различных путей по которым можно попасть в минимум функции. Естественно, локальные минимумы также сильно портят жизнь. Любой алгоритм поиска минимума локален. Он определяет направление движения, которое, из-за сложного рельефа (рябь на поверхности), может не иметь ни чего общего с реальным направлением к глобальному минимуму. Кроме этого, обычно, выбирается шаг (скорость обучения), с которым происходит перемещение в пространстве параметров. Если шаг велик (в он-лайн примерах это параметр Grad), то можно проскочить глобальный минимум. Если же он мал - застрять в локальном.
Вернёмся к первому примеру из предыдущего документа. Там было два класса, которые легко разделялись плоскостью. В этой задаче локальных минимумов нет и минимизация ошибки тривиальна. Это уже не так в примере с кругом, когда нейронов в скрытом слое достаточно много. Например, для сети [2,5,1], имеющей 21 параметр [5·(2+1)+1·(5+1)], глобальный минимум имеет вид:

Однако поймать такой минимум непросто. Обычно при обучении, сеть скатывается к конфигурации нейронов скрытого слоя, подобной следующему примеру:

В этой сети один нейрон (4-й) является бесполезными, что сразу видно по его среднему значению выхода. Этот локальный минимум соответствует квадрату, который можно было бы описать сетью [2,4,1].
Ещё один пример локального минимума квадрата имеет нейрон (2-й) проходящий по границе круга и приносящий мало пользы. Хотя обнаружить это по среднему и волатильности нейрона уже нельзя:
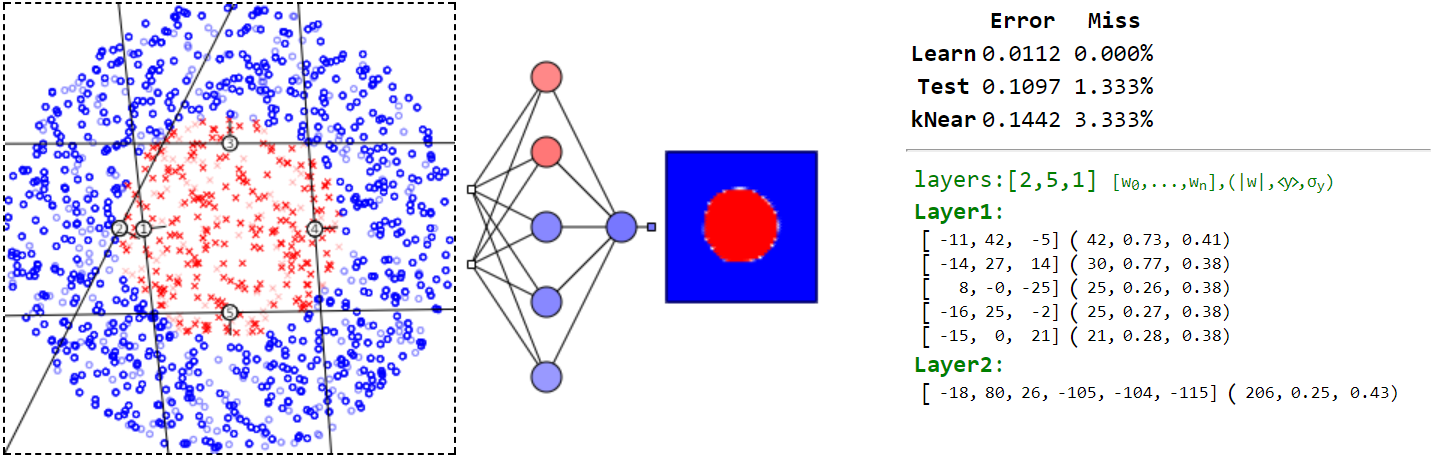
Этот локальный минимум имеет в 20 раз большую ошибку, чем когда плоскости нейронов образуют правильный пятиугольник. Кроме локальных минимумов, соответствующих треугольнику и квадрату, существуют овраги, связанные с вращением этих многоугольников, в котором параметры нейронов меняются, а ошибка - практически нет.
Ещё один интересный пример связан с квадратной границей между классами. Глобальный минимум для этой задачи выглядит следующим образом:
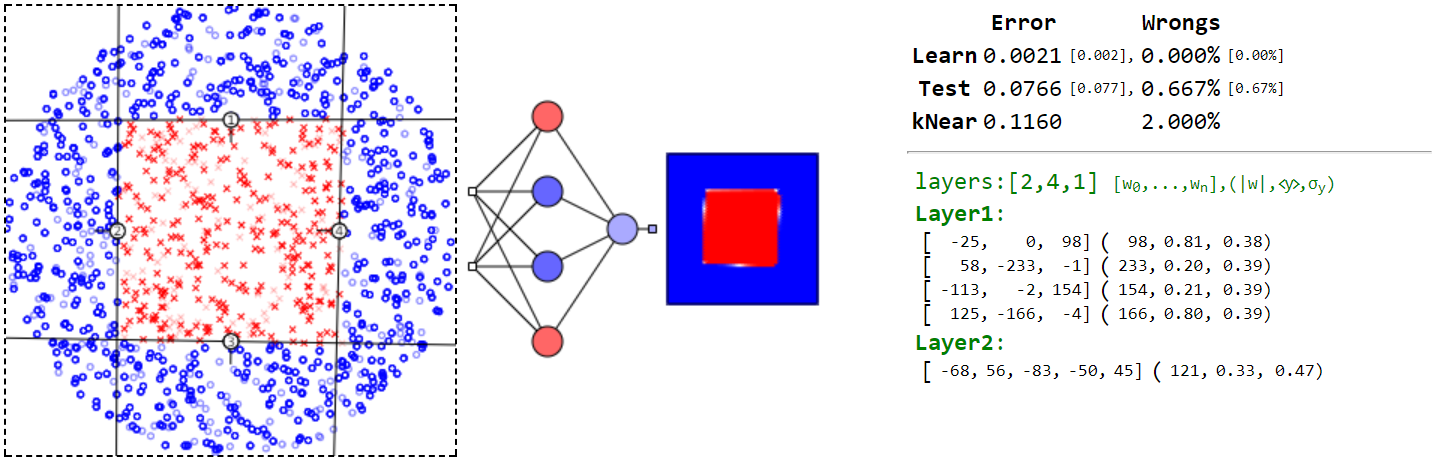
Однако, его "поймать" очень не просто и чаще алгоритм "проваливается" в следующий локальный минимум:
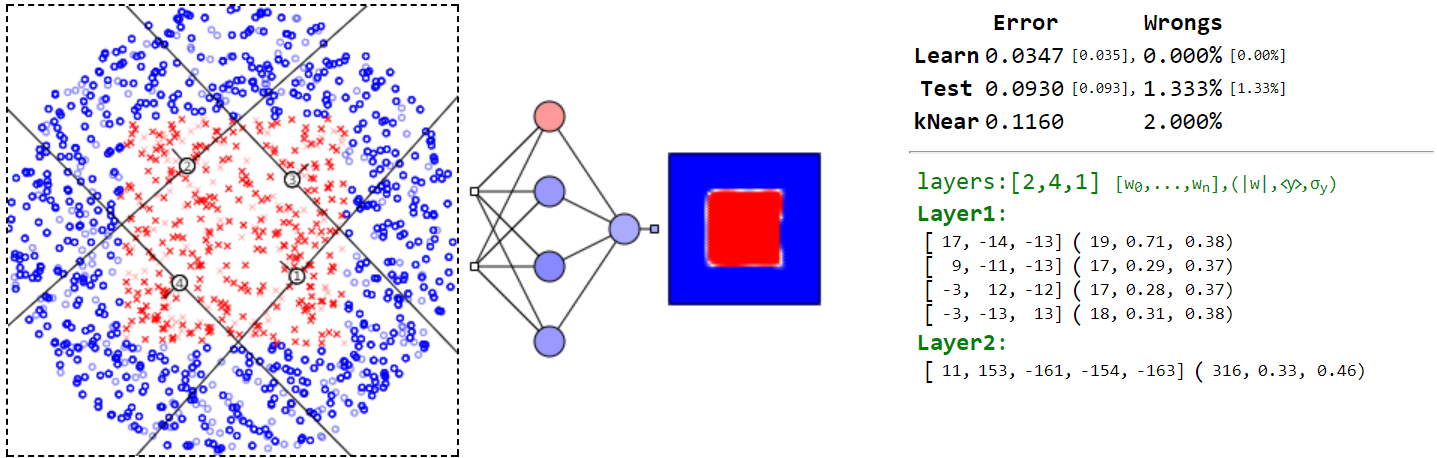
Впрочем, поиск глобального минимума не всегда является целью. Более того, достижение такого минимума может оказаться даже вредным. Рассмотрим этот вопрос чуть подробнее.
Переобученность
Чем больше нейронов и, следовательно, параметров,
тем более сложные поверхности, разделяющие классы можно описать при помощи нейронной сети.
Однако тут возникает проблема. Иногда, после обучения, ошибка по обучающим данным оказывается
малой, а по тестовым, наоборот, большой.
В этом случае говорят, что наступила переобученность системы.
 Обычно такое происходит в сильно зашумлённых данных.
Классический пример в одномерном случае - это аппроксимация данных некоторой функцией
y=f(x).
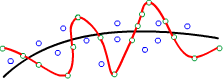
Справа на картинке красная, волнистая кривая построена по зелёным точкам, которые были выбраны в качестве
обучающих. Эта кривая максимально "старательно" проходит через все обучающие объекты и имеет
на них нулевую ошибку. Однако на тестовых объектах (синие точки) лучше сработает
более гладкая, чёрная линия. Поэтому уменьшение числа нейронов и связей между ними необходимо не только чтобы
уменьшить число параметров которые необходимо подбирать.
Если без сильного увеличения ошибки, можно уменьшить число нейронов и связей между ними,
это необходимо делать.
Такая сеть приводит к более гладкой разделящей поверхности
и меньшей вероятности возникновения эффекта переобученности.
Обычно такое происходит в сильно зашумлённых данных.
Классический пример в одномерном случае - это аппроксимация данных некоторой функцией
y=f(x).
Справа на картинке красная, волнистая кривая построена по зелёным точкам, которые были выбраны в качестве
обучающих. Эта кривая максимально "старательно" проходит через все обучающие объекты и имеет
на них нулевую ошибку. Однако на тестовых объектах (синие точки) лучше сработает
более гладкая, чёрная линия. Поэтому уменьшение числа нейронов и связей между ними необходимо не только чтобы
уменьшить число параметров которые необходимо подбирать.
Если без сильного увеличения ошибки, можно уменьшить число нейронов и связей между ними,
это необходимо делать.
Такая сеть приводит к более гладкой разделящей поверхности
и меньшей вероятности возникновения эффекта переобученности.
Вернёмся к модельному примеру с кругом. Когда он аппроксимировался треугольником (сеть [2,3,1]) ошибка равнялась Error=0.0472. Для пятиугольника она существенно меньше: Error=0.0047. Однако в обоих случаях ошибка по тестовым примерам была примерно одинакова (Error~0.1) и заметно больше, чем при обучении.
Общая рекомендация может быть такая. Часть обучающего множества объектов выделяются в отдельную, контрольную группу. Эти объекты не участвуют в подстройке параметров нейронов и контролируют, имеет ли смысл использовать более сложную архитектуру сети.
Когда необходимы два скрытых слоя
Рассмотрим разделяющие поверхности для иногда которых не достаточно одного скрытого слоя. Пусть один из классов занимает в пространстве область с вмятинами (т.е. разделяющая поверхность не выпуклая) подобно конверту с красными крестиками на рисунке ниже:
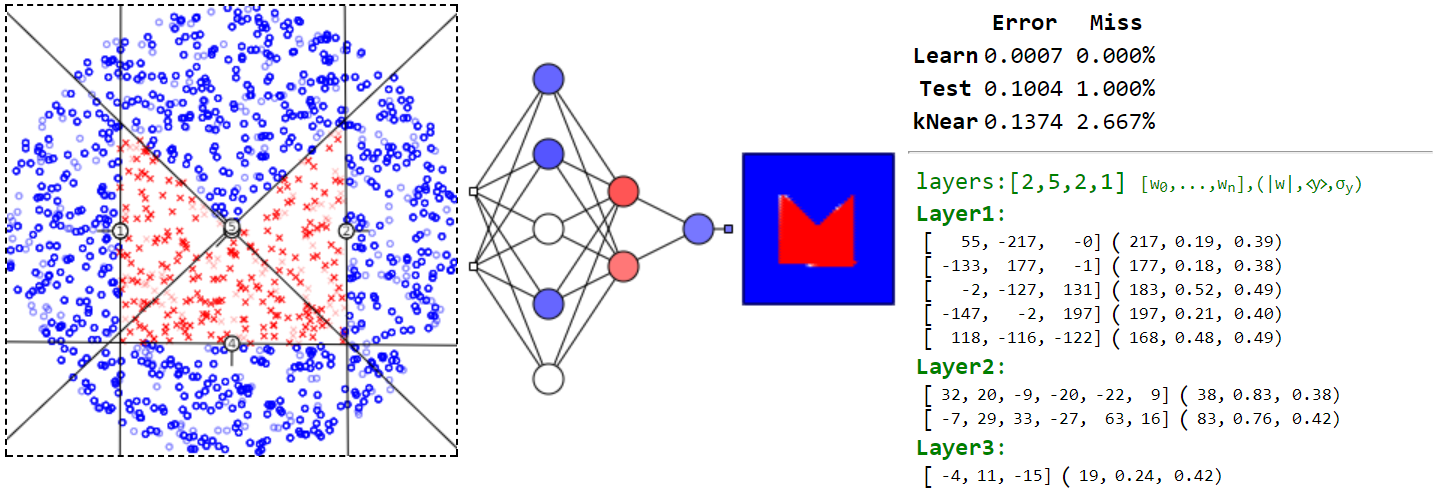
Чтобы очертить границы этого конверта необходимо 5 плоскостей-нейронов первого скрытого слоя. Но при помощи только логического "И" описать условие попадания крестика внутрь конверта нельзя.
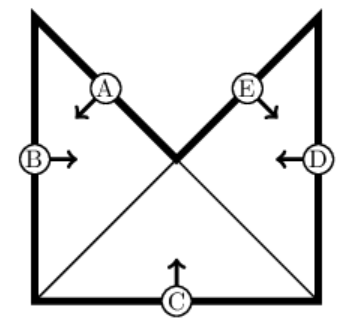 Любую плоскую фигуру можно рабить на треугольники. В примере выше таких треугольников два.
Чтобы проверить попадание объекта внутрь треугольника, необходимо три нейрона.
Справа на рисунке это линии A,B,C и С,D,E.
Объект может находиться в любом из этих треугольников или в обоих сразу в области их пересечения.
Поэтому логическое условие требует дополнительного логического "ИЛИ", которое мы обозначаем символом "∨":
Любую плоскую фигуру можно рабить на треугольники. В примере выше таких треугольников два.
Чтобы проверить попадание объекта внутрь треугольника, необходимо три нейрона.
Справа на рисунке это линии A,B,C и С,D,E.
Объект может находиться в любом из этих треугольников или в обоих сразу в области их пересечения.
Поэтому логическое условие требует дополнительного логического "ИЛИ", которое мы обозначаем символом "∨":
Оно означает: "или в треугольнике A,B,C или в треугольнике С,D,E или в обоих". Ниже на рисунке представлена оптимальная архитектура сети для этой задачи. Нейроны первого скрытого слоя являются плоскостями (прямыми), образующими стороны треугольников A,B,C и С,D,E. Два нейрона F и G следующего слоя реализуют логические "И" (точка попала в треугольник A,B,C, точка попала в треугольник С,D,E). Наконец, выходной нейрон обеспечивает логическое "ИЛИ":
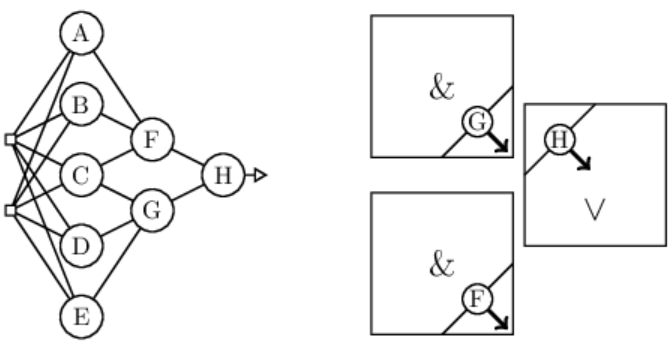
В квадратах приведено положение плоскостей нейронов во втором и третьем скрытых слоях. При этом первые два квадрата, на самом деле необходимо нарисовать как кубы (у нейронов три входа). В этих кубах нейроны G и F отсекают угол с координатами (1,1,1) и в этот же угол направляют вектора своих нормалей.
Несвязные области
Приведём ещё пример "Пуговица", в котором объекты, помеченные красными крестиками, находятся внутри двух несвязных кругов. При этом они окружены объектами другого класса:
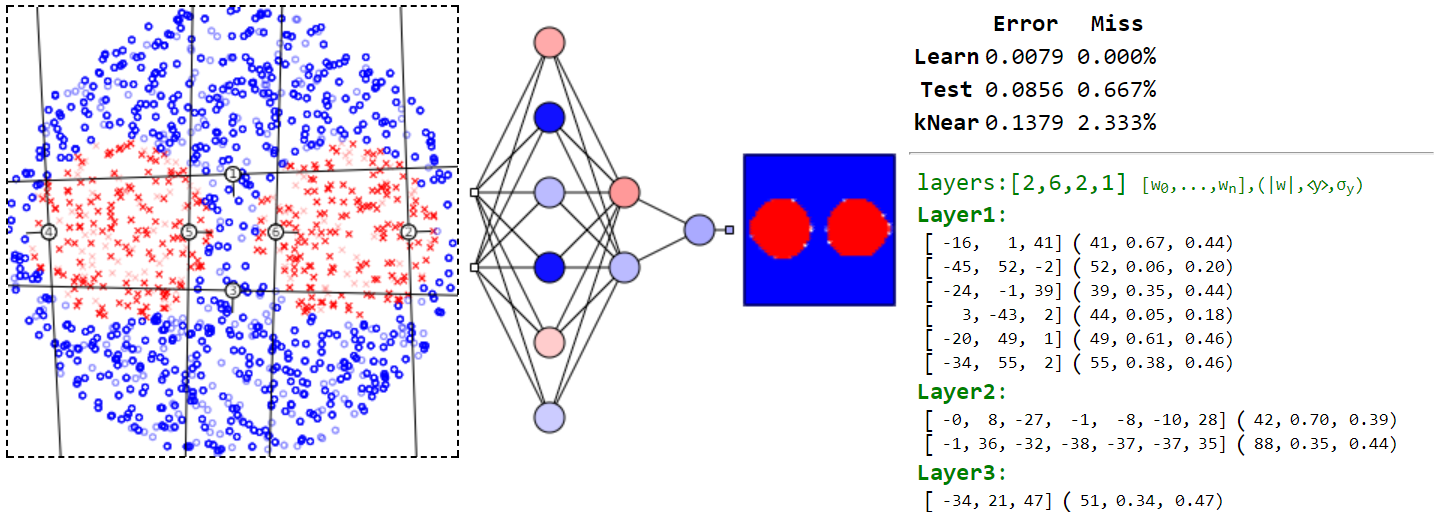
5. Любую поверхность в пространстве признаков (в т.ч. несвязную и вогнутую) всегда можно описать сетью с двумя скрытыми слоями.
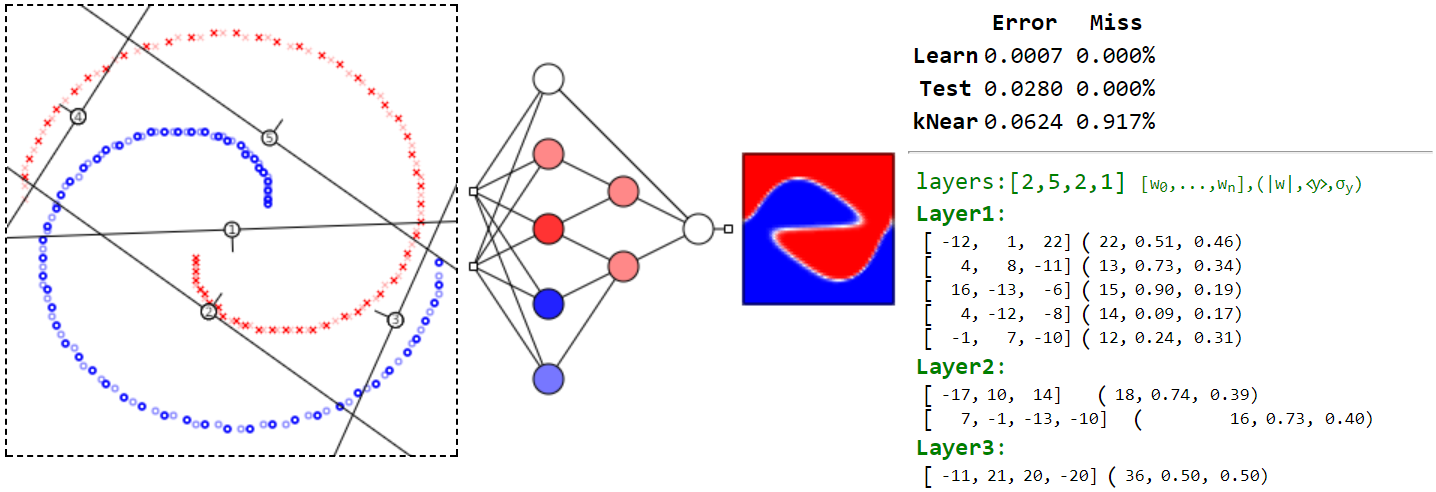
Предлагается самостоятельно проанализировать два класса, объекты которых расположены на двух спиралях. Записав соответствующее логическое выражение, необходимо показать что "минимально-оптимальная" архитектура нейронной сети, описывающая разделяющую поверхность должна быть такой как на рисунке ниже.
Иногда достаточно и одного слоя
 Любопытно, что в приведенных выше примерах, на самом деле, достаточна нейронная сеть с одним скрытым слоем.
Для конверта две вертикальные линии
и одна горизонтальная более значимы, так как против векторов их нормалей нет ни одного
крестика. Поэтому присвоим их выходам веса 2.
Наклонные прямые менее значимы, так как крестики могут находиться с любой их стороны.
Их выходам присвоим вес 1.
Любопытно, что в приведенных выше примерах, на самом деле, достаточна нейронная сеть с одним скрытым слоем.
Для конверта две вертикальные линии
и одна горизонтальная более значимы, так как против векторов их нормалей нет ни одного
крестика. Поэтому присвоим их выходам веса 2.
Наклонные прямые менее значимы, так как крестики могут находиться с любой их стороны.
Их выходам присвоим вес 1.
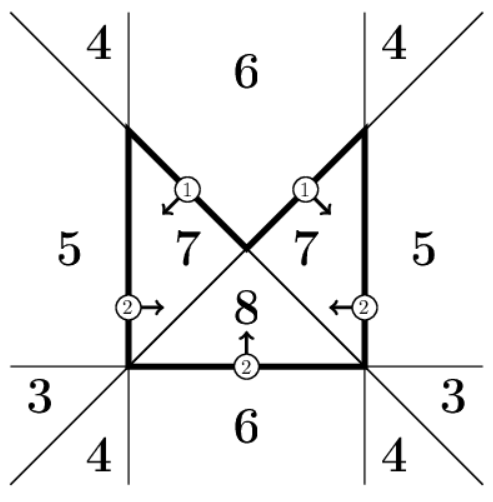
Пусть yA,...,yE - выходы скрытого слоя.
Вычислим сумму:
где yA, yE - выходы нейронов наклонных линий. Значения d для различных областей приведены справа на рисунке. Вне конверта находятся значения 3,4,5,6, а внутри конверта: 7,8. Понятно, что эти два класса легко разделить одним нейроном:
где множитель 100 выбран для повышения уверенности выходного нейрона (сигмоидная функция - ступенька).
Аналогичным образом предлагается проанализировать пример "Пуговица", в котором менее значимыми для выделения крестиков являются две внутреннии вертикальные линии.
6. Чем больше вес входа нейрона, тем более значим этот вход.
Бесполезные бывают полезными
Рассмотрим 3 класса и сеть без скрытых слоёв. Она выдаёт большую ошибку на втором выходе (нейрон 4), но правильно классифицирует все объекты. Как её это удаётся?
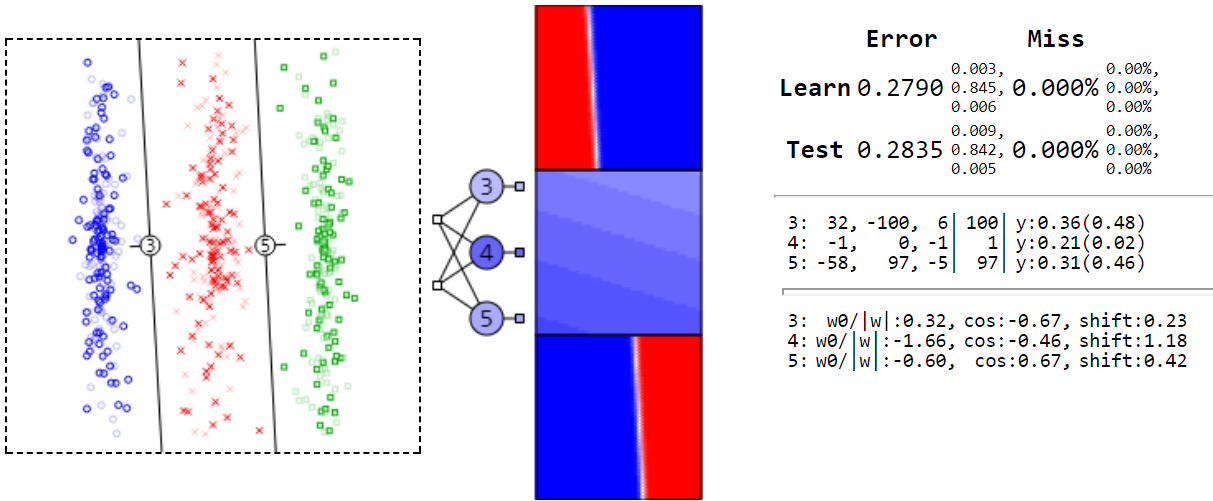
Нейроны 3,5 смотрят в сторону своих классов (синие круги, зелёные квадраты) и очень уверены в себе. Поэтому на их выходах будет 1 для своего класса и 0 - для остальных. Нейрон 4 практически всегда на выходе имеет y=0.21. Поэтому он даст максимальный голос для красных крестиков (т.к. остальные там равны нулю).