Многомерные пространства

Введение

Мы живём в 3-мерном пространстве. Оно для нас на столько привычно, что свойства пространств большого числа измерений часто оказываются неожиданными. Тем не менее, именно с такими пространствами имеют дело при распознавании образов (классификации объектов). Напомним, что мы рассматриваем объекты которые характеризуются n вещественными числами. После соответствующей нормировки их можно считать принадлежащими интервалу от 0 до 1. Таким образом, каждый объект представим точкой, находящейся внутри n-мерного единичного гиперкуба. Рассмотрим некоторые математические аспекты многомерия.

Гиперкуб

Единичный 2-мерный куб (квадрат) имеет 4 вершины с координатами (0,0), (0,1), (1,0), (1,1). У 3-мерного куба их уже 8.

В пространстве n измерений каждая точка характеризуется n координатами: {x1,...,xn}. Пусть одна вершина куба находится в начале координат: {0,0,...,0} (n нулей). Тогда остальные вершины нумеруются всеми возможными последовательностями n нулей и единиц: {0,0,...,0}, {1,0,...,0}, ..., {1,1,...,1}. Существует 2n двоичных чисел с n разрядами, поэтому:

Гиперкуб в n измерениях имеет 2n вершин

При больших n гирперкуб очень "колючий" объект. Например, в пространстве с 32 признаками он имеет 4294967296 вершин.

Из каждой из $2^n$ вершин гиперкуба выходит $n$ рёбер (для вершины (0,0,...,0) это координатные оси). Поэтому всего у гиперкуба $n\,2^n/2=n\,2^{n-1}$ рёбер.

Гиперкуб имеет $2\,n$ "сторон" являющихся $(n-1)$-мерными кубами (у 3-куба 6 сторон-квадратов). Кроме этого, гиперкуб можно получить соединением рёбрами вершин двух $(n-1)$-мерных кубов (для "обычного" куба это два квадрата). При этом:

число вершин: $2^{n-1}+2^{n-1}=2^n$, число рёбер: $(n-1)\,2^{n-2}+(n-1)\,2^{n-2}+2^{n-1}=n\,2^{n-1}$.

Гипотеза компактности

Предположим, что мы хотим равномерно заполнить гиперкуб точками (обучающими объектами). Для этого каждый признак (ось) разобьём на k равных частей. В результате получится kn кубиков, в каждый из которых можно поместить точку. Понятно, что даже при k = 2 и n = 32 это сделать практически невозможно. Таким образом, многомерное пространство очень большое.

Необходимо стремится к такому отбору признаков объектов, при котором соответствующие их классам образы не были бы слишком сложными. Иногда это формулируют в виде гипотезы компактности:

Каждый класс должен занимать относительно компактную область в n-мерном пространстве и различные классы могут быть отделены друг от друга сравнительно простыми поверхностями.
В противном случае задача не только распознавания, но и даже подготовки обучающего множества становится очень нетривиальной задачей.

Шар

Множество равноудалённых точек от данной (центра) называется сферой. Пространство внутри сферы называется шаром. Шар, вписанный в гиперкуб это очень "маленький" объект. Объёма шара радиуса $R$ в пространствах равен: $$ {\displaystyle V_{n}(R)={\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}}+1)}}\,R^{n}},~~~~~~~~~~~~~~~~~~V_{2k}(R) = \frac{\pi^k}{k!}\,R^{2k}, $$ где $\Gamma(x)$ - гамма-функция (вторая формула приведена для чётного числа измерений). Напомним, что:

◄ Интегральное определение гамма функции (второй интеграл - замена $t=x^2$): $$ \Gamma(z) = \int\limits^\infty_{0} t^{z-1}\, e^{-t}\, dt = 2\int\limits^\infty_0 x^{2z-1}\, e^{-x^2}\, dx. $$ Интегрированием по частям и интегрированием в частных случаях $z=1,2$, несложно получить свойства гамма-функции: $$ \Gamma(z+1) = z\, \Gamma(z),~~~~~~~~~~~~\Gamma(1) = 1,~~~~~~~~~~~\Gamma(1/2) = \sqrt{\pi}. $$ ►

Докажем теперь формулу для объёма $n$-мерного шара:

◄ В 2-мерном случае (плоскость) элемент объёма (площади) в полярных координатах равен $d^2x=rdr\,d\phi = rdr\,d\Omega$.
Поэтому объём 2-мерной сферы радиуса $R$ (площадь круга) равен $V_2=\pi R^2$, а полный телесный угол $\Omega_2=2\pi$.
Аналогично для трёхмерного пространства $d^3x = r^2 dr\,d\Omega$, поэтому $V_3=(4/3)\pi R^3$ и $\Omega_3=4\pi$.
Для $n$-мерного случая вычислим произведение $n$ гауссовых интегралов ($r^2=x^2_1+...+x^2_n$): $$ \int\limits^\infty_{-\infty} e^{-(x^2_1+...+x^2_n)}\, d^n x = \int\limits^\infty_{0} e^{-r^2}\, r^{n-1}\,d r \int d\Omega = \frac{1}{2}\,\Gamma(n/2) \int d\Omega = \pi^{n/2}, $$ где последнее равенство получено возведением в $n$-ю степень (первый интеграл) гауссова интеграла. Теперь несложно записать $n$-мерный телесный угол и объём $n$-мерной сферы радиуса $R$: $$ \Omega_n = \int d\Omega= \frac{2\,\pi^{n/2}}{\Gamma(n/2)},~~~~~~~~~~~~~V_n = \frac{\Omega_n R^n}{n}. $$ ►

В единичный гиперкуб можно вписать шар радиуса R=1/2. Его объём при n=10 равен V10=0.0025, а при n=32 он исчезающе мал: V32=10-15. Хотя шар "прижимается" к граням гриперкуба, его окружает очень много (2n) углов.

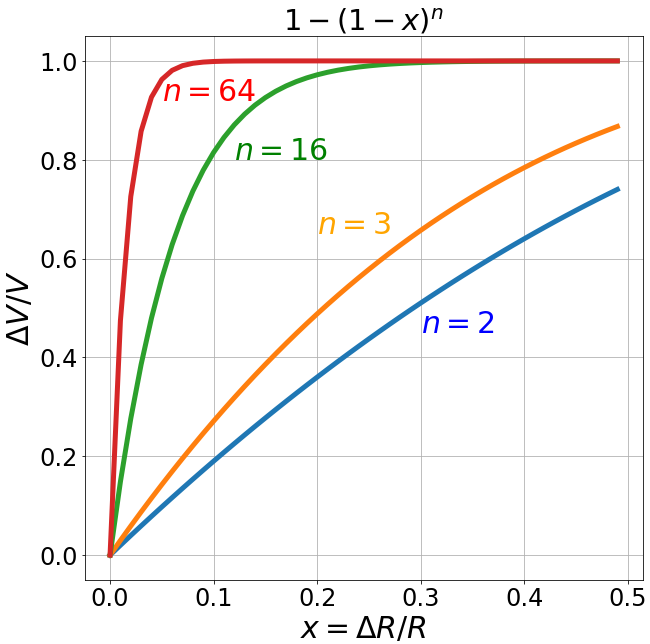Ещё одна особенность n-мерного шара состоит в том, что почти весь его объём сосредоточен возле поверхности. Действительно, рассмотрим два вложенных друг в друга шара. Один радиуса R, второй - радиуса R-ΔR. Разность их объёмов равна объёму сферического слоя между ними. Отношение его объёма к объёму шара радиуса R приведено на рисунке справа для различных размерностей пространства n.

Пусть шар равномерно (с постоянной плотностью) заполнен объектами. Случайно выбранный объект (при больших $n$) почти наверняка окажется возле поверхности шара.

Пусть объекты данного класса характеризуются некоторыми типичными (средними) значениями признаков с небольшим разбросом вокруг этих средних значений. Тогда образ этого класса является центром шара в n-мерном пространстве. Чем меньше разброс вокруг среднего, тем меньше радиус такого шара-образа. Если у разных признаков разброс имеет различную амплитуду, то шар превращается в эллипсоид. Линейным преобразованием всегда можно превратить эллипсоид в шар. Однако, если в пространстве признаков существует несколько различных эллипсоидов, то линейным преобразованием превратить в шар можно только один из них.

m-мерные плоскости

Пусть $\mathbf{x}=\{x^1,...,x^n\}$ - точка в $n$-мерном пространстве (верхний индекс - номер координаты). Поверхность размерности $m$ можно описать параметрическим образом $$ \mathbf{x} = \mathbf{f}(t_1,...,t_m), $$ где $t_k$ - набор скалярных параметров (их количество равно размерности поверхности). Например, единичная сфера в 3-мерном пространстве описывается двумя (2-мерный объект) углами $\{t_1,t_2\}=\{\theta,\phi\}$: $$ x = \sin \theta \cos\phi, ~~~~~y = \sin \theta \sin\phi,~~~~~z = \cos \theta. $$ Самой простой $m$-мерной поверхностью является плоскость. Пусть $\mathbf{e}_k=\{\mathbf{e}_1,...,\mathbf{e}_m\}$ - набор $m$ единичных, попарно ортогональных векторов ($\mathbf{e}_k\mathbf{e}_p=\delta_{pk}$, где $\delta_{pk}$ - символ Кронекера). Тогда уравнение плоскости имеет вид: \begin{equation}\label{plane_eq} \mathbf{x}= \mathbf{x}_0 + \sum^m_{k=1} t_k\mathbf{e}_k. \end{equation} Параметры $\{t_1,...,t_m\}$ выступают декартовыми координатами в $m$-мерном пространстве с базисом $\{\mathbf{e}_1,...,\mathbf{e}_m\}$. Вектор $\mathbf{x}_0$ задаёт положение начала координат (точка в которой все координаты $t_k$ на плоскости равны нулю). Уравнение (\ref{plane_eq}) является первым приближением разложения в ряд Тейлора произвольной поверхности $\mathbf{x} = \mathbf{f}(t_1,...,t_m)$ в окрестности точки $t_1=...=t_m=0$. Если $m=1$, то (\ref{plane_eq}) будет уравнением прямой (одномерный объект). При $m=2$ мы имеем двумерную плоскость и т.д.

Расстояние до $m$-плоскости

Получим выражение для кратчайшего евклидового расстояния $(\mathbf{x}-\mathbf{X})^2$ от произвольной точки $\mathbf{X}$ до $m$-плоскости (\ref{plane_eq}). Для этого необходимо найти параметры $t_k$ для которых это расстояние минимально: $$ d^2 = \bigr(\mathbf{x}_0-\mathbf{X} + \sum^m_{k=1} t_k\mathbf{e}_k\bigr)^2 = min. $$ Возьмём производную по $t_p$, приравняем её нулю и учтём ортонормированность векторов $\mathbf{e}_k$: $$ \bigr(\mathbf{x}_0-\mathbf{X} + \sum^m_{k=1} t_k\mathbf{e}_k\bigr)\,\mathbf{e}_p = (\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_p + t_p = 0 ~~~~~~~~\Rightarrow~~~~~~~t_p = -(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_p. $$ Подставим эти $t_p$ в квадрат расстояния $d^2$: $$ d^2 = \bigr(\mathbf{x}_0-\mathbf{X} - \sum^m_{k=1} \bigr[(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_k \bigr]\,\mathbf{e}_k\bigr)^2. $$ Возводя в квадрат (снова с учётом ортогональности), это выражение можно переписать в следующем виде: \begin{equation}\label{d2_to_plane} d^2 = \bigr(\mathbf{x}_0-\mathbf{X}\bigr)^2 - \sum^m_{k=1} \bigr[(\mathbf{x}_0-\mathbf{X})\,\mathbf{e}_k \bigr]^2. \end{equation} Проекция точки $\mathbf{X}$ на плоскость получается подстановкой найденных параметров $t_k$ в уравнение плоскости (\ref{plane_eq}): \begin{equation}\label{projec_coord} \mathbf{X} ~\mapsto~\mathbf{x}=\mathbf{x}_0 + \sum^m_{k=1} \bigr[(\mathbf{X}-\mathbf{x}_0)\,\mathbf{e}_k\bigr]\mathbf{e}_k. \end{equation}

Гиперплоскость

Гиперплоскостью в $n$-мерном пространстве называют $(n-1)$-мерное пространство (в 2-мерии это линия, а в 3-мерии "обычная" плоскость). Таким образом, гиперплоскость это $(n-1)$-плоскость ($m=n-1$). Гиперплоскость всегда можно провести через $n$ точек. Соответственно, она задаётся при помощи $n$ чисел (например, единичным ($\boldsymbol{\omega}^2=1$) вектором нормали (перпендикуляра) к плоскости $\boldsymbol{\omega} = \{\omega^1,....,\omega^n\}$ и параметром сдвига $\omega_0$.

Пусть гиперплоскость проходит через точку $\mathbf{x}_0$ и имеет вектор нормали $\boldsymbol{\omega}$. Тогда расстояние d от гиперплоскости до некоторой точки $\mathbf{X}=\{X^1,...,X^n\}$ вычисляется по формуле

$$ d = \omega_0 + \boldsymbol{\omega}\mathbf{X},~~~~~~~~~~~~\omega_0 = -\boldsymbol{\omega}\mathbf{x}_0. $$

При этом $d > 0$, если точка $\mathbf{X}$ лежит с той стороны плоскости, куда указывает вектор $\boldsymbol{\omega}$ и $d < 0$, если с противоположной. Когда $d=0$ - точка $\mathbf{X}$ лежит в плоскости. Изменение параметра $\omega_0$ сдвигает плоскость параллельным образом в пространстве. Если $\omega_0$ уменьшается, то плоскость смещается в направлении вектора $\boldsymbol{\omega}$ (расстояние меньше), а если $\omega_0$ увеличивается - плоскость смещается против вектора $\boldsymbol{\omega}$. Это непосредственно следует из приведенной выше формулы.

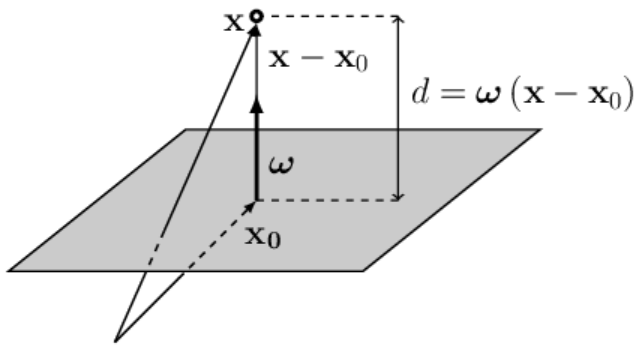◄ Запишем вектор $\mathbf{X}-\mathbf{x}_0$, начинающийся в точке $\mathbf{x}_0$ (лежащей в плоскости) и направленный в точку $\mathbf{X}$ (векторы складываются по правилу треугольника). Точка $\mathbf{x}_0$ выбрана в основании вектора $\boldsymbol{\omega}$, поэтому $\boldsymbol{\omega}$ и $\mathbf{X}-\mathbf{x}_0$ коллинеарны (лежат на одной прямой). Если вектор $\boldsymbol{\omega}$ единичный ($\boldsymbol{\omega}^2=1$), то скалярное произведение векторов $d=\boldsymbol{\omega}\,(\mathbf{X}-\mathbf{x}_0)$ равно расстоянию $d$ точки $\mathbf{X}$ до плоскости.

Если длина $\omega=|\boldsymbol{\omega}|$ вектора $\boldsymbol{\omega}$ отлична от единицы, то $d$ в $\omega$ раз больше ($\omega > 1$) или меньше ($\omega < 1$) евклидового расстояния в $n$-мерном пространстве. Когда векторы $\boldsymbol{\omega}$ и $\mathbf{X}-\mathbf{x}_0$ направлены в противоположные стороны: $d < 0$. ►

Если пространство имеет n измерений, то гиперплоскость это (n-1)-мерный объект.
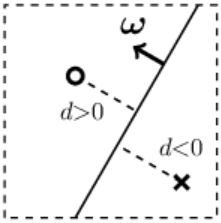
Она делит всё пространство на две части. Для наглядности рассмотрим 2-мерное пространство. Гиперплоскостью в нём будет прямая линия (одномерный объект). Справа на рисунке кружок изображает одну точку пространства, а крестик - другую. Они расположены по разные стороны от линии (гиперплоскости). Если длина вектора ω много больше единицы, то и расстояния d от точек к плоскости по модулю будут существенно большими единицы.

Уравнение гиперплоскости, аналогично $m$-плоскости, можно записать в параметрическом виде при помощи $n-1$ векторов базиса $\{\mathbf{e}_1,...,\mathbf{e}_{n-1}\}$. Все эти векторы ортогональны вектору нормали: $\boldsymbol{\omega}\mathbf{e}_k=0$.

Симплекс

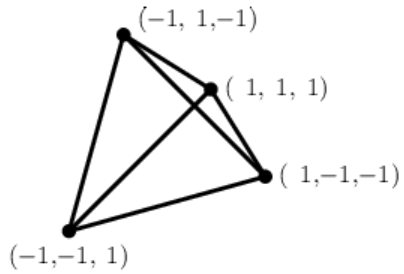Симплексом называют n мерное обобщение треугольника 2-мерного пространства. В 3-мерии это тетраэдр (рисунок справа). Через n точек в n-мерном пространстве можно провести гиперплоскость. Соответственно n+1 точек в общем случае не лежат на одной гиперплоскости и образуют симплекс с n+1 вершинами. Если все рёбра (расстояния между парами вершин) одинаковы - симплекс называют правильным. Напротив каждой из n+1 вершин лежит гиперплоскость (в которую эта вершина не попала).

Каждая из $n+1$ вершин симплеса соединена со всем остальными вершинами рёбрами. Соответственно, число рёбер равно $n\,(n+1)/2$.

Объём правильного симплекса с единичными рёбрами равен: $$ V_n = \frac{\sqrt{n+1}}{n!\,2^{n/2}}. $$ Как и шар, это очень "маленький" объект.

Пусть внутри сферы находятся объекты одного класса, а вне неё - объекты другого класса. Для их разделения потребуется нейронная сеть с одним скрытым слоем, имеющая по меньшей мере n+1 нейронов в скрытом слоёв. Они образуют n+1 гиперплоскостей симплекса (возможно со сглаженными углами, если длины векторов нормали невелики).