Разделяющие поверхности

---

Введение

---

Линейные решающие правила

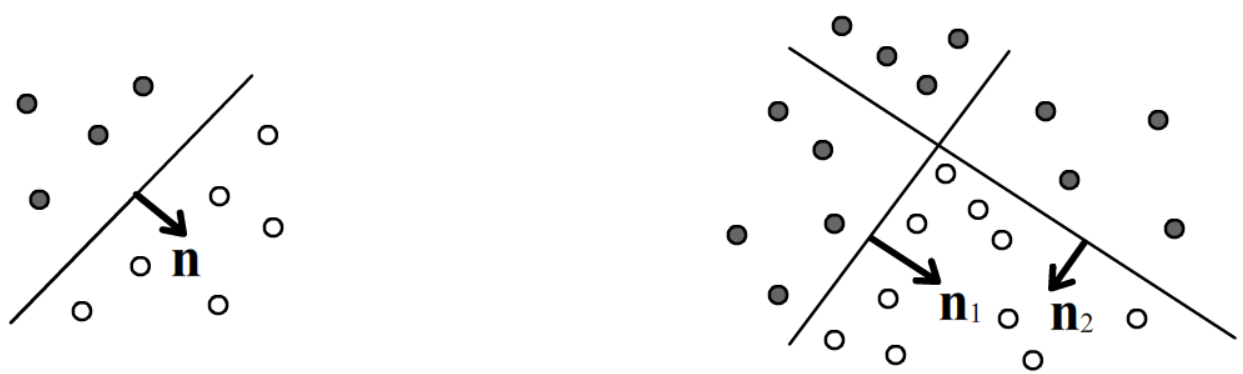
Линейные решающие правила состоят в построении гиперплоскостей в $n$-мерном пространстве, которые полностью разделяют примеры различных классов. Иногда бывает достаточно единственной плоскости, иногда их необходимо несколько:

Гиперплоскость, проходящая через точку $\mathbf{x}_0$ и имеющая единичный вектор нормали $\mathbf{n}$, описывается уравнением $(\mathbf{x}-\mathbf{x}_0)\cdot\mathbf{n}=0$ или $\mathbf{n}\mathbf{x}+n_0=0$, где $n_0=-\mathbf{n}\mathbf{x}_0.$ Если точка $\mathbf{x}$ не лежит на плоскости, то расстояние от неё до плоскости равно $$d=\mathbf{n}\mathbf{x}+n_0,$$ причём, $d \gt 0$, когда точка находится с той стороны плоскости куда направлен вектор $\mathbf{n}$, если $d \lt 0$, то с противоположной.

На рисунках выше в первом случае решающим правилом будет $d\gt 0$ для класса белых кружков и $d\lt 0$ для чёрных.
Во втором случае решающее правило для чёрного класса: ($d_1 \lt 0$ or $d_2 \lt 0$), а для белых: ($d_1 \gt 0$ and $d_2 \gt 0$), где or, and - это логические ИЛИ, И. Заметим, что на второй картинке плоскость $\mathbf{n}_1$ сначала отсекает большую часть объектов чёрного класса. После этого оставшиеся объекты двух классов уже оказываются линейно разделимыми плоскостью $\mathbf{n}_2$.

---

Дерево гиперплоскостей

Пусть в $n$-мерном пространстве есть два класса (или один и все остальные). Возьмём нейрон с $n$ входами и одним выходом $y=[0...1]$. Проведём гиперплоскость нейрона так, чтобы сумма квадратов отклонений от неё объектов различных классов (с учётом знака расстояния) была минимальна. Кроме этого будем требовать, чтобы плоскость нейрона не уходила далеко от центра масс $\mathbf{c}$ всех объектов (обоих классов): $$\mathrm{Cost} = \frac{1}{N}\,\sum^N_{i=1} \bigr(S(\mathbf{n}\mathbf{x}_i+n_0)-Y_i\bigr)^2 + \lambda\,(n_0+\mathbf{n}\mathbf{c})^2,~~~~~~~~где~~~~~ Y_i = \left\{ \begin{array}{ll} 1 & x_i\in~первый~класс, \\ 0 & x_i\in~второй~класс, \\ \end{array} \right.$$ где $S(d)=1/(1+e^{-d})$ - сигмоидная функция и $\lambda$ - величина "притяжения" нейрона к центру. В соответствии с градиентным методом, необходимо подавать различные примеры $\mathbf{x}_i$ и подправлять параметры плоскости $n_0, \mathbf{n}$ следующим образом: $$\mathbf{n}^{(t+1)}= \mathbf{n}^{(t)} - \gamma\cdot \Bigr[\bigr(y_i-Y_i\bigr)\,\mathbf{x}_i +\lambda\, d_{\mathbf{c}}\,\mathbf{c}\Bigr],~~~~~~~~~~~ n^{(t+1)}_0 = n^{(t)}_0 - \gamma\cdot \bigr[y_i-Y_i+\lambda\,d_{\mathbf{c}}\bigr],~~~~~~y_i=S(\mathbf{n}^{(t)}\mathbf{x}_i+n^{(t)}_0),~~~~~d_{\mathbf{c}}=n^{(t)}_0+ \mathbf{n}^{(t)}\mathbf{c},$$ где $\gamma$ - параметр скорости обучения и отброшен "замороженный" множитель $y\,(1-y)$.

Проведенная плоскость, разбивает обучающую выборку на две части. Алгоритм повторяется для каждой части, если в ней присутствуют объекты различных классов. В результате (при $\lambda=0$) получается древесное решающее правило:

Решающие правила для листьев дерева получаются по значению сигмоидной функции $S(d)$.

---

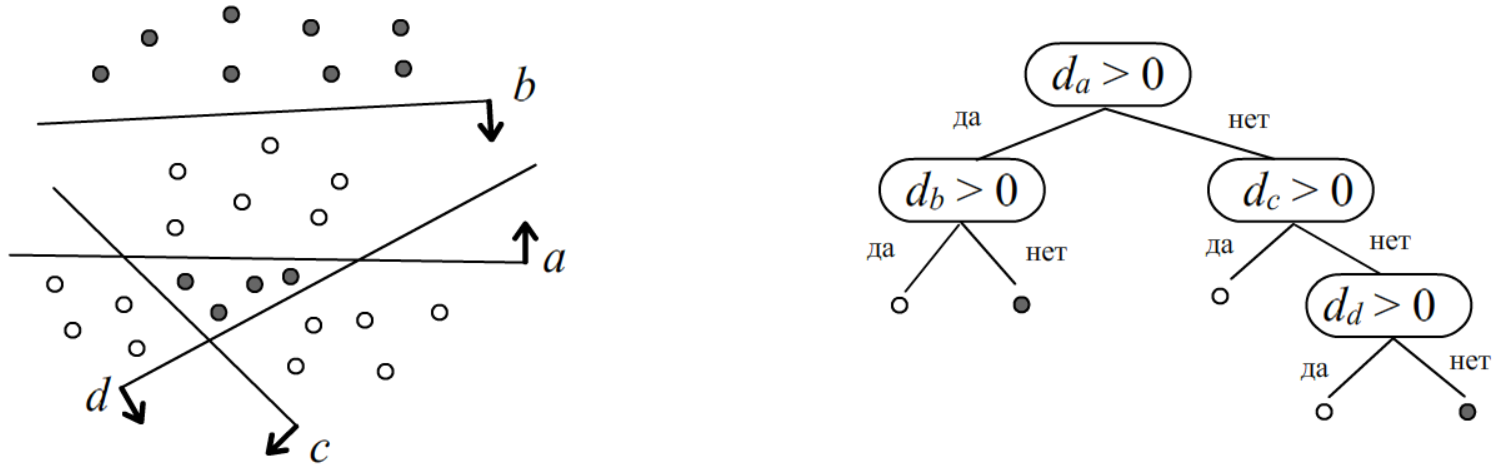
Метод опорных векторов

Если объекты двух классов линейно разделимы, между ними, вообще говоря, можно провести множество гиперплоскостей (ниже левый рисунок):

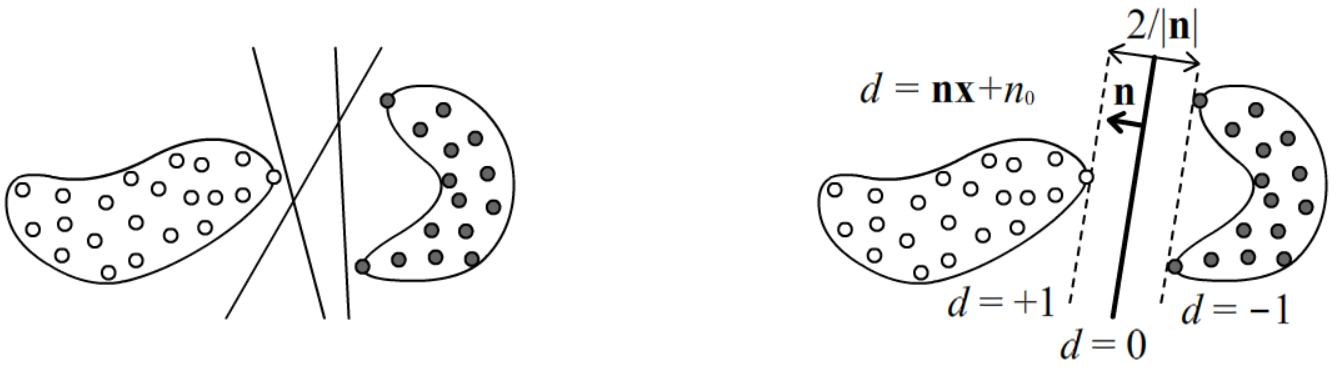
В методе опорных векторов (support vector machine, SVM) строится разделяющая классы плоскость таким образом, чтобы расстояния от неё до объектов различных классов было максимальным. Т.е. плоскость проводится так, чтобы с обоих её сторон получался максимальный зазор до примеров различных классов (выше второй рисунок).

Будем нумеровать классы $Y=\{+1,-1\}$ и минимизировать следующую сумму по всем примерам: $$\mathrm{Cost}=\sum^N_{i=1} \bigr[C_i\gt 0 \bigr],~~~~~~~~~~~C_i(\mathbf{n}, n_0) = Y_i\cdot(\mathbf{n}\mathbf{x}_i+n_0),$$ где $[истина]=1$, $[ложь]=0$, т.е. функция ошибок Cost равна числу неправильно классифицированных объектов (те, кто лежит по вектору нормали $\mathbf{n}$ имеют $\mathbf{n}\mathbf{x}_i+n_0 > 0$ и они верно классифицируются, если у них $Y_i=1$, т.е. $C_i(\mathbf{n}, n_0) > 0$; аналогично для $Y_i=-1$). Для линейно разделимых классов существуют такие $(n_0,\mathbf{n})$, что для любого $i=1,...,N$ выполняется $C_i(\mathbf{n}, n_0) > 0$. Умножением параметров плоскости $(n_0,\mathbf{n})$ на общую положительную константу можно задать следующую нормировку (Cost при этом не поменяется): $$\min_{i=1...N} C_i(\mathbf{n}, n_0) = 1.$$ В такой нормировке все объекты удовлетворяют условиям: $$-1 \le \mathbf{n}\mathbf{x}_i+n_0 \le +1.$$

Рассмотрим ближайший к плоскости пример $\mathbf{x}_+$ из класса $Y=+1$ и ближайший (с другой стороны) пример $\mathbf{x}_-$ из класса $Y=-1$. По определению нормировки: $$\left\{ \begin{array}{ll} \mathbf{n}\mathbf{x}_+ + n_0 = +1\\ \mathbf{n}\mathbf{x}_- + n_0 = -1 \end{array} \right. ~~~~~~~\Rightarrow~~~~~~~\mathbf{n}(\mathbf{x}_+-\mathbf{x}_+) = 2.$$ Учтём, что расстояние с не единичным вектором нормали равно $d=(\mathbf{n}\mathbf{x}+n_0)/|\mathbf{n}|$. Запишем суммарное расстояние до плоскости, т.е.ширину зазора $2d$: $$2d = d_+-d_- = \frac{\mathbf{n}\cdot(\mathbf{x}_+-\mathbf{x}_-)}{|\mathbf{n}|} = \frac{2}{|\mathbf{n}|}.$$ Таким образом, зазор будет максимальным, если длина нормали $|\mathbf{n}|$ минимальна при наличии ограничений (условий нормировки). В результате получается следующая оптимизационная задача: $$\frac{1}{2}\,\mathbf{n}^2 = \min,~~~~~~~~при~~N~~ограничениях:~~~~C_i(\mathbf{n}, n_0) \ge 1,~~~i=1,...,N.$$

Метод опорных векторов легко обощается на случай линейно неразделимых классов, а также на нелинейные гиперповерхности, которые называются ядрами.

---

Полезная информация

• [1] Воронцов К.В. ""
• Отрывок из семинара

---