Методы эталонов и ближайших соседей

---

---

Введение

Этот документ и 4 следующих содержат обзор классических методов классификации (распознавания образов). Несмотря на их простоту, при удачном выборе признаков объектов, классические методы приводят к хорошим результатам. А их комбинация, при помощи технологии бустинга (см. ниже), может оказаться очень эффективной. Условно методы можно разделить на следующие группы:

• Методы эталонов - объекты каждого класса занимают достаточно компактную область в пространстве признаков. Можно выделить эталонное описание класса.


• Методы ближайших соседей (lazy learning) - почти не учатся, а просто помнят все обучающие примеры. Хотя иногда и учатся, становясь эталонными.


• Разделяющие поверхности - между объектами, которые отделяют одни классы от других. Компактности классов при этом не требуется, только их отделимость.


• Вероятностные методы - учитывают количественный состав обучающих примеров различных классов и плотности вероятностей распределения их в пространстве.


• Деревья принятия решений - могут эффективно учитывать скачкообразный характер принадлежности к классу при изменении признаков.


• Композиция методов (бустинг) - улучшение качества распознавания в результате объединения различных методов.

Некоторые из методов будут более подробно описаны в отдельных документах.

---

Метод эталонов

Центр масс всех объектов данного класса иногда неплохо характеризует типичный "образ" класса. Образ (точка в пространстве признаков) может не совпадать ни с одним из обучающих примеров.

Для получения подобного эталонного представителя класса вычисляется простое среднее по всем обучающим примерам $i=1,..,N_k$ данного класса $k$: $$\mathbf{c}_k = \frac{1}{N_k} \sum^{N_k}_{i=1} \mathbf{x}_i,~~~~~для~~~\mathbf{x}_i~\in~классу~k.$$ Процесс классификации сводится к поиску эталона который находится ближе всего к тестовой точке: $$\begin{equation}\label{etal_dist} d(\mathbf{x}, \mathbf{c}_k)= \mathrm{min}~~~~~~\Rightarrow~~~~~~~\mathbf{x}~~\in~классу~k,~~~~~~~~~~~~~~или~~~~~~~~~~~~~k=\arg\min_k d(\mathbf{x}, \mathbf{c}_k). \end{equation}$$ В качестве $d(\mathbf{x}, \mathbf{c}_k)$ можно взять любое метрическое расстояние, например, евклидово: $d(\mathbf{x}, \mathbf{c}_k)=|\mathbf{x}- \mathbf{c}_k|=\sqrt{(\mathbf{x}- \mathbf{c}_k)^2}$.

Сферы эталонов обычно имеют различный размер. Радиус сферы $R_k$ можно определять как среднее расстояние или как квадратный корень среднего квадратов расстояний объектов класса от центра эталона: $$R^2_k = \frac{1}{N_k}\sum^{N_k}_{i=1}\,(\mathbf{x}_i - \mathbf{c}_k)^2 ,~~~~~для~~~\mathbf{x}_i~\in~классу~k.$$ В качестве радиуса сферы можно также использовать расстояние максимально удалённого от центра $\mathbf{c}_k$ объекта.

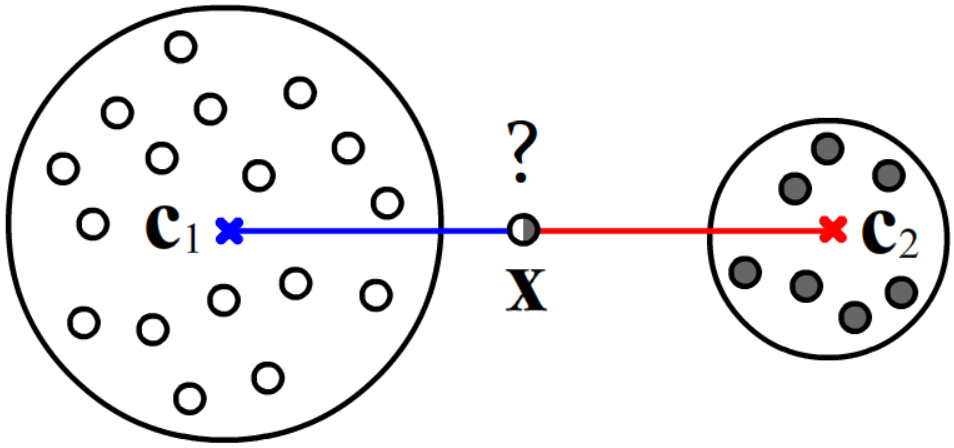
Если эталон $k$-го класса характеризуется положением $\mathbf{c}_k$ и радиусом сферы $R_k$, то можно уточнить решающее правило ($\ref{etal_dist}$). Например, пусть объекты двух классов в пространстве признаков занимают сферические области различных радиусов. Если классифицируемый объект находится на равных расстояниях от центров сфер, то его стоит отнести к тому классу, расстояние до поверхности сферы которого минимально. Так, на рисунке точку $\mathbf{x}$ следует считать белым, а не чёрным объектом. В связи с этим, напомним, что при равномерном распределении точек внутри $n$-мерной сферы, при больших $n$, случайно выбранная точка, почти наверняка окажется возле поверхности сферы.

Возможны следующие меры близости к эталону, которые используются в классификационном правиле: $$\frac{d(\mathbf{x},\mathbf{c}_k)}{R_k} = \mathrm{min},~~~~~~~~~или~~~~~~~~ d(\mathbf{x},\mathbf{c}_k) = \left\{ \begin{array}{ll} 0, & |\mathbf{x}-\mathbf{c}_k| \le R_k,\\ |\mathbf{x}-\mathbf{c}_k| - R_k, & |\mathbf{x}-\mathbf{c}_k| \gt R_k \end{array} \right. = \mathrm{min}.$$ Смысл первого правила обсуждается в следующем разделе. Второе правило предполагает, что, если точка попала в сферу эталона (всё равно на каком расстоянии от центра), то она принадлежит этому классу (расстояние нулевое), иначе берётся расстояние до поверхности сферы.

---

Эллиптические эталоны

Часто объекты класса "находятся внутри" эллипсоида (сплюснутой и повёрнутой сферы). Примером являются рукописные цифры (см. метод главных компонент). В этом случае лучше использовать расстояние Махаланобиса: $$d^2(\mathbf{a},\mathbf{b}) = \sum_{i,j} \bigr(a_i-b_i\bigr)\, C^{-1}_{ij}\, \bigr(a_j-b_j\bigr),$$ где $C^{-1}_{ij}$ - матрица, обратная к ковариационной матрице $C_{ij}=\langle(x_i-\bar{x}_i)(x_j-\bar{x}_j)\rangle$ и фигурные скобки означают усреднение по всем объектам данного класса.

Напомним, что собственные значения ковариационной матрицы $D_i$ - это дисперсии вдоль главных компонент (квадраты полуосей эллипсоида). Недиагональные компоненты матрицы характерезуют поворот эллипсоида. Уравнение эллипсоида имеет вид $d^2(\mathbf{x}, \mathbf{c})=1$, где $\mathbf{c}$ - центр его масс (вектор средних значений признаков данного класса).

Если координаты вектора признаков между собой статистически не связаны, то $C^{-1}_{ij}$ диагональна $\delta_{ij}/D_i$. Когда все $D_i$ равны $R^2$, мы имеем сферу и расстояние Махаланобиса эквиалентно правилу $d(\mathbf{x},\mathbf{c}_k)/R_k = \mathrm{min}$ с евклидовым расстоянием (см. предыдущий раздел). Рассмотрим геометрический смысл этого расстояния подробнее.

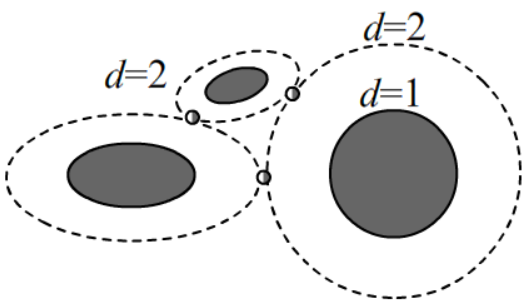
На плоскости $(x,y)$ уравнение эллипса с полуосями $\sigma_x=\sqrt{D_x}$ и $\sigma_y=\sqrt{D_y}$ и центром в начале координат имеет вид: $$\frac{x^2}{\sigma^2_x}+\frac{y^2}{\sigma^2_y} = d^2 = 1,$$ Если $d\gt 1$ - это уравнение растянутого в $d$ раз эллипса ($\sigma_x\mapsto d\cdot\sigma_x$, $\sigma_y\mapsto d\cdot\sigma_y$). Выше на рисунке исходные эллипсы, содержащие объекты, заштрихованы. Окружающие их пунктирные линии - это увеличенные в 2 раза исходные эллипсы. При использовании расстояния Махаланобиса предполагается, что точки касания (пересечения) пунктирных линий $d=const$ находятся на равном расстоянии $d$ от эллиптических эталонов.

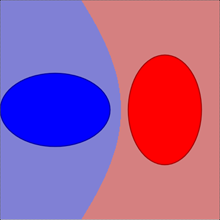
При больших размерностях $n$ пространства признаков, имеет смысл воспользоваться методом главных компонент (независимо для каждого класса). Пусть собственные векторы ковариационной матрицы равны $\mathbf{e}^{(i)}$. Ограничимся $m$ векторами, которые соответствуют максимальным собственным значениям $\lambda_1,...,\lambda_m$. Тогда: $$y_1=\frac{1}{\sqrt{\lambda_1}}(\mathbf{x}-\mathbf{c})\cdot\mathbf{e}^{(1)},~~...,~~y_m=\frac{1}{\sqrt{\lambda_m}}(\mathbf{x}-\mathbf{c})\cdot\mathbf{e}^{(m)},~~~~~~~~~~~~и~~~~~~~~~~~~d^2(\mathbf{x},\mathbf{c})=y^2_1+...+y^2_m.$$ Такое вычисление расстояния существенно быстрее, чем суммирование с обратной ковариационной матрицей.

---

Кластеризация эталонов

Вернёмся к сферическим эталонам. Если сферы сильно перекрываются или полностью поглощаются, то стоит увеличить число эталонов каждого класса (провести кластеризацию). Кластеризация обучающих объектов каждого класса проводится независимым образом.

Метод динамических средних является простейшим способом кластеризации. "Руками" задаём число кластеров $m$. В качестве начального положения центров кластеров $\mathbf{c}_1,...\mathbf{c}_m$ выбираем $m$ случайных примеров данного класса. Затем относим все $N_k$ примеров класса к ближайшему от них центру. Таким образом, каждому кластеру будет "принадлежать" $N_{k1}$,...,$N_{km}$ примеров. Положение $\mathbf{c}_i$ центра каждого кластера уточняется как центр масс попавших в него $N_{ki}$ точек: $$\mathbf{c}_i =\frac{1}{N_{ki}}\,\sum^{N_{ki}}_{j=1} \mathbf{x}_j,~~~~~~~~\mathbf{x}_j\in~классу~k~и~кластеру~i.$$ После этого процедура повторяется, пока положение кластеров не перестанет изменяться.

Размер кластера можно охарактеризовать дисперсией $D_i$ ($R_i=\sqrt{D_i}$ ) или расстоянием $R_i=R^{max}_i$ от центра самого удалённого объекта (из ближайших к этому кластеру). Характерный размер кластера также даёт корень суммы по-парных квадратов расстояний $S_k$ точек кластера (впрочем, её вычислять дольше, чем $D_i$ или $R^{max}_i$). $$D_i = \frac{1}{N_i}\,\sum^{N_i}_{j=1} d^2(\mathbf{x}_j,\mathbf{c}_j),~~~~~~~~~~~~S_i =\frac{1}{N_i\,(N_i-1)}\,\sum^{N_i-1}_{a=1}\sum^{N_i}_{b=a+1} d^2(\mathbf{x}_a,\mathbf{x}_b).$$

Качество кластеризации характеризует суммарная дисперсия по всем кластерам: $$\mathrm{Cost} = \sum^{m}_{i=1} D_i = \mathrm{min}.$$ Число кластеров $m$ необходимо увеличивать, пока Cost не перестанет заметно уменьшаться.

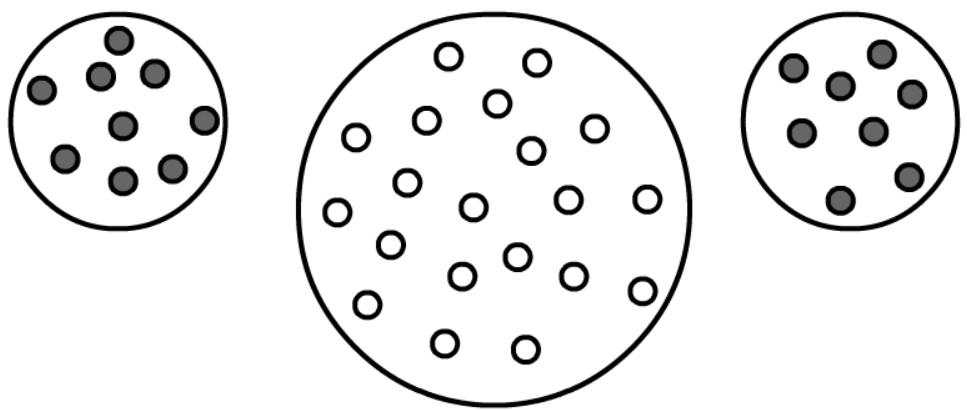
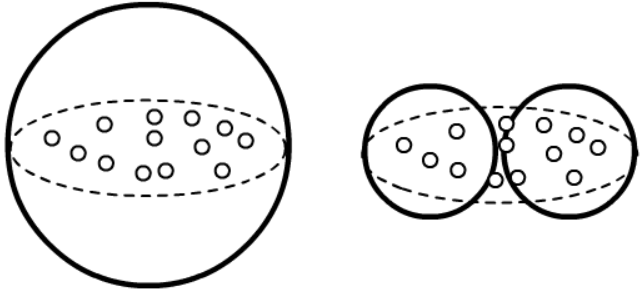На рисунке один кластер (левый) имеет радиус 2 (дисперсия $D=2^2=4$), тогда как два меньших кластера имеют единичные радиусы (дисперсия $D_1=D_2=1$). Соответственно, в первом случае Cost=4, а во втором - Cost=2.

При неудачном начальном выборе положения центров, алгоритм может сойтись не к глобальному минимуму Cost. Поэтому при данном $m$ его стоит перезапускать несколько раз. Поиграться c кластеризацией в 2-мерном пространстве признаков можно на этой странице.

Адаптивный алгоритм - более устойчивый метод кластеризации:

1. Начинаем с одного кластера в центре масс всех точек.
2. Находим самую удалённую точку от кластеров и делаем её новым кластером.
3. Раскидываем точки по кластерам и уточняем положения их центров методом динамических средних.
4. Goto 2, пока Cost не перестаёт уменьшаться.

После окончания кластеризации, можно отбросить кластеры, состоящие из одной точки, считая что такие объекты обучающего множества не информативны или шумовые.

Существует множество различных методов кластеризации, хорошие обзоры которых можно найти в [3] и [4].

---

Метод дробящихся эталонов

Будем характеризовать размеры кластеров $R_i$ максимальным расстоянием от центра $\mathbf{c}_i$ объектов, которые в этот кластер попали. Сферы кластеров, как одинаковых классов, так и разных могут перекрываться. В этом случае имеет смысл использовать метод дробящихся эталонов. Рассмотрим сначала следующие варианты пересечения сфер:

• (A) Кластер ни с кем не перекрывается или перекрывается с кластером того-же класса. Объекты классифицируются однозначно и дополнительно ни чего делать не надо.
• (B) Кластеры различных классов перекрываются, но в область перекрытия не попадают объекты. Тогда считаем, что перекрытие принадлежит сфере с меньшим радиусом (выше - это чёрный класс).
• (C) Если в область перекрытия попадают объекты только одного класса, тогда считаем это перекрытие принадлежащим тому же классу (выше - это белый класс).

Когда не выполнено ни одно из этих условий, необходимо отобрать объекты попавшие в область перекрытия и для них построить кластеры второго поколения:

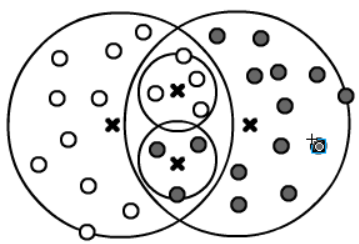
Далее процедура повторяется, пока все или почти все (при наличии шума) объекты не окажутся однозначно классифицируемыми.

Процедура распознавания применяется сперва к сферам первого уровня, причём выбираются те из них, которые окружают точку. Если их несколько, то к сферам второго уровня, и т.д. Если пример не попал ни в одну сферу, то используется критерий минимального расстояния до эталонов текущего уровня.

---

Метод ближайших соседей

Цель методов эталонов (да и всего машинного обучения) состоит в уменьшении числа входных примеров (сжатие информации), путём получения небольшого количества интегральных, эталонных образов. Противоположными к методам эталонов (в смысле сжатия информации) является группа методов в которых запоминают всю обучающую выборку.

При классификации данного объекта $\mathbf{x}$ изучают его непосредственное окружение в обучающей выборке и на его основании делают вывод о принадлежности примера к тому или иному классу.

Возможны различные модификации метода. В простейшем случае ищем ближайшую точку обучающего множества и берём при распознавании её класс. При наличии шума лучше отобрать $k$ ближайших соседей $d(\mathbf{x},\mathbf{x}_1)\le d(\mathbf{x},\mathbf{x}_2)\le...\le d(\mathbf{x},\mathbf{x}_m)$ и использовать класс, встречающийся чаще всего (голосование). Другая разновидность метода состоит в использовании соседей, попавших внутрь сферы некоторого радиуса.

Подбор параметров (число соседей, радиус), можно проводить методом LOO (leave-one-out). Для этого метод соседей применяется по-очереди к каждому объекту обучающей выборки и вычисляется ошибка классификации. Текущий объект в составе своих соседей, естественно, не учитывается.

---

Профиль компактности

Отметим важную характеристику обучающего множества, называемую профиль компактности. Это доля обучающей выборки (из $N$ объектов) у которой $m$-й сосед (по удалённости) лежит в другом классе: $$K(m) = \frac{1}{N}\sum^N_{\mu=1} \bigr[ Y_\mu \neq Y^{(m)}_\mu\bigr].$$ (квадратные скобки означают 1, если классы $\mu$-того объекта и его $m$-того соседа не совпадают; если совпадают - это ноль). Если профиль при малых $m$ близок к нулю, а после начинает резко расти, это означает, что классы в пространстве признаков хорошо разделимы. Другой крайний случай - это горизонтальная прямая для $K(m)$, означающая что мы имеем дело с очень плохо классифицируемыми данными.

Метод ближайших соседей при отсутствии ограничений на память и быстродействие является достаточно мощным, при очевидной простоте его реализации (lazy learning). Однако, он, вообще говоря, не обладает способностью к обобщению (сглаживанию), поэтому не всегда лучше метода дробящихся эталонов или разделяющих поверхностей (нейронные сети и т.п.)

---

Метод потенциальных функций

Метод потенциальных функций является разновидностью метода ближайших соседей, в котором вес класса соседа зависит от его расстояния до данной точки. Для $k$ ближайших соседей или для всех примеров данного класса вычисляем значение функции: $$\phi_k = \frac{1}{N_k} \sum^{N_k}_{i=1} \phi(\mathbf{x}-\mathbf{x}_i),~~~~~~\mathbf{x}_\in ~классу~k,$$ где суммирование ведётся по примерам $k$-того класса, а в качестве "потенциалов", создаваемых каждым примером $\phi(\mathbf{x}-\mathbf{x}_i)$, могут выступать функции ($a,\phi_0$ - параметры): $$\phi(r) = \frac{\phi_0}{1+(a r)^2},~~~~~~~~~~~~ \phi(r) = \phi_0\, e^{-(a r)^2},~~~~~~~~~~~\phi(r) = \frac{\phi_0}{e^{-a r}+e^{a r}}.$$ Подобные потенциальные функции строятся независимо для каждого класса. В качестве правила распознавания выбирается тот класс, чья потенциальная функция в данной точке имеет наибольшее значение.

Если обучающие объекты не зашумлены, потенциальные функции можно дополнительно обучать. Например, те примеры, которые не правильно распознались (по потенциалам остальных примеров), увеличивают свой вес ("заряд", генерирующий потенциал) $\phi_0 \to 2\phi_0$. Можно также менять параметр $a$ (скорость убывания потенциала) и т.д. Вместо вещественного параметра $a$ можно оптимизировать номер $m$-того соседа, положив $a=1/d(\mathbf{x},\mathbf{x}_m)$.

---

Отбор эталонных соседей

Не все объекты обучающего множества одинаково важны при классификации методом ближайших соседей или потенциальных функций. Часть объектов может оказаться шумом. Другая часть - избыточно сконцентрированными в некоторой области пространства признаков. Поэтому имеет смысл уменьшать обучающую выборку, формируя значимое обучающее подмножество эталонных объектов. Это делает методы ближайших соседей не такими уж и lazy learning. Рассмотрим два жадных алгоритма формирования подмножества эталонных объектов.

Отбрасывание худших. Перебираем все объекты обучающего множества. Текущий объект выбрасываем и методом LOO (leave-one-out) вычисляем ошибку классификации остальных объектов. Выброшенный объект возвращаем и повторяем процедуру. После окончания перебора, исключаем из обучающей выборки объект, отбрасывание которого приводило к минимальному изменению ошибки. Затем процедура повторяется, пока LOO - ошибка не начинает заметно расти. Оставшиеся в выборке объекты и являются эталонными.

Добавление лучших. Аналогично, но в множество эталонных объектов (первоначально пустое) добавляется объект, LOO ошибка исключения которого была максимальна.

Ниже нарисована модельная обучающая выборка для двух классов в 2-мерном пространстве признаков. Это пространство разбивается на две эталонные области, в которых в основном находятся объекты одного класса. Впрочем, в этих областях вкраплены шумовые объекты (один чёрный объект в классе белых и один белый в классе чёрных). Кроме этого, есть пограничная зона, в которой объекты двух классов сильно перемешаны. Такие объекты будут не информативны при распознавании. Шумовые вкрапления не только не информативны, но и вредны. Их исключение приведёт к уменьшению LOO - ошибки, так как их соседи перестанут неправильно классифицироваться.

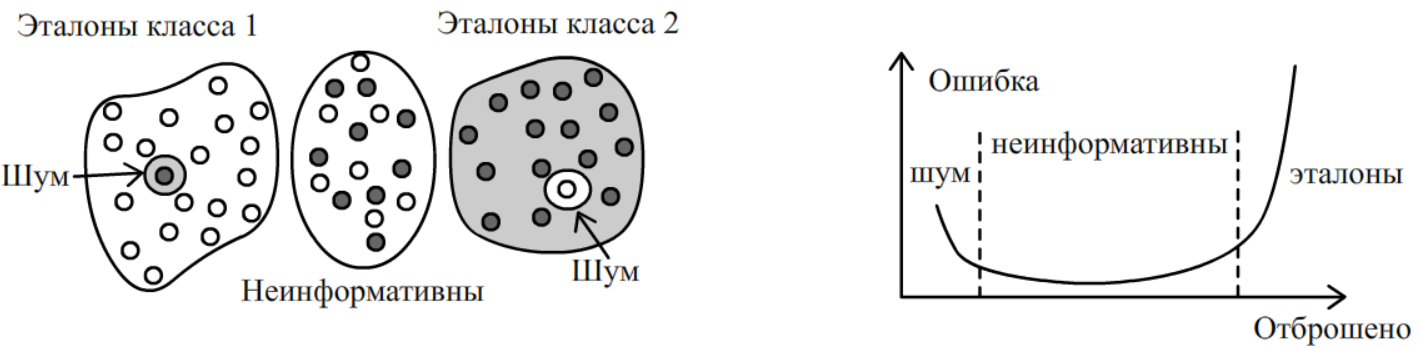
Справа дан график LOO - ошибки как функции числа отброшенных объектов в алгоритме "отбрасывание худших". В начале отбрасываются те объекты, которые заведомо являются шумовыми и ошибка снижается (перестают ошибаться соседи шумовых "вкраплений"). Затем очередь доходит до не информативных объектов, присутствие которых в обучающей выборке пользы для распознавания не приносит. Для них ошибка классификации выходит на плато. Наконец, когда алгоритм добирается до значимых (эталонных) объектов, график ошибки резко начинает расти. В этот момент необходимо остановиться.

Если эталонных объектов сравнительно не много, быстрее будет работать метод "добавления лучших". В противном случае эффективнее метод "отбрасывания худших".

---

Полезная информация

• [1] Загоруйко Н.Г. - "Прикладные методы анализа данных и знаний" (1999).
• [2] Воронцов К.В. "Машинное обучение" (курс лекций)
• [3] Воронцов К.В. "Лекции по алгоритмам кластеризации"
• [4] Интересные алгоритмы кластеризации
• Отрывок из семинара

---