Нейронные сети: 1. Основы

Введение

Этим документом начинается серия материалов, посвящённых нейронным сетям. Иногда к ним относятся по принципу: человеческая нейронная сеть может решать любые задачи, поэтому и достаточно большая искусственная нейронная сеть на это способна. Чаще всего архитектура сети и параметры её обучения являются предметом многочисленных экспериментов. Сеть при этом оказывается чёрным ящиком, происходящее в котором загадочно даже для её учителя.

Мы постараемся совмещать эмпирические советы и математическое понимания природы нейронов как разделяющих гиперплоскостей и функций нечёткой логики. Сначала будут рассмотрены различные модельные примеры двумерных пространств признаков. Наша цель - выработать интуитивное понимание выбора архитектуры сети. В дальнейшем мы перейдём к многомерным задачам, распознанию графических образов, свёрточным и рекуррентным сетям. Приведенные ниже примеры можно запустить, потренировавшись в подборе параметров обучения.

Объекты и их признаки

Пусть есть однотипные объекты (бутылки с вином, посетители в больнице, позиции на шахматной доске):

Каждый объект характеризуется набором (вектором) признаков x={x1,x2,...,xn}. Признаки могут быть:

Далее будем считать признаки вещественными числами из диапазона [0...1]. Этого всегда можно достичь при помощи нормировки, например: x -> (x-xmin)/(xmax-xmin). Бинарные признаки, соответственно, принимают значение 0 или 1. Нечисловые признаки, увеличив размерность вектора x, можно сделать бинарными (красный/не красный, синий/не синий). Кроме этого, пока будем считать, что объекты между собой причинно не связаны и их порядок не существенен.

Пусть объекты данного типа разбиваются на классы (человек: {здоровый, больной}, вино: {итальянское, французское, грузинское}). С каждым объектом можно также связать некоторое число y (степень преимущества белых в шахматной позиции; качество вина по усреднённому мнению экспертов и т.д.). Часто решаются следующие две, тесно связанные задачи:

Примеры:

Для успешного решения задач классификации или регрессии, признаки, характеризующие объект, должны быть значимыми, а вектор признаков - полным (достаточным для классификации объектов или определение регрессионной величины y ).

Однажды Джед и Нед захотели различать своих лошадей. Джед сделал на ухе лошади царапину. Но лошадь Неда поцарапала о колючку тоже самое ухо. Тогда Нед прицепил голубой бант на хвост своей лошади, но лошадь Джеда его сожрала. Фермеры долго размышляли и выбрали признак, который не так легко изменить. Они тщательно измерил высоту лошадей, и оказалось, что черная кобыла Джеда на один сантиметр выше белого жеребца Неда.

Обучение с учителем

Пусть есть множество объектов, каждый из которых принадлежит одному из k пронумерованных (0,1,2,...k-1) классов. На этом обучающем множестве, предоставленнным "учителем" (обычно человеком), система обучается. Затем, для неизвестных системе объектов (тестовом множестве), она проводит их классификацию, т.е. сообщает к какому классу принадлежит данный объект. В такой постановке - это задача распознавания образов после обучения с учителем.

Число признаков n называется размерностью пространства признаков. Пусть признаки лежат в диапазоне [0...1]. Тогда любой объект представим точкой внутри единичного n-мерного куба в пространстве признаков.

Распознающую систему представим в виде чёрного ящика. У этого ящика есть n входов, на которые подаются значения признаков x={x1,x2,...,xn} и k выходов y={y1,...,yk} (по числу классов). Значение выходов также будем считать вещественным числами из диапазона [0...1]. Система считается правильно обученной, если при подаче на входы признаков, соответствующих i-тому классу, значение i-того выхода равно 1, а всех остальных 0. На практике, такого результата добиться трудно и все выходы оказываются отличными от нуля. Тогда считается что номер выхода с максимальным значением и есть номер класса, а близость этого значения к единице говорит о "степени уверенности" системы.

Когда есть только два класса, ящик может иметь один выход. Если он равен 0, то это один класс, а если 1 - то другой. При нечётком распознавании вводятся пороги уверенности. Например, если значение выхода лежит в диапазоне y=[0 ... 0.3] - это первый класс, если y=[0.7 ... 1] - второй, а при y=(0.3 ... 0.7) система "отказывается принимать решение".

Ящик с одним выходом может также аппроксимировать функцию y=f(x1,...,xn), значения y которой непрерывны и обычно также нормируются на единицу, т.е. y=[0 ... 1]. В этом случае решается задача регрессии.

Нейрон

Нейронная сеть - одно из возможных наполнений чёрного ящика. Узел сети - это нейрон, имеющий n входов x={x1,x2,...,xn} и один выход y. С каждым входом связан вещественный параметр синаптического веса ω={w1,w2,...,wn}. Кроме этого, нейрон имеет также "параметр смещения" w0. Таким образом, любой нейрон с n входами полностью определяется n+1 параметром.

Выход нейрона вычисляется следующим образом. Значение каждого входа xi умножают на соответствующий ему синаптический вес wi и эти произведения складывают. К сумме добавляют параметр смещения w0. Результат d приводят к диапазону [0 ... 1] при помощи нелинейной сигмоидной функции y=S(d):

d = w0 + w1x1 + ... + wnxn,         y = S(d) = 1/(1+exp(-d)).

Сигмоидная функция стремится к 1 при больших положительных d и к 0 при больших отрицательных d. Когда d=0, она равна S(0)=0.5. Таким образом, нейрон это нелинейная функция n переменных порогового вида:

Сеть нейронов

Сеть является множеством соединённых между собой нейронов. Возможны различные способы соединения и, следовательно, различные архитектуры сети. Пусть нейроны располагаются слоями и значения выходов нейронов i-того слоя подаётся на входы всех нейронов следующего i+1 слоя. Такую сеть называют полносвязной сетью прямого распространения. Входы сети мы будем обозначать квадратиками и называть входными нейронами. В отличии от "обычных" нейронов - это просто линейная функция y=x. Выходы нейронов последнего слоя сети являются выходами чёрного ящика и обозначаются треугольниками.

Ниже на первом рисунке сеть состоит из трёх входов (нулевой слой) и двух выходных нейронов. Такую архитектуру будем кодировать следующим образом: [3,2], где цифры - это число нейронов в слое. Первая цифра - всегда количество входов, а последняя - количество выходов. На следующем рисунке представлена сеть [2,3,1]. Она содержит один скрытый слой с тремя нейронами. Он скрыт в том смысле, что находится внутри чёрного ящика (пунктир) между входным и выходным слоем (нейроны выходного слоя, впрочем, также частично скрыты и наружу "торчат" только их выходы). На третьем рисунке представлена сеть [2,3,3,2] с двумя скрытыми слоями.

Эти сети названы сетями прямого распространения потому, что данные (признаки объекта) подаются на вход и последовательно, без петель, передаются (распространяются) к выходам. К такому же типу сетей относятся т.н. свёрточные сети, в которых соединены между собой не все нейроны двух соседних слоёв (ниже первый рисунок). Часто при этом веса у всех нейронов свёрточного слоя одинаковые. Подробнее о таких сетях будет говориться при распознавании изображений. На втором рисунке ниже представлен вариант сети в которой понятие слоя отсутствует, однако это по-прежнему сеть прямого распространения.

Последний рисунок - это уже сеть не прямого распространения, а т.н. рекуррентная сеть. В ней сигналы с одного или нескольких выходных нейронов подаются обратно на вход. Обычно такая рекурсия, проводится в несколько циклов, пока на выходах сети не установятся стационарные значения. Рекуррентные сети обладают памятью и последовательность подачи объектов для них важна. Такое поведение полезно, если объекты упорядочены во времени (например при предсказании временных рядов).

Обучение любой сети состоит в подборе параметров w0,w1,...,wn каждого нейрона, таким образом, чтобы для данного объекта (подаём на входы сети x1,...,xn), выходы сети имели значения, соответствующие классу объекта.

Отметим, что, хотя нейрон всегда имеет только один выход, он может "подаваться" на входы различных нейронов. Аналогично, в живых нейронах аксон расщепляется на отдельные отростки, каждый их которых воздействует на синапсы ("точки соединения") дендридов других нейронов. Если нейрон возбудился, то это возбуждение передаётся по аксону к дендридам его соседей.

Нейрон как гиперплоскость

Чтобы чёрный ящик распознающей системы сделать прозрачнее, рассмотрим геометрическую интерпретацию нейрона. В n-мерном пространстве каждая точка задаётся n координатами (вещественными числами x = {x1,...,xn}). Плоскость (как и в обычном 3-мерном пространстве) задаётся вектором нормали ω={w1,...,wn} (перпендикуляр к плоскости) и произвольной точкой x0={x01,...,x0n}, лежащей в этой плоскости. Когда n > 3 плоскость принято называть гиперплоскостью.

Расстояние d от гиперплоскости до некоторой точки x={x1,...,xn} вычисляется по формуле

d = w0 + w1 x1 + ... + wn xn,     где     w0 = -(w1 x01 + ... + wn x0n).

При этом d > 0, если точка x лежит с той стороны плоскости, куда указывает вектор ω и d < 0, если с противоположной. Когда d = 0 - точка x лежит в плоскости. Это ключевое для дальнейшего изложения утверждение, которое стоит запомнить.

Изменение параметра w0 сдвигает плоскость параллельным образом в пространстве. Если w0 уменьшается, то плоскость смещается в направлении вектора ω (расстояние меньше), а если w0 увеличивается - плоскость смещается против вектора ω. Это непосредственно следует из приведенной выше формулы.

◄ Вывод этой формулы (который можно пропустить) проведём в векторных обозначениях. Запишем вектор x - x0, начинающийся в точке x0 (лежащей в плоскости) и направленный в точку x (см. рисунок справа; векторы складываются по правилу треугольника). Положение точки x0 выбрано в основании вектора ω, поэтому ω и x - x0 коллинеарны (лежат на одной прямой). Если вектор ω единичный (ω2=1), то скалярное произведение векторов x - x0 и ω равно расстоянию точки x до плоскости:

d = w·(x-x0) = -w·x0 + w·x = w0 + w·x.

Если длина w=|ω| вектора ω нормали к плоскости отлична от единицы, то d в w раз больше (w>1) или меньше (w<1 ) евклидового расстояния в n-мерном пространстве. Когда векторы x - x0 и ω направлены в противоположные стороны: d < 0. ►

Если пространство имеет n измерений, то гиперплоскость это (n-1)-мерный объект.
Она делит всё пространство на две части. Для наглядности рассмотрим 2-мерное пространство. Гиперплоскостью в нём будет прямая линия (одномерный объект). Справа на рисунке кружок изображает одну точку пространства, а крестик - другую. Они расположены по разные стороны от линии (гиперплоскости). Если длина вектора ω много больше единицы, то и расстояния d от точек к плоскости по модулю будут существенно большими единицы.

Вернёмся к нейрону. Несложно видеть, что он вычисляет расстояние d от точки с координатами x=(x1,...,xn) (вектор входов) до гиперплоскости (w0, ω). Параметры нейрона ω=(w1,...,wn) определяют направление нормали гиперплоскости, а w0 связан со смещение плоскости вдоль вектора ω. На выход нейрона подаётся нормированное на диапазон [0...1] расстояние S(d). При больших wi объект, нарисованный выше кружком, приведёт к выходу нейрона близкому к единице, а крестик - к нулю. Отношение w0/|ω| равно расстоянию от плоскости до начала координат (0,...,0). По модулю оно не должно превышать n½

1. Нейрон является гиперплоскостью. Значение его выхода равно нормированному расстоянию от вектора входов до гиперплоскости. В процессе обучения, плоскость каждого нейрона меняет свою ориентацию и сдвигается в пространстве признаков.

Уверенность нейрона

При обучении сети необходим критерий, в соответствии с которым подбираются параметры нейронов. Обычно для этого служит квадрат отклонения выходов сети от их целевых значений. Так, для двух классов и одного выхода, ошибкой Error сети считаем

Error2 = (1/N) ∑ (y-yc)2 ,

где y - фактический выход, а yc - его правильное значение, равное 0 для одного класса и 1 - для второго. Сумма ведётся по N обучающим примерам. Эту среднеквадратичную ошибку по всем обучающим объектам стараются сделать минимальной. Методы минимизации ошибки (подбор параметров нейронов) мы обсудим позднее.

Рассмотрим 2-мерное пространство признаков x1,x2 и два класса 0 и 1. На рисунке ниже объекты одного класса представлены синими кружочками, а объекты второго класса - красными крестиками. Справа от пространства признаков приведена сеть [2,1] из одного нейрона. За ней, на сине-красном квадратике, нарисована карта значений выхода нейрона при тех или иных входах (x1,x2 пробегают значения от 0 до 1 с шагом 0.01). Если y=0 - то это синий цвет, если y=1 - то красный, а белый цвет соответствует значению y=0.5:

σ=0.2D

Справа от рисунков под чертой, в квадратных скобках даны параметры нейрона: [w0,w1,w2]. В круглых скобках приведена длина |w| вектора нормали ω и среднее значение выхода <y> и его волатильность σy (см. ниже). Ось x1 пространства признаков направлена вправо, а ось x2 - вниз. Поэтому вектор ω с положительными компонентами {w1, w2} направлен по диагонали вниз (он нарисован рядом с кружочком на прямой, содержащим номер нейрона 1).

Над чертой в таблице приведена среднеквадратичная ошибка Error такой сети. При этом строка Learn означает обучающую последовательность объектов, а Test - проверочную, которая не участвовала в обучении (тестовые объекты на графике пространства признаков изображены полупрозрачными). Колонка Miss содержит процент неправильно распознанных сетью объектов (отнесённых не к своему классу). Последняя строка kNear означает ошибку и процент ошибок в методе 10 ближайших соседей (он будет описан позднее).

В этом примере разброс признаков объектов каждого класса невелик. Классы легко разделяются гиперплоскостью (линией в 2-мерии). Сеть стремиться минимизировать ошибку к целевым значениям 0 или 1 на выходе, поэтому модуль вектора |w|=48 принимает сравнительно большое значение. В результате, даже недалеко расположенные от плоскости объекты (в обычном евклидовом смысле) получают большое по модулю значение d. Соответственно y=S(d) = 0 или 1. Такой нейрон мы будем называть уверенным. Чем больше |w|, тем более уверен в себе нейрон. На его карте выхода тонкая белая линия (область неуверенности) отделяет насыщенный синий цвет (один класс) от насыщенного красного цвета (второй класс).

Несколько иная ситуация во втором примере, где существует широкая область перекрытия объектов различных классов. Теперь нейрон не столь уверен в себе и длина вектора |w|=24 в 2 раза меньше:

σ=D
σ=D

Приведём функции деформации расстояния (сигмоид) при длине вектора нормали, равной 1,2,5,10,100:

Так как входы нейрона нормированы на единицу, максимальное расстояние от точки x с координатами {x1,...,xn} в n-мерном кубе (его диагональ) равна корню из n. В 2-мерном пространстве признаков dmax=1.4. Если плоскость проходит через середину куба dmax~0.5.

Уверенный нейрон - не всегда хороший нейрон. Если размерность пространства признаков n велика, а обучающих данных N мало, сеть состоящая из уверенных нейронов может оказаться переобученной и на тестовых объектах приводить к большой ошибке распознавания. Кроме этого самоуверенные нейроны медленнее обучаются. Подробнее мы остановимся на этих вопросах ниже.

В заключение сформулируем главный вывод, справедливый для пространств любой размерности:

2. Если два класса в пространстве признаков разделяются гиперплоскостью, то для их распознавания достаточно одного нейрона.

Полезность нейрона

В случае, если гиперплоскость нейрона не пересекает единичный гиперкуб в котором находятся признаки (или значения выходов предыдущих нейронов), то от такого нейрона обычно мало пользы. Он не разделяет на две части входные данные (которые всегда принадлежат интервалу [0 ... 1]. Такой нейрон будет называться бесполезным.

Необходимо стремиться к тому, чтобы все нейроны сети были полезными. Иногда бесполезность появляется и для плоскости, пересекающей гиперкуб, если объекты любых классов оказываются с одной стороны этой плоскости.

Перед началом обучения параметры нейронов полагают равными случайным значениям. При этом нейрон может сразу оказаться бесполезным. Чтобы этого не произошло, можно использовать следующий алгоритм инициализации:

Компоненты вектора ω задаём случайным образом, например в диапазоне [-w ... w], где w ~ 1 - 10. Затем, внутри единичного гиперкуба (или в некоторой его центральной части), выбираем случайную точку x0={x01,...,x0n}. Параметр сдвига задаём следующим образом: w0 = -ω·x0 = -(w1x01 + ... + wnx0n). В результате гиперплоскость будет гарантированно проходить через гиперкуб.

Параметр сдвига стоит контролировать и в процессе обучения, так чтобы нейрон был всё время полезным. Здесь возможны два способа - геометрический и эмпирический. В эмпирическом вычисляется среднее значение выхода каждого нейрона по обучающим объектам. Если после прохождения через сеть всех обучающих примеров, средние значения <y> некоторых нейронов близки к нулю или единице, то они считаются бесполезными. В этом случае их можно "встряхнуть" случайным образом (возможно с сохранением вектора ω, изменяя только параметр сдвига w0).

На всех примерах в этом документе нейроны в сетях разукрашены в соответствии со значением их <y>. Если <y> = 0.5, то нейрон белый, если <y> = 0 - синий, а если <y> = 1 - красный. Насыщенный синий или красный цвета означают бесполезность нейрона. В первых двух примерах, единственный нейрон получился очень полезным (белым), так как объекты классов равновероятно находились справа и слева от линии (разделяющей гиперплоскости).

Кроме среднего значения выхода, важную роль играет волатильность нейрона σy, равная среднеквадратичным отклонениям его выхода от среднего значения <y>. Чем волатильность меньше, тем менее полезен нейрон. Действительно, в этом случае, не зависимо от значений входов, он принимает одно и то же значение на выходе. Поэтому, без изменения выходных значений сети, такой нейрон можно выбросить, сдвинув соответствующим образом параметры нейронов, для которых бесполезный нейрон является входным.

Несколько выходов

Рассмотрим теперь 3 класса. Использовать один нейрон не очень удобно, поэтому, как было описано в начале документа, создадим сеть [2,3] с тремя выходами. Пусть классы локализованы в пространстве признаков следующим образом:

Каждый выходной нейрон отделяет "свой класс" от остальных двух. Например, первый сверху нейрон (на рисунке горизонтальная плоскость номер 1) распознаёт объекты, помеченные синими кружочками, выдавая на выходе 1, если объект находится с той стороны, куда направлен вектор ω (чёрточка рядом с номером плоскости).

Аналогично, второй нейрон распознаёт красные крестики, а третий - зелёные квадратики. В каждом случае векторы нормали направлены в сторону "своих" классов. Все нейроны сети достаточно уверенны в себе и вполне полезны. Их небольшая синева связана с тем, что против вектора нормали всегда расположено вдвое больше данных ("чужих" двух классов), чем по вектору. Поэтому среднее значение каждого выхода смещено ниже нейтрального уровня 0.5.

Когда нужен скрытый слой

Перейдём теперь к чуть более сложной задаче. Пусть объекты двух классов (кружочки и крестики) сосредоточены по углам пространства признаков так, как на рисунке справа. Одной гиперплоскостью (линией) эти два класса разделить нельзя. Иногда такую задачу называют разделяющим ИЛИ (xor). Эта логическая операция равна истине (единице) только, если один из аргументов равен истине, а второй лжи (нулю): "Маша любит или Колю или Васю, но не их обоих". На рисунке классу, помеченными кружками, на выходе сеть должна выдавать ноль, а классу крестика - единицу. Если объекты находятся точно в углах, то xor(0,0) = xor(1,1) = 0 и xor(0,1) = xor(1,0) = 1.

Чтобы провести классификацию, необходима нейронная сеть [2,2,1] с одним скрытым слоем. Ниже на первом графике (в осях признаков x1 и x2) показаны две гиперплоскости (линии A и B). Они соответствуют двум скрытым нейронам A и B. Значения выходов нейронов приведены на втором графике (оси yA и yB).

Оба крестика лежат по направлениям векторов нормалей плоскостей A и B. Поэтому расстояние от них к плоскостям будет положительным и, если нейроны достаточно уверены в себе, на их выходах yA и yB будет получаться единица (нижний правый угол плоскости yA, yB).

Кружок с признаками (0,0) из верхнего левого угла плоскости x1, x2 даст на выходах нейронов yA~0, yB~1 (этот объект лежит против вектора нормали плоскости A и по вектору нормали плоскости B). Второй кружок с признаками (1,1) даст на выходах нейронов значения yA~1, yB~0. Получившееся "деформированное" пространство признаков yA и yB (второй график) уже легко разделить одной плоскостью C, которая и будет выходным нейроном сети. Если вектор её нормали направлен так как указано на втором графике, то для обоих крестиков получится y~1, а для кружков y~0.

Ниже приведен реальный пример нейронной сети, обученной распознавать два класса объектов, каждый из которых разбивается на два кластера:

3. Каждый слой сети преобразует входное пространство признаков в некоторое другое пространство, возможно, с иной размерностью. Такое нелинейное преобразование происходит до тех пор, пока классы не оказываются линейно разделимыми нейронами выходного слоя.

Нейроны как логические элементы

К анализу поведения нейронов можно подойти с позиций математической логики. Для этого сконцентрируемся на одном классе задачи xor, например на крестиках. Запишем логическое условие которому удовлетворяют все объекты этого класса. В примере выше: "любой крестик лежит по вектору плоскости A и по вектору плоскости B". Это кратко можно выразить формулой A & B. Выходной нейрон "C" реализует такое логическое "И". Действительно, его плоскость прижата к правому нижнему углу квадрата в пространстве признаков с координатами (1,1). Поэтому для входов (поставляемых нейронами "A" и "B") близких к единице, на выходе этого нейрона будет 1 (точнее его значение больше 0.5). Поэтому, как и положено, 1 & 1 = 1. Если хотя бы один из входов отличен от 1, то и выход будет нулевым (меньшим 0.5). Это справедливо и в пространстве произвольной размерности, где гиперплоскость нейрона, обеспечивающего логическое "И" прижата к углу гиперкуба с координатами (1,1,...,1) (отсекает его от остального гиперкуба).

Если плоскость сместить в угол (0,0), сохранив направление нормали к углу (1,1), то такой нейрон будет логическим "ИЛИ". Его функция y=S(x1,x2) даёт S(0,0)=0 и в остальных случаях 1 (ниже первый рисунок):

В общем случае, плоскость нейрона, реализующего логическое "ИЛИ" отсекает угол (0,0,...,0) n-мерного куба, а вектор его нормали направлен в сторону большего объём гиперкуба. В отличии от этого, стандартное логическое "И" (второй рисунок) имеет вектор нормали в сторону меньшего объёма.

Логическое "И" для нейрона с n входами описывается следующей функцией:

y = S( w·(x1+...+xn+α-n) ),      y = x1 & x2 & ... & xn,

где параметр α - параметр, лежащий в диапазоне 0<α<1. Чем он ближе к нулю, тем сильнее плоскость прижата к углу с координатами (1,1,...,1). Действительно, когда α=0 и x1=...=xn=1, имеем x1+...+xn-n=0. Чтобы этот нейрон обеспечивал логическое И, он должен давать отрицательное расстояние к "ближайшему" углу гиперкуба у которого одна координата равна нулю: (1,...,1,0,1,...,1). Это даёт ограничение α<1. Общий множитель w характеризует длину нормали (чем он больше, тем более уверен в себе нейрон). Сигмоидная функция S(d) приведена в начале документа.

Аналогично записывается функция логического "ИЛИ" (0<α<1)

y = S( w·(x1+...+xn-α) ),     y = x1 ∨ x2 ∨ ... ∨ xn.

Ещё одна логическая функция отрицания реализуется при помощи вычитания. Обозначим её чертой над именем переменной. Тогда x = 1-x и, как обычно, 0=1, 1=0. Если один из входов нейронов имеет отрицание, то его функция выхода имеет вид:

y = S( w·(-x1+...+xn+α-n+1) ),     y = x1 & x2 & ... & xn.

Таким образом, одна из компонент вектора нормали меняет свой знак и плоскость нейрона сдвигается. Выше на третьем и четвёртом рисунках приведены различные отрицания перменных. Стоит в этих терминах получить логическое ИЛИ из логического И при помощи правила де-Моргана:

!(x1 & x2) = x1 ∨ x2,

где восклицательный знак - ещё один способ обозначения логического отрицания.

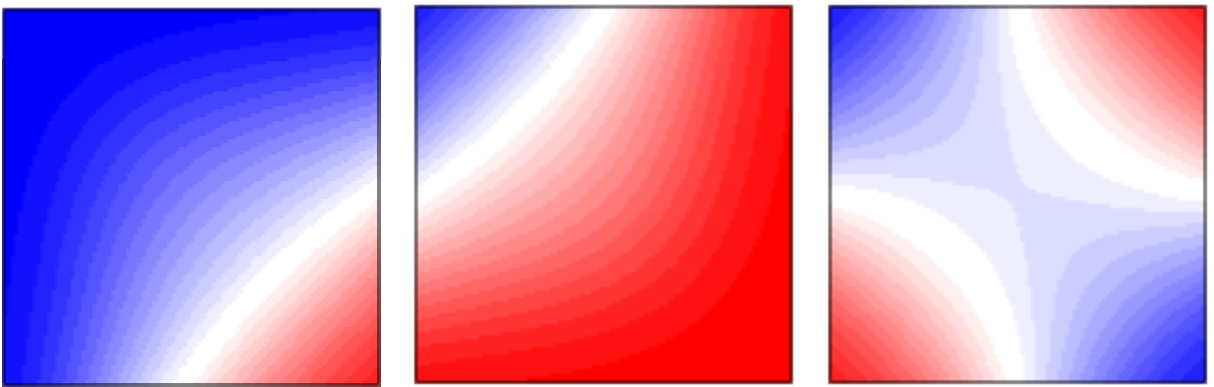
Четыре варианта xor

В качестве упражнения, стоит проанализировать 4 различных реализаций бинарной функции xor при помощи нейронных сетей:

Последний ряд картинок - это карты выхода реально обученных нейронных сетей, имеющих разделяющие плоскости на первом скрытом слое такие, как приведено в первом ряду картинок.

Аппроксимация функции y=f(x)

При помощи нейронной сети с одним входом, одним выходом и достаточно большим скрытым слоем, можно аппроксимировать любую функцию y=f(x). Для доказательства, создадим сначала сеть, которая на выходе даёт 1, если вход лежит в диапазоне [a...b] и 0 - в противном случае.

Пусть σ(d) = S(ω·d) - сигмоидная функция, аргумент которой умножен на большое число ω, так что получается прямоугольная ступенька. При помощи двух таких ступенек, можно создать столбик единичной высоты:

Нормируем аппроксимируемую функцию y=f(x) на интервал [0...1] как для её аргумента x, так и для значения y. Разобъём диапазон изменения x=[0...1] на большое число интервалов (не обязательно равных). На каждом интервале функция должна меняется незначительно. Ниже приведено два таких интервала:

Каждая пара нейронов в скрытом слое реализует единичный столбик. Величина d равна w1, если x∈(a,b) и w2, если x∈(b,с). Если выходной нейрон является линейным сумматором, то можно положить wi=fi, где fi - значения функции на каждом интервале. Если же выходной нейрон - обычный нелинейный элемент, то необходимо пересчитать веса wi при помощи обратной к сигмоиду функции (последняя формула).

Аппроксимация функции на Phyton

Ниже приведен код на языке Phyton, который аппроксимирует функцию y=sin(pi*x):

import numpy as np                    # библиотека численных методов
import matplotlib.pyplot as plt       # библиотека рисования графиков
         
def F(x):                             # эту функцию аппроксимируем
    return np.sin(np.pi*x);
 
n=10                                  # число интервалов
x1 = np.arange(0,   1,     1/n)       # координаты левых границ
x2 = np.arange(1/n, 1+1/n, 1/n)       # координаты правых границ
print("x1:",x1,"\nx2:",x2)            # выводим эти массивы
 
f  = F( (x1+x2)/2 )                   # функция в середине интервала
fi = np.log( f/(1-f) )                # обратные значения к сигмоиду
 
def S(z, z0, s):                      # сигмоид
    return 1/(1+np.exp(-100*s*(z-z0)))
 
def Net(z):                           # выход сети
    return 1/(1+np.exp(-np.dot(fi, S(z, x1, 1) + S(z, x2, -1) -1)))
 
x = np.arange(0.01, 1, 0.01)          # массив x-ов
y = [ Net(z)  for z in x ]            # массив y-ов (выход сети)
 
plt.plot(x, y)                        # результаты работы
plt.plot(x, F(x))                     # исходная функция
plt.show()                            # показываем картинку

В результате работы, при n=10 и n=100 получаются следующие результаты:

Нечёткая логика

Интерпретация нейронов как логических элементов в дальнейшем упростит анализ архитектуры нейронных сетей. Кроме этого, существует замечательная возможность реализовывать при помощи нейронных сетей системы, оперирующие с нечёткой логикой. В такой логике, кроме истины (1) и лжи (0) существует непрерывный диапазон истинностных значение от 0 до 1:

Сумка
симпотная		ДорогаяКрасного
цвета		Такая есть
у подруги		Моя машина
красная		У меня
депрессия		Покупаю
эту сумку!
x1x2x3x4x5x6y
1.00.01.0 1.0 0.00.00.0
1.01.01.0 0.0 1.00.01.0
0.50.50.5 0.5 0.51.01.0

Пусть свойствами объектов являются бинарные значения ("да", "нет"). А выход чёрного ящика y может принимать непрерывные значения. В ряде случаев они также равны 0 ("нет") или 1 ("да"). Однако при некоторых входах, выход может равняться, например, 0.5 ("возможно"). Нейронная сеть, наученная на подобных примерах, будет выдавать как бинарные рекомендации, так и выражать степень своей неуверенности.

Ниже приведены функции, которые принято использовать в нечёткой логике и их аппроксимация (задача регрессии!) при помощи нейронной сети:

and(x1,x2)= x1*x2
or(x1,x2)= x1+x2-x1*x2
xor(x1,x2)= or(and(x1,1-x2),and(1-x1,x2))

Мы вернёмся к нечёткой логике позднее.
> Нейронные сети: 2. Разделяющие поверхности