Теория вещества: 2. Основы термодинамики
Введение
В предыдущем документе мы рассмотрели модель идеального газа.
В равновесном состоянии такой газ, состоящий из N молекул, находящихся в объёме V,
характеризуется давлением P и температурой T.
Эти величины связаны уравнением состояния, а внутренняя энергия U газа пропорциональна
его температуре:
PV = NkT, U = NkTγ−1 = NfΘ2,
где параметр γ для одноатомных молекул равен 5/3 и связан с числом степеней свободы молкул f=3
и Θ=kT.
Если газ является смесью различных молекул числом N1,N2,..., то в уравнении
состояния N=N1+N2+..., а внутренняя энергия является суммой внутренних энергий каждой компоненты.
Температура T характеризует среднюю кинетическую энергию поступательного движения молекул
и в равновесии одинакова для тел, находящихся в тепловом контакте.
Теперь мы будем рассматривать произвольные термодинамические системы, используя идеальный газ как простейшую модельную систему, иллюстрирующую общие принципы.
Внутренняя энергия реальных термодинамических систем определяется не только кинетической энергией, но и взаимодействием между молекулами и внешними полями: U=N∑i=1Ti+∑i<jU(xi,xj)+N∑iV(xi), где Ti - кинетическая энергия, U(xi,xj) - потенциал парного взаимодействия двух молекул и V(xi) - потенциал молекулы во внешнем поле. Понятно, что уравнение состояние такой системы оказывается существенно более сложным, чем у идеального газа. Однако, общие принципы поведения всех этих систем достаточно схожи.
Нулевое начало термодинамики
Равновесное состояние на микроуровне является динамическим и "поддерживается" постоянным движением большого числа молекул. Время перехода в равновесное состояние называется временем релаксации τ.
Переменные состояния - это макроскопические величины типа T,P,V, которые полностью описывают термодинамическую систему на макроуровне в равновесном состоянии.
Равновесный процесс - это медленное изменение переменных состояния на каждом этапе которого система успевает прийти в равновесное состояние. Изображение кривой процесса на плоскости (P,V) обычно подразумевает, что это равновесный процесс (иначе нет смысла говорить о едином значении давления). Время изменения Δt переменных состояния в равновесном процессе должно существенно превышать время релаксации системы: Δt≫τ.
Процесс обратим когда возможен обратный переход из конечного состояния в начальное, через те-же промежуточные состояния. Равновесные процессы всегда обратимы. Однако существуют очень медленные изменения, которые не являются обратимыми (например, пластическая деформация). Необратимыми процессами также являются быстрые изменения переменных состояние. Подобным процессам посвящен следующий документ.
Первое начало термодинамики
 Любая замкнутая система характеризуется своей внутренней энергией U.
Любая замкнутая система характеризуется своей внутренней энергией U.Внутренняя энергия увеличивается при получении тепловой энергии δQ и уменьшается при совершении системой работы δA=PdV: dU = δQ − δA.
Тепловая энергия поступает (δQ>0) в систему при её контакте с более горячим телом или покидает (δQ<0) систему при контакте с более холодным телом (если δA=0). Работа δA=PdV, выполненная системой при расширении газа, уменьшает внутреннюю энергию (если δQ=0). При сжатии газа (δA<0) внутренняя энергия увеличивается (для этого необходимо затратить работу со стороны внешних сил).
Закон сохранения энергии, записанный в такой форме, называют первым началом термодинамики. Он имеет очень широкую область применимости и справедлив для любой системы находящейся, как в равновесии, так и вдали от него.
Переменные состояния
Любая функция переменных состояния f(P,V) является переменной состояния. Интегрирование её дифференциала df(P,V) = ∂f∂PdP+∂f∂VdV, ∂2f∂P∂V = ∂2f∂V∂P, 2∫1df(P,V)=f(P2,V2)−f(P1,V1). не зависит от пути на плоскости (P,V) и определяется только начальной и конечной точкой. Например поэтому Θ=PV/N или U=PV/(γ−1) являются переменными состояния, т.е. характеризуют текущее состояние системы, независимо от того, как она в него попала.
В термодинамике величины могут зависеть от различных переменных состояния. Поэтому при записи частных производных принято указывать какие величины при дифференцировании постоянны. Например, следующие производные в общем случае между собой не совпадают: (∂U∂P)VN ≡ ∂U(P,V,N)∂P, (∂U∂P)TN ≡ ∂U(P,T,N)∂P. Так, для идеального газа U=NkT/(γ−1)=PV/(γ−1), первая производная равна V/(γ−1), а вторая - нулю.
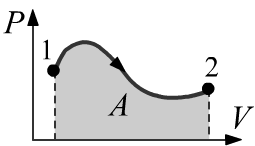 Работа A и теплота Q не являются переменными состояния так как
они зависят от способа перехода в данное состояние.
Для работы δA = PdV, выполняемой газом, это очевидно, т.к. её значение на плоскости (P,V)
равно интегралу от P(V)dV (площадь). Начальная и конечная точки
(состояния системы) могут быть соединены разными кривыми (процессами),
чему будет соответствовать различная работа. Так как δQ=dU+δA,
то и получаемая или отдаваемая системой теплота также зависит от характера процесса.
Поэтому говорить о накопленных телом в данном состоянии работе или теплоты ("теплород")
бессмысленно.
Работа A и теплота Q не являются переменными состояния так как
они зависят от способа перехода в данное состояние.
Для работы δA = PdV, выполняемой газом, это очевидно, т.к. её значение на плоскости (P,V)
равно интегралу от P(V)dV (площадь). Начальная и конечная точки
(состояния системы) могут быть соединены разными кривыми (процессами),
чему будет соответствовать различная работа. Так как δQ=dU+δA,
то и получаемая или отдаваемая системой теплота также зависит от характера процесса.
Поэтому говорить о накопленных телом в данном состоянии работе или теплоты ("теплород")
бессмысленно.
Принято использовать обозначение df для бесконечно малых величин, которые являются полными дифференциалами (и переменными состояния) и обозначение δg для малых величин не являющихся полным дифференциалом (таковы работа и теплота).
 Все переменные состояния делятся на два класса относительно их поведения при мысленном разделении
пространственно-однородной системы на части.
Для аддитивных переменных Fобщ = F1+F2.
Для неаддитивных: fобщ = f1 = f2.
Все переменные состояния делятся на два класса относительно их поведения при мысленном разделении
пространственно-однородной системы на части.
Для аддитивных переменных Fобщ = F1+F2.
Для неаддитивных: fобщ = f1 = f2.
Аддитивные переменные состояния пропорциональны числу молекул при их фиксированной концентрации n=N/V или их удельном объёме v=V/N (объём на одну молекулу). Примерами таких переменных являются объём V, число частиц N и внутренняя энергия U. В переменных (T,V) для аддитивных переменных выполняется следующее соотношение: F(T,V,N) = N⋅f(T,V/N).
Давление P и температура T - это неаддитивные переменные состояния (их также называют "интенсивными"). Они не зависят явно от числа молекул и других аддитивных переменных (зависят только от неаддитивных): F(T,V,N) = f(T,V/N). Например, давление идеального газа P = kT(N/V) = kTn не зависит от числа молекул (только от их концентрации n). В тоже время аддитивная внутренняя энергия явным образом пропорциональна числу молекул: U = NkT/(γ−1). Любые удельные величины в расчёте на одну частицу - неаддитивны (удельный объём v=V/N, удельная энергия u=U/N, удельная теплоёмкость c=C/N, см. ниже, и т.д.).
Естественно, вместо переменных (T,V,N) можно использовать другие, например (P,U,N). Тогда, например, для аддитивных величин будет: F(P,U,N)=Nf(P,U/N).
Переменные состояния обычно вычисляются в статистическом предельном переходе: N→∞, V=vN, v=1n=const. Термодинамическое состояние системы в таком пределе не зависит от свойств поверхности сосуда и его формы). Действительно, пусть L - линейные размеры сосуда и V∼L3. Число молекул у стенок в слое шириной D≪L по порядку равно nDL2<∼nL2∼(nV)2/3∼N2/3. Отношение числа молекул "чувствующих" свойства поверхности к их общему числу ∼N2/3/N=N−1/3≪1. Объём сложной формы всегда можно разбить на макроскопические объёмы простой формы, имеющие в пределе N→∞ одинаковые параметры состояния.
Теплоёмкости
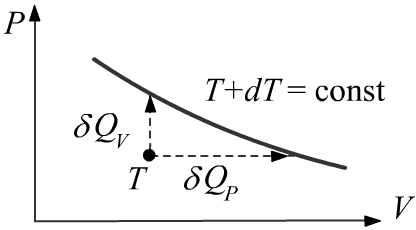 Передача тепла δQ системе может изменить её температуру dT.
Соответствующее отношение C=δQ/dT называется теплоёмкостью.
Чем больше система, тем больше её теплоёмкость.
Поэтому вводят понятие удельной теплоёмкости,
равной
отношению теплоёмкости к числу частиц c=C/N или к массе тела c=C/m.
Передача тепла δQ системе может изменить её температуру dT.
Соответствующее отношение C=δQ/dT называется теплоёмкостью.
Чем больше система, тем больше её теплоёмкость.
Поэтому вводят понятие удельной теплоёмкости,
равной
отношению теплоёмкости к числу частиц c=C/N или к массе тела c=C/m.
Теплоёмкость зависит от условий при которых тепло сообщается системе. Например, теплоёмкости при постоянном объёме CV и постоянном давлении CP для идеального газа не зависят от температуры и имеют следущие значения: CV = (δQdT)V δA=0 = (dUdT)V = kNγ−1, CP = (δQdT)P = [d(U+PV)dT]P = γγ−1kN. Связь CP = CV + kN называется соотношением Майера (теплоёмкость одного моля CP больше CV на газовую постоянную R=kNA≈8.31Дж/моль⋅K). То, что CP>CV типично для большинства термодинамических систем, так как, если V≠const, то при нагреве dT увеличивается внутренняя энергия и совершается работа.
Для идеального газа теплоёмкость CV является коэффициентом пропорциональности между внутренней энергией и его температурой, а отношение CP/CV определяет параметр γ: U=CVT, CPCV=γ>1.
В терминах степеней свободы f теплоёмкость CV=(f/2)kN и не зависит от температуры. Для реальных газов это не так. Например, для двухатомного водорода H2 при низких температурах параметр f=3. При повышении температуры он увеличивается и выходит на плато с f=5. Наконец при очень высоких температурах f=7. Такое поведение объясняет квантовая механика как активизацию колебательных Eкn=ℏω(n+1/2) и вращательных Eвn=ℏn(n+1)/2J уровней энергии (Eв∼Eк/100) с ростом температуры (молекулы "сильнее сталкиваются").
Калорическим уравнением состояния называется зависимость теплоёмкости при постоянном объёме от переменных состояния (T,V,N). Фактически это уравнение с точностью до константы определяет внутреннею энергию системы: CV = (dUdT)VN = N⋅c(T,V/N). Калорическое уравнение, вместе с уравнением состояния P = p(T,V/N) позволяет вычислить любые параметры произвольной системы. Напомним, что CV - это аддитивная величина (как и внутренняя энергия U), а давление P неаддитивно. В силу уравнения состояния, для описания системы достаточно только пары переменных состояния из списка {P,V,T}.
🔥 Найдём связь между теплоёмкостями CV,CP и уравнением состояния P=P(T,V) в общем случае. Изменение внутренней энергии U=U(T,V) равно: dU = (∂U∂T)VdT + (∂U∂V)TdV. Деля на dT и смещаясь вдоль кривой P=const на плоскости (T,V), имеем: (∂U∂T)P = (∂U∂T)V⏟CV + (∂U∂V)T(∂V∂T)P. Учитывая это соотношение и по определению теплоёмкости при постоянном давлении, получаем: CP=[d(U+PV)dT]P = CV + [(∂U∂V)T + P](∂V∂T)P. Чтобы выразить производную (∂V/∂T)P через функцию состояния P=P(T,V), учтём постоянство давления в определении теплоёмкости CP, которое означает: dP=0 = (∂P∂T)VdTP + (∂P∂V)TdVP, где dTP, dVP - это не произвольные приращения, а такие приращения, при которых давление остаётся неизменным (для этого должен "синхронно" изменяться и объём). Такие сдвиги на плоскости (T,V) должны происходить вдоль кривых P=P(T,V)=const. Из этого соотношения сразу следует: (∂V∂T)P = −(∂P/∂T)V(∂P/∂V)T. Для идеального газа P=NkT/V, эта производная равна: V/T.
Переданное системе тепло при нагреве dT и изменении её объёма dV можно вычислить следующим образом: δQ = dU+PdV = CVdT + [(∂U∂V)T + P]dV = CVdT + CP−CV(∂V/∂T)PdV. Соответственно, для идеального газа: δQ=CVdT+kNTdV/V.
Энтропия
Ещё одна важная переменная состояния идеального газа называется энтропией: dS = δQT. Покажем, что для идеального газа dS действительно является полным дифференциалом. Подставляя уравнения U=NkT/(γ−1) и P=NkT/V в первое начало при постоянном числе частиц (N=const), получаем: dS = dU+PdVT = kNγ−1dTT+kNdVV = kNγ−1dln(TVγ−1). В переменных (P,V) этот же дифференциал равен: dS = kNγ−1dln(PVγ).
Энтропия - это аддитивная переменной состояния. Действительно, разделим мысленно объём газа на две части. Если газ получает некоторое тепло δQ, то оно распределяется между частями δQ=δQ1+δQ2 (T везде одинакова), пропорционально числу частиц и dS=dS1+dS2. Таким образом, для энтропии должно выполнятся общее свойство аддитивных величин: S(T,V,N)=N⋅s(T,V/N). Это свойство позволяет получит S с точностью до константы α, не зависящей от числа частиц (константа интегрирования dS зависит только от N): S(T,V,N) = kNγ−1lnT + kNlnVN + αN. В переменных (P,V) энтропия идеального газа имеет вид: S(P,V,N) = CVlnP + CPlnVN + α′N.
Говорят, что 1/T является интегрирующим множителем, который превращает малое приращение δQ в дифференциал. Первое начало термодинамики можно записать как дифференциал внутренней энергии, зависящей от S и V: dU=TdS−PdV, T=(∂U∂S)V,N, P=−(∂U∂V)S,N.
При помощи различных термодинамических потенциалов второе начало можно записывать в любой паре переменных состояния из множества {P,V,T,S}. Так, для энтальпии H=U+PV имеем dU=TdS+VdP. Другие потенциалы: свободная энергия Гельмгольца: F=U−TS и потенциал Гиббса: G = H−TS.
Равновесные процессы
Для описания любого равновесного процесса необходимо совместно использовать уравнения состояния и первое начало термодинамики. Рассмотрим два важных процесса.
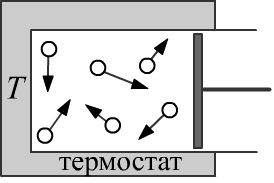 Изотермический равновесный процесс происходит при постоянной температуре T=const.
Изотермический равновесный процесс происходит при постоянной температуре T=const.
Для этого система должна находится в тепловом контакте с очень большим телом фиксированной (неизменной)
температуры T,
называемом термостатом. Так как для идеального газа U∼T,
то при изотермическом процессе внутренняя энергия не изменяется dU=0.
При расширении система получает теплоту, а при сжатии - отдаёт её:
Q = ∫δA = V2∫V1PdV P=ΘN/V = NΘlnV2V1.
Так как dS=δQ/T, при T=const изменение энтропии равно ΔS = Q/T.
Изотермический процесс имеет максимальный коэффициент полезного действия (КПД).
Это означает, что при расширении вся, полученная системой теплота Q идёт на совершение работы A: КПД=(A/Q). При сжатии системы, вся работа превращается в тепло, уходящее из системы в термостат.
Отметим, что изотерму T=const можно реализовать в статическом случае приводя в тепловой контакт сосуды с различным объёмом и равным числом частиц, получив зависимость P(V). Очевидно что, если термостат сравним по размеру с системой, то соответствующий равновесный процесс уже не будет изотермическим.
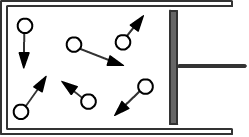 Адиабатический равновесный процесс происходит в изолированной
от теплового воздействия системе (внутри "термоса"). В этом случае δQ=0 и т.к. U=PV/(γ−1)
dU = −δA = −PdV ⇒ γdVV+dPP = 0 ⇒ PVγ = const.
Энтропия при адиабатическом процессе не изменяется S=const,
а температура при расширении газа уменьшается.
Уменьшение температуры (и внутренней энергии) происходит в результате совершения газом работы.
Это означает, что при отражении молекулы от "поддающегося" поршня
она теряет часть своей энергии. Если поршень отодвигать маленькими, но резкими
шажками, температура меняться не будет и процесс не будет адиабатическим
(как и вообще равновесным).
Адиабатический равновесный процесс происходит в изолированной
от теплового воздействия системе (внутри "термоса"). В этом случае δQ=0 и т.к. U=PV/(γ−1)
dU = −δA = −PdV ⇒ γdVV+dPP = 0 ⇒ PVγ = const.
Энтропия при адиабатическом процессе не изменяется S=const,
а температура при расширении газа уменьшается.
Уменьшение температуры (и внутренней энергии) происходит в результате совершения газом работы.
Это означает, что при отражении молекулы от "поддающегося" поршня
она теряет часть своей энергии. Если поршень отодвигать маленькими, но резкими
шажками, температура меняться не будет и процесс не будет адиабатическим
(как и вообще равновесным).
Аналогично анализируются изохорический [V=const, δA=0], изобарический [P=const, δA=d(PV)], политропный процесс [C=δQ/dT=const, Q=CΔT откуда PVn=const, где n=(C−CP)/(C−CV)] и другие процессы. Рассмотрим в качестве примера следующую задачу:
При движении теплопроницаемого поршня, температура в обоих частях объёма поддерживается одинаковой.
Так как вся система теплоизолирована, изменение её внутренней энергии связано с совершённой работой: A=ΔU=2N0(Θ−Θ0)/(γ−1), где N0 - число молекул в каждой части объёма (всего их 2N0), Θ=kT.
При сжатии второй части V0↦V2 выделяется тепло δQ2, которое через поршень переходит в первую часть: 0 = δQ1+δQ2 = dU1+P1dV1 + dU2+P2dV2 ⇒ dU = −(P1dV1+P2dV2). Подставив U=2N0Θ/(γ−1) и Pi=N0Θ/Vi, получим легко интегрируемое уравнение с решением: V1V2Θ2/(γ−1) = V20Θ2/(γ−1)0 ⇒ Θ = Θ0(43)(γ−1)/2 ⇒ A = 2P0V0γ−1[(43)(γ−1)/2−1].
Циклические процессы
В термодинамике и практических приложениях важную роль играют замкнутые циклы, состоящие из равновесных процессов. Изменяясь в этих процессах, система периодически возвращается в исходное состояние.
Напомним, что, если Q>0, то тепловая энергия получается системой, а при Q<0 - отдаётся наружу. Положительная работа δA = PdV означает, что её производит система (а не "мы"), а если A<0 - работа совершается над системой, т.е. "нами". Для замкнутого цикла ΔU=0 (возвращаемся в тоже состояние), поэтому A=Q, где: A = ∮PdV, = Q = ∮TdS.
Если обход контура равновесного процесса производится по часовой стрелке (см. стрелки на рисунках), то выполняемая системой работа A на плоскости (P,V) равна площади, окружаемой кривой цикла, а получаемая системой теплота Q - площади для этого же процесса на плоскости (T,S).

Действительно, интеграл от PdV по верхней кривой между точками (1−2) положителен и равен площади под этой кривой. Движение в обратную сторону (2−1) по нижней кривой приводит к "отрицательной площади" под этой кривой. Сумма этих площадей равна площади закрашенной области. Аналогично для плоскости (T,S).
Если направление контура меняется на противоположный, то меняются и знаки. Тепло система отдаёт Q<0, и чтобы такой цикл был возможен, необходимо затрачивать "внешнюю" работу: A=Q<0.
В силу того, что энтропия dS=δQ/T является переменной состояния, интеграл от неё по замкнутой кривой, как и для внутренней энергии, равен нулю: ∮δQT = 0. Это соотношение называют вторым началом термодинамики для равновесных процессов.
Цикл Карно
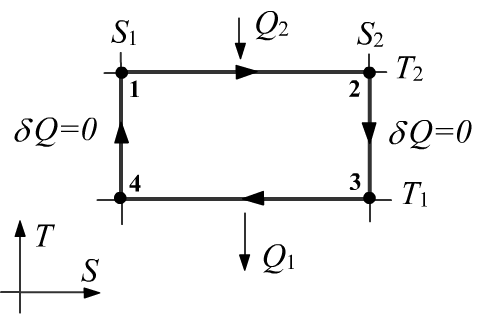 Рассмотрим в качестве примера цикл Карно, состоящий из
двух изотерм T1<T2 и двух
адиабат S1<S2.
На изотерме 1−2 система расширяясь,
получает тепло Q2>0 от термостата с температурой T2, а при сжатии на изотерме 3−4
отдаёт его Q1<0 термостату c температурой T1<T2.
Рассмотрим в качестве примера цикл Карно, состоящий из
двух изотерм T1<T2 и двух
адиабат S1<S2.
На изотерме 1−2 система расширяясь,
получает тепло Q2>0 от термостата с температурой T2, а при сжатии на изотерме 3−4
отдаёт его Q1<0 термостату c температурой T1<T2.
На плоскости (T,S) цикл Карно имеет форму прямоугольника. Так как δQ=TdS, на изотермах имеем Q2 = T2(S2−S1)>0 и Q1 = T1(S1−S2)<0, откуда сразу следует равенство Карно-Клаузиуса: Q1T1+Q2T2=0.
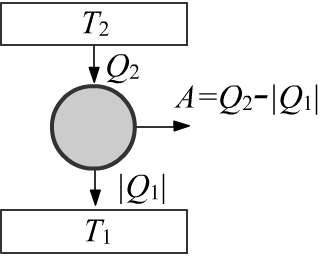 Коэффициентом полезного действия (КПД) цикла называют отношение выполненной работы
к полученному от более горячего термостата тепла:
η = AQ2 = Q1+Q2Q2 = 1−T1T2.
Так как T1<T2, КПД всегда меньше единицы. Тепловая машина, работающая
по циклу Карно, производит работу благодаря градиенту температур в термостатах.
Коэффициентом полезного действия (КПД) цикла называют отношение выполненной работы
к полученному от более горячего термостата тепла:
η = AQ2 = Q1+Q2Q2 = 1−T1T2.
Так как T1<T2, КПД всегда меньше единицы. Тепловая машина, работающая
по циклу Карно, производит работу благодаря градиенту температур в термостатах.
При наличии только одного термостата циклически производить работу нельзя.
Чуть более сложно выглядит анализ цикла Карно в переменных (P,V). Для получаемого Q2 и отдаваемого Q1 тепла можно воспользоваться результатом анализа изотермического процесса:
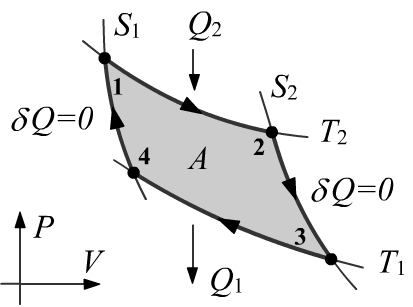 Q2 = kNT2lnV2V1, Q1 = kNT1lnV4V3.
Q2 = kNT2lnV2V1, Q1 = kNT1lnV4V3.
На адиабатах PVγ = TVγ−1 = const, откуда T1Vγ−13=T2Vγ−12 и T1Vγ−14=T2Vγ−11, или V2V1 = V3V4. Отсюда уже несложно получить связь Q1/T1+Q2/T2=0. Замечательным является то, что в это соотношение не входит параметр γ, т.е. оно должно выполнятся любого идеального газа. Более того, природа используемой в цикле системы (рабочего тела) вообще роли не играет. Именно это наблюдение исторически привело к понятию энтропии.
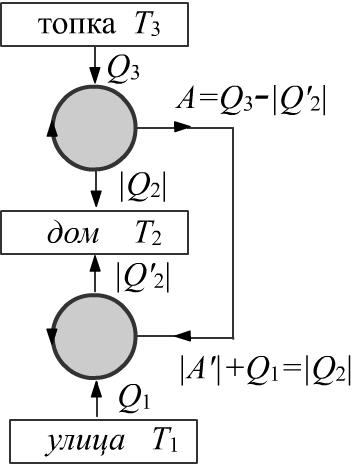 Тепловая машина производит работу A. Холодильная машина эту работу потребляет:
A=Q3+Q2>0, A′ = Q1+Q′2 = −A<0
Откуда Q1+Q′2+Q2+Q3 = 0. Кроме этого: Q3/T3+Q2/T2 = Q1/T1+Q′2/T2=0.
Тепло, приходящее в дом, равно Qget = |Q2|+|Q′2| = Q1+Q3. В результате:
QgetQ3 = T−11−T−13T−11−T−12.
Пусть в градусах Цельсия t1=0°, t2=20° и t3=100°. Тогда Qget/Q3=3.9.
Тепловая машина производит работу A. Холодильная машина эту работу потребляет:
A=Q3+Q2>0, A′ = Q1+Q′2 = −A<0
Откуда Q1+Q′2+Q2+Q3 = 0. Кроме этого: Q3/T3+Q2/T2 = Q1/T1+Q′2/T2=0.
Тепло, приходящее в дом, равно Qget = |Q2|+|Q′2| = Q1+Q3. В результате:
QgetQ3 = T−11−T−13T−11−T−12.
Пусть в градусах Цельсия t1=0°, t2=20° и t3=100°. Тогда Qget/Q3=3.9.
Второе начало для равновесных процессов
Равновесные состояния адиабатического процесса δQ=0 для идеального газа на плоскости (P,V) находятся на кривой PVγ=const. Поэтому из данного состояния при помощи только одной адиабаты нельзя попасть в произвольное состояние (в произвольную точку на (P,V) плоскости). Это утверждение, называемое принципом адиабатической недостижимости Каратеодори, справедливо для любой термодинамической системы.
Следствием "принципа недостижимости" является то, что изотермы и адиабаты на плоскости (P,V) могут пересекаться не более, чем в одной точке. Это несложно доказать, пользуясь вторым началом термодинамики, в форме запрета вечного двигателя второго рода:
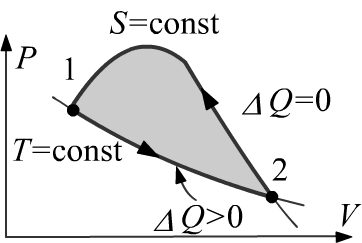 Действительно, пусть изотермический процесс соединяет два состояния
(точки 1 и 2).
Действительно, пусть изотермический процесс соединяет два состояния
(точки 1 и 2).
В этом процессе система получает от термостата
тепло ΔQ = (U2−U1)+ΔA>0.
Допустим, что возможен обратный (из точки 2 в точку 1)
адиабатический процесс для которого ΔQ=0=(U1−U2)+Δ˜A.
Складывая эти два соотношения, получаем ΔA+Δ˜A>0.
Это означает, что в таком замкнутом цикле система производит работу,
что противоречит второму началу.
Каждая изотерма соответствует определённой температуре T,
которая её "нумерует". Эти изотермы не пересекаются (они соответствуют различным термостатам)
и непрерывно заполняют плоскость (P,V).
Точно также принцип адиабатической недостижимости означает,
что адиабаты непересекаясь, заполняют всю плоскость состояний.
Соответственно, можно ввести переменную состояния, которая нумерует адиабаты.
Эту переменную и называют энтропией.
Аксиоматическое определение энтропии
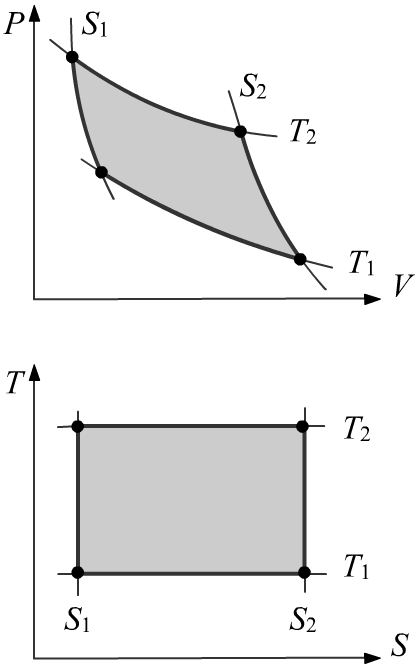 Существует определённый произвол в нумерации изотерм и адиабат.
Он устраняется, если выполнить нумерацию таким образом, чтобы при переходе от переменных (P,V) к переменным
(T,S)
бесконечно малый объём оставался неизменным. Для этого якобиан
должен быть равен единице:
dPdV ↔ dTdS ⇒ ∂(T,S)∂(P,V) = |∂T∂P∂T∂V∂S∂P∂S∂V| = 1.
Действительно, например, для идеального газа:
dS=CV[dPP+γdVV] ⇒ ∂S∂P = CVP, ∂S∂V = γCVV.
Подставляя значения частных производных ∂S/∂P и ∂S/∂T
в якобиан, получаем 1.
Существует определённый произвол в нумерации изотерм и адиабат.
Он устраняется, если выполнить нумерацию таким образом, чтобы при переходе от переменных (P,V) к переменным
(T,S)
бесконечно малый объём оставался неизменным. Для этого якобиан
должен быть равен единице:
dPdV ↔ dTdS ⇒ ∂(T,S)∂(P,V) = |∂T∂P∂T∂V∂S∂P∂S∂V| = 1.
Действительно, например, для идеального газа:
dS=CV[dPP+γdVV] ⇒ ∂S∂P = CVP, ∂S∂V = γCVV.
Подставляя значения частных производных ∂S/∂P и ∂S/∂T
в якобиан, получаем 1.
Для произвольной системы с уравнением состояния T=T(P,V/N) энтропию можно определить как переменную состояния являющейся решением уравнения (единичный якобиан P,V↦T,S): ∂T∂P∂S∂V − ∂T∂V∂S∂P = 1.