Теория вещества: 3. Неравновесные процессы

---

Введение

---

Необратимое расширение

Чтобы газ в сосуде с поршнем находился в термодинамическом равновесии, к поршню необходимо всё время прикладывать силу, компенсируя давление газа. При равновесном процессе поршень медленно сдвигают, продолжая прикладывать к нему силу, чтобы после сдвига он оставался неподвижным (и установилось термодинамическое равновесие). Поэтому при увеличении объёма газ совершает работу, что понижает его внутреннию энергию и температуру (в адиабатическом случае).

Рассмотрим, что произойдёт, если поршень начать сдвигать быстро.
Возле него неизбежно возникнет зона разряжения газа и давление на поршень будет меньше, чем при медленном равновесном процессе.
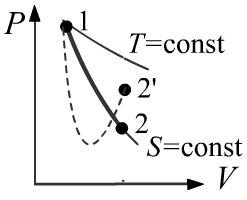
В результате, такой процесс будет не равновесным. Тем не менее нарисуем диаграмму на плоскости $(P,V)$, понимая под $P$ не единое давление во всём объёме (которого уже нет), а давление газа непосредственно на поршень.
Это давление (справа пунктирная линия), благодаря области разряжения, будет отставать от давления на равновесной адиабатической кривой (сплошная линия $S=\text{const}$). Соответственно работа газа $A'$ по расширению в неравном случае будет меньше, чем работа $A$ в равновесном. Внутренняя энергия $dU=-P\,dV$ при не равновесном процессе уменьшится меньше и температура будет выше. После остановки поршня, давление на него (как и температура) вырастет. При обратном движении (неравновесное сжатие после установления равновесия) давление будет опережать равновесную кривую и температура снова повысится. Таким образом мы имеем нециклический процесс.

Если сосуд погружен в термостат, то подобный процесс может быть циклическим (если ожидать установления равновесного состояния), но по-прежнему будет неравновесным.

---

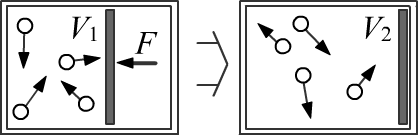Пусть есть теплоизолированный цилиндрический сосуд, разделённый на две части лёгким поршнем. В одной части объёмом $V_1$ находится газ под давлением $P_1$ и с температурой $T_1$. Во второй части объёмом $V_2-V_1$ ничего нет. Предположим, что система пришла в равновесие, после чего поршень перестали удерживать. Под давлением газа он начнёт двигаться вправо, пока не достигнет стенки сосуда. Эквивалентно, поршень можно просто убрать.

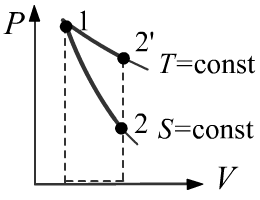Так как работа не совершалась (нет силы), поршень лёгкий (нет кинетической энергии) и сосуд теплоизолирован (нет потока тепла), внутренние энергии начального и конечного равновесных состояний одинаковы. Следовательно, в этом случае температура газа не изменится: $T_1=T_2$. Адиабатический процесс не может быть одновременно изотермическим, что также свидетельствует о неравновесности подобного расширения.

Энтропия - это аддитивная переменная состояния и в данном равновесном состоянии содержится определённое количество энтропии (подобно внутренней энергии $U$ или числу частиц $N$).
Поэтому определим изменении энтропии в неравновесном процессе как разность энтропий конечного и начального равновесных состояний. Чтобы найти подобную разность можно взять любой равновесный процесс, который эти состояния мог бы связать. Для переменной состояния выбор равновесного процесса роли не играет.

При постоянстве температур $T_1=T_2$, в качестве такого процесса лучше подходит изотермический, для которого: $$(\Delta S)_{T,N} ~=~ k\,N\,\ln\frac{V_2}{V_1}~~\gt ~ 0.$$

Таким образом, можно сказать, что в неравновесном процессе свободного движения поршня энтропия выросла (энтропия нового равновесного состояния больше, чем у исходного). Понятно, что этот процесс необратимый (поршень сам не вернётся в начальное положение).

---

Выравнивание температур

Во втором примере рассмотрим тепловой контакт двух сосудов, с температурами $T_1$ и $T_2$. Опыт (и рассуждения о выравнивании кинетических энергий) говорит от том, что через некоторое время температуры в сосудах сравняются на некотором значении $T$.

Пусть для определённости $T_1\lt T_2$. Так как система замкнута, суммарная внутренняя энергия не изменяется: $\Delta (U_1+U_2) = 0$. Начальное и конечное состояния равновесные, поэтому можно подставить $\Delta U_1=C_{V1}\,(T-T_1)$ и $\Delta U_2=C_{V2}\,(T_2-T)$. Отсюда следует, что $$T=(C_{V1}\, T_1+C_{V2}\,T_2)/(C_{V1}+C_{V2}).$$ Напомним, что теплоёмкость $C_V$ пропорциональна массе тела (или числу молекул). Если одно тело много больше второго: $C_{V2} \gg C_{V1}$, то температура большего тела изменится мало: $T\approx T_2$. Для одинаковых тел $T=(T_1+T_2)/2$.

Процесс выравнивания температур необратим (температуры сами не вернутся к начальным значениям). Соответственно, он не может быть и равновесным процессом. Тем не менее, как и в предыдущем примере, вычислим изменение энтропии при помощи равновесного процесса, связывающего начальное и конечное состояния.

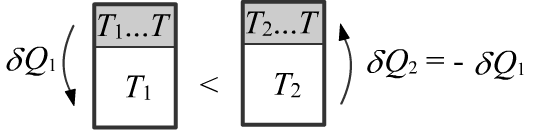Сосуды имеют тепловой контакт только друг с другом, поэтому $\delta (Q_1+ Q_2) = 0$ (тепло из более горячего переходит к более холодному). Эквивалентно, можно считать, сосуды контактируют не друг с другом, а с внешними термостатами. В первом термостате температура медленно повышается с $T_1$ до $T$, а во втором снижается с $T_2$ до $T$.

Пусть $V_i=\text{const}$ (изохорические процессы). Тогда $\delta A = 0$ и $\delta Q = dU = C_V\,dT$. Для равновесной температуры $T$, полученной выше, $\Delta Q_1+\Delta Q_2=0$. Изменение равновесной энтропии $dS=\delta Q/T$, при переходе от температуры $T_1$ к $T$ равно:

$$(\Delta S)_{V,N} ~=~ C_V\,\ln\frac{T}{T_1}.$$ Соответственно, складывая эти изменения для каждого сосуда, получаем: $$\Delta S ~=~ (S'_1-S_1)+(S'_2-S_2) ~=~ C_{V1}\,\ln\frac{T}{T_1}+C_{V2}\,\ln\frac{T}{T_2}~\gt~ 0.$$ Например, для равных сосудов $T=(T_1+T_2)/2$, имеем $\Delta S~=~C_V\,\ln ((T_1+T_2)^2/2 T_1 T_2)\gt 0.$

---

Смешивание газов

Рассмотрим сосуд объёма $V$, в котором при температуре $T$ в термодинамическом равновесии находится несколько разновидностей молекул числом $N_1,\,N_2,...$ Энтропия такой смеси равна сумме энтропий каждой компоненты. Одно из возможных мотиваций правильности этого утверждения принадлежит Гиббсу. Как суммарная внутренняя энергия равна сумме энергий каждой компоненты $U_1+U_2+...$, так и давление $P$ равно сумме парциальных давлений $P_1+P_2+...$ (закон Дальтона). Поэтому можно написать: $$dS = \frac{dU+P\,dV}{T} = \sum_i \frac{dU_i+P_i\,dV}{T} = \sum_i dS_i.$$ Повторяя для каждой компоненты проделанный ранее вывод, получаем: $$S ~=~ \sum_i \Bigr[\frac{k\,N_i}{\gamma_i-1}\,\ln T ~+~ k\,N_i\,\ln\frac{V}{N_i} ~+~\alpha_i\,N_i\Bigr].$$

---

Пусть есть два одинаковых сосуда объёма $V$, разделённых перегородкой. В одном сосуде находится $N_1$ молекул одного вида, а во втором $N_2$ - другого. Энтропия всей системы равна сумме энтропий каждого сосуда. После того как перегородку убирают газы смешиваются, занимая объём $2\,V$. Так как система предполагается адиабатически изолированной и работа не совершается, внутренняя энергия и температура системы останутся неизменными. Поэтому изменение энтропии будет равно: $$(\Delta S)_{T,N} = k\,\Bigr[N_1\,\ln\frac{2V}{N_1}+N_2\,\ln\frac{2V}{N_2}\Bigr] - k\,\Bigr[N_1\,\ln\frac{V}{N_1}+N_2\,\ln\frac{V}{N_2}\Bigr] = k\,(N_1+N_2)\,\ln 2.$$ В эту формулу не входят параметры характеризующие компоненты смеси (например $\gamma_i$). Поэтому она должна быть справедлива и для сколь угодно "похожих" молекул (а пределе для одинаковых). Однако, если $N_1=N_2$, то устранение перегородки разделяющей один и тот же газ не должно изменить энтропию системы. Это рассуждение называется парадоксом Гиббса.

---

Второе начало термодинамики

В рассмотренных выше примерах не утверждалось, что энтропия растёт в течении неравновесного процесса. Строго говоря она, как температура или давление, в таком процессе может быть и неопределённой (нет единого числа, одинакового во всех частях системы). Однако, новое равновесное состояние в которое переходит система при неравновесном процессе, имеет большую энтропию, чем исходное: $\Delta S=S_2-S_1 \gt 0$.

---

---