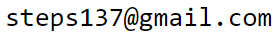Теория вещества: 1. Идеальный газ
Введение
Модель идеального газа - это простейшая статистическая модель, неплохо описывающая физику реальных газов. Рассмотрим сосуд объёмом V в котором движутся небольшие шарики массы m. При движении они упруго сталкиваются друг с другом (подобно бильярдным шарам, но без вращения) и не теряя энергии, отражаются от стенок сосуда. Далее эти шарики будут называться одноатомными молекулами.
В реальных газах молекул очень много. В результате столкновений, они быстро "забывают" начальные условия (положение и скорость) и их движение становится случайным. В частности, независимо от начальных условий, концентрация частиц в различных частях объёма со временем оказывается примерно одинаковой, а средняя скорость (по всем частицам) равной нулю. Такое состояние называется равновесным.
Давление и работа
 Пусть сосуд имеет форму цилиндра, в основании которого находится поршень площади S.
Молекулы постоянно налетают на поршень, "толкая его".
Поэтому для удержания поршня в неподвижном состоянии к нему необходимо прикладывать
некоторую силу −F, которая компенсирует такую же силу F (с противоположным направлением) со стороны газа
(третий закон Ньютона).
На рисунке справа источником внешней силы −F является сжатая пружина.
Когда система приходит в равновесие, давление со стороны газа уравновешивается силой со стороны пружины.
Пусть сосуд имеет форму цилиндра, в основании которого находится поршень площади S.
Молекулы постоянно налетают на поршень, "толкая его".
Поэтому для удержания поршня в неподвижном состоянии к нему необходимо прикладывать
некоторую силу −F, которая компенсирует такую же силу F (с противоположным направлением) со стороны газа
(третий закон Ньютона).
На рисунке справа источником внешней силы −F является сжатая пружина.
Когда система приходит в равновесие, давление со стороны газа уравновешивается силой со стороны пружины.
По определению, давление равно отношению силы F со стороны газа,
приложенной к поршню площади S:
P=FS.
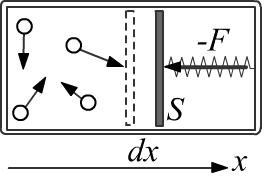
 Давление газа является его важной характеристикой,
описывающей (наравне с объёмом V) равновесное состояние газа.
Давление - это положительная, скалярная величина.
Компенсирующая его нормальная (перпендикулярная поверхности) сила одинакова при любых ориентациях поверхности
и в любых точках объёма (см. второй рисунок).
Давление газа является его важной характеристикой,
описывающей (наравне с объёмом V) равновесное состояние газа.
Давление - это положительная, скалярная величина.
Компенсирующая его нормальная (перпендикулярная поверхности) сила одинакова при любых ориентациях поверхности
и в любых точках объёма (см. второй рисунок).
Если газ начать нагревать, скорость молекул увеличится. Поэтому увеличатся частота и сила ударов молекул о поршень. Соответственно, вырастет и давление газа. Это приведёт к тому, что поршень начнёт сдвигаться вправо, ещё сильнее сжимая пружину, пока не достигнет нового равновесного состояния. Увеличивая свой объём dV=Sdx, газ совершает работу, равную: δA=Fdx=Fxdx=FxSSdx=PdV. Так как δA - это работа совершаемая газом, то сила F направлена вдоль оси x (противоположно компенсирующей силе пружины). Когда объём увеличивается (dV>0), то газ совершает работу: δA>0. При уменьшении объёма (dV<0) работа газа отрицательна: δA<0. Это означает, что для сжатия газа необходимо затратить работу со стороны внешних сил.
 ☝ Подчернём, что работа совершается газом только, если молекулы отражаются от поршня неупруго,
теряя при столкновении часть своего импульса.
Когда поршень резко выдвигают, молекулы не теряют своей энергии
и газ работу не совершает.
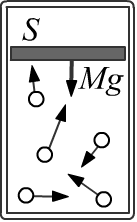
В качестве примера произведенной работы, рассмотрим цилиндрический сосуд,
в верхнем основании которого находится подвижный тяжёлый поршень массы M и площади S.
В равновесии сила давления газа PS уравновешивается весом поршня Mg (на поршень сверху ничего не давит).
Газ можно начать нагревать, в результате чего поршень начнёт подниматься.
Вторая возможность - медленно уменьшать массу поршня, что также приведёт к его поднятию.
В обоих этих случаях газ совершает работу.
☝ Подчернём, что работа совершается газом только, если молекулы отражаются от поршня неупруго,
теряя при столкновении часть своего импульса.
Когда поршень резко выдвигают, молекулы не теряют своей энергии
и газ работу не совершает.
В качестве примера произведенной работы, рассмотрим цилиндрический сосуд,
в верхнем основании которого находится подвижный тяжёлый поршень массы M и площади S.
В равновесии сила давления газа PS уравновешивается весом поршня Mg (на поршень сверху ничего не давит).
Газ можно начать нагревать, в результате чего поршень начнёт подниматься.
Вторая возможность - медленно уменьшать массу поршня, что также приведёт к его поднятию.
В обоих этих случаях газ совершает работу.
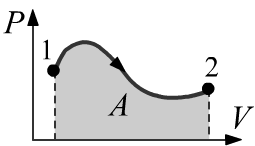 При изменении объёма газа может меняться его давление.
Подобная зависимость P=P(V) изображается на декартовой
плоскости (P,V) с координатными осями на которых отложено давление
и объём. Работа, совершаемая газом, равна площади под кривой P(V):
A=2∫1PdV.
Эта площадь положительна при расширении и отрицательна при сжатии.
В последнем случае стрелка на контуре будет направлена в обратную сторону (интегрирование от 2 к 1).
При изменении объёма газа может меняться его давление.
Подобная зависимость P=P(V) изображается на декартовой
плоскости (P,V) с координатными осями на которых отложено давление
и объём. Работа, совершаемая газом, равна площади под кривой P(V):
A=2∫1PdV.
Эта площадь положительна при расширении и отрицательна при сжатии.
В последнем случае стрелка на контуре будет направлена в обратную сторону (интегрирование от 2 к 1).
Давление идеального газа
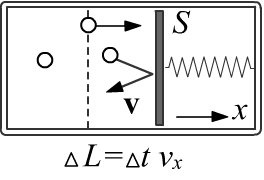 Найдём давление, оказываемое идеальным газом на неподвижный поршень (или стенку сосуда).
Для этого рядом с поршнем выделим тонкий слой газа ширины ΔL,
в котором можно пренебречь столкновениями молекул друг с другом (но их там должно быть по-прежнему много).
Если S - это площадь поршня, то объём слоя равен V=SΔL.
Найдём давление, оказываемое идеальным газом на неподвижный поршень (или стенку сосуда).
Для этого рядом с поршнем выделим тонкий слой газа ширины ΔL,
в котором можно пренебречь столкновениями молекул друг с другом (но их там должно быть по-прежнему много).
Если S - это площадь поршня, то объём слоя равен V=SΔL.
Рассмотрим Nv молекул, которые имеют примерно одинаковую компоненту скорости vx и движутся в направлении поршня (vx>0). За время Δt=ΔL/vx эти молекулы из слоя шириной ΔL, успеют столкнутся с поршнем (последними - молекулы, находящиеся на границе слоя). После упругого столкновения (поршень неподвижен), компонента импульса px молекул меняет знак и полное изменение их импульса, переданное поршню, равно Δpx=2px. Поэтому суммарное давление со стороны этих молекул на поршень равно: P = FxS = NvΔpxΔt1S = Nv2pxSΔt = 2NvVpxvx.
Молекулы газа движутся с различными скоростями v={vx,vy,vz}, в различных направлениях.
В результате столкновений молекул друг с другом, их скорости постоянно изменяются, становясь случайными величинами.
Пусть f(vx) - это плотность распределения вероятностей для скоростей vx.
Оно нормировано на единицу (интеграл от него по dvx равен 1).
Естественно считать это распределение симметричным.
Число молекул Nv, имеющих компоненту скорости vx с небольшим разбросом dvx, по определению,
равно Nv = Nf(vx)dvx, где N - общее число молекул (с любыми скоростями):
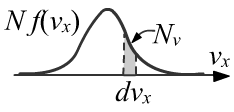 ∞∫−∞f(vx)dvx=1, f(−vx)=f(vx).
∞∫−∞f(vx)dvx=1, f(−vx)=f(vx).
Полное давление равно сумме давлений со стороны молекул, движущихся со всеми возможными скоростями vx в направлении поршня (vx>0): P = 2NV∞∫0pxvxf(vx)dvx = NV∞∫−∞pxvxf(vx)dvx=NV⟨pxvx⟩, где учтена симметричность распределения и угловыми скобками обозначено среднее значение (интеграл). Так как направления в пространстве равноправны: ⟨pv⟩=⟨pxvx+pyvy+pzvz⟩=3⟨pxvx⟩, окончательно имеем: P = n⟨pv⟩3, n=NV. Отношение числа молекул N к объёму n=N/V называется концентрацией молекул (число в единице объёма). Обратная величина v=V/N, называемая удельным объёмом, - это часть объёма сосуда, приходящаяся на одну молекулу. Усреднение по всем направлениям скорости производится при помощи тройного интеграла с весами равными распределению каждой компоненты скорости: f(vx)f(vy)f(vz)dvxdvydvz.
Для нерелятивистского газа импульс молекул равен p=mv, поэтому полученное соотношение можно переписать следующим образом: PV = 23N⟨mv22⟩, где под знаком среднего находится кинетическая энергия поступательного движения молекулы.
Выравнивание кинетических энергий
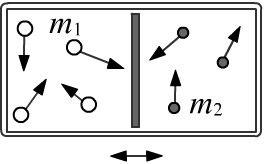 Пусть сосуд разделён на две части лёким подвижным поршнем.
В одной части, объёмом V1, находится N1 молекул с массами m1,
а во второй части V2 есть N2 молекул массами m2.
Так как поршень подвижен, в равновесии давление в обоих частях должно быть одинаковым.
Совпадают также и средние значения кинетических энергий молекул:
⟨m1v212⟩ = ⟨m2v222⟩.
Пусть сосуд разделён на две части лёким подвижным поршнем.
В одной части, объёмом V1, находится N1 молекул с массами m1,
а во второй части V2 есть N2 молекул массами m2.
Так как поршень подвижен, в равновесии давление в обоих частях должно быть одинаковым.
Совпадают также и средние значения кинетических энергий молекул:
⟨m1v212⟩ = ⟨m2v222⟩.
Действительно, молекула из одной половины сосуда, налетая на поршень, передаёт ему часть своего импульса (поршень подвижен). Поршень начинает двигаться навстречу молекулам из другой части сосуда. Сталкиваясь с ними, он передаёт им этот импульс. Его "подёргивания" туда-сюда приводят к выравниванию средней кинетической энергии молекул слева и справа от поршня.
Отметим, что при столкновении молекулы с поршнем, она передаёт ему свой импульс, но не может передать момент вращения или внутреннюю колебательную энергию. Поэтому в результате выравниваются именно кинетические энергии поступательного движения молекул.
 В качестве второго примера рассмотрим газовую смесь, состоящую из молекул двух типов с массами m1 и m2.
Пусть две такие молекулы движутся со скоростями v1 и v2.
В равновесном состоянии скорости молекул имеют произвольные направления и нескоррелированы друг с другом.
Это означает, что совместная плотность распределения вероятностей равна произведению распределений для
каждой молекулы: f(v1,v2)=f1(v1)f2(v2),
поэтому: ⟨v1v2⟩=⟨v1⟩⟨v2⟩=0:
⟨v1v2⟩=∫f(v1,v2)v1v2d3v1d3v2 = ∫f1(v1)v1d3v1⋅∫f1(v2)v2d3v2 = ⟨v1⟩⟨v2⟩.
В качестве второго примера рассмотрим газовую смесь, состоящую из молекул двух типов с массами m1 и m2.
Пусть две такие молекулы движутся со скоростями v1 и v2.
В равновесном состоянии скорости молекул имеют произвольные направления и нескоррелированы друг с другом.
Это означает, что совместная плотность распределения вероятностей равна произведению распределений для
каждой молекулы: f(v1,v2)=f1(v1)f2(v2),
поэтому: ⟨v1v2⟩=⟨v1⟩⟨v2⟩=0:
⟨v1v2⟩=∫f(v1,v2)v1v2d3v1d3v2 = ∫f1(v1)v1d3v1⋅∫f1(v2)v2d3v2 = ⟨v1⟩⟨v2⟩.
В силу закона сохранения импульса, суммарный импульс m1v1+m2v2 молекул при столкновении не изменяется, а меняется относительная скорость v2−v1. В системе отсчёта центра масс (где суммарный импульс равен нулю), распределение вектора относительной скорости должно быть изотропным (нет выделенных направлений). Поэтому, суммарный импульс и относительная скорость также должны быть нескоррелированными: 0=⟨(v2−v1)(m1v1+m2v2)⟩=⟨m2v22⟩ − ⟨m1v21⟩, откуда следует равенство средних кинетических энергий молекул в смеси двух газов.
В общем случае, даже если молекулы вращаются или обладают внутренними колебаниями, в результате столкновений друг с другом или перегородками, выравниваются именно их средние кинетические энергии поступательного движения.
Температура
Определим температуру T, как величину,
пропорциональную средней кинетической энергии молекулы:
⟨mv22⟩ = 32kT,
где k=1.380649⋅10−23Дж/K - постоянная Больцмана. Она "пересчитывает"
градусы температуры, измеряемую в кельвинах (К) в энергию (джоули, Дж).
Если t - это температура в градусах Цельсия (°C), то: T = 273.15 + t.
Часто удобно для краткости использовать "энергетическую" температуру Θ=kT, измеряемую в джоулях.
Связь давления, объёма и температуры идеального газа теперь записывается в виде уравнения состояния: PV = NkT или P=nΘ.
Идеальный газ можно рассматривать как термометрическое тело. Выравнивание его температуры (средней поступательной кинетической энергии) с любым другим газом (в равновесии) по определению является температурой этого газа. При этом постулируется транзитивность равновесности (если системы A и B независимо находятся в тепловом равновесии с системой C, то они находятся в равновесии и друг с другом). Например, пусть есть две системы, состоящие из различных идеальных газов и находящихся в тепловом контакте. По определению считается, что в равновесии их температуры одинаковы: Θ = P1n1 = P2n2. Если дополнительно между ними находится подвижная перегородка, то совпадают их давления P1=P2 и, следовательно, концентрации числа частиц n1=n2.
Парциальным давлением называется давление данной компоненты газовой смеси, которое она создаёт при том же объеме и температуре в отсутствии других компонент смеси. Так как PV = (N1+N2+...)Θ, то давление смеси идеальных газов равно сумме парциальных давлений компонент. Это называется законом Дальтона.
Внутренняя энергия
Энергия "точечной" молекулы, движущейся без вращения, равна mv2/2. Определим внутреннию энергию газа одноатомных молекул как суммарное значение средних энергий N молекул такого газа: U = N⟨mv22⟩ = N32kT = N32Θ.
В общем случае связь внутренней
энергии и температуры зависит от "устройства" молекул. Поэтому её
удобно записать в следующем виде:
U = NΘγ−1 = PVγ−1,
где для одноатомного нерелятивистского идеального газа γ=5/3. В случае сложных молекул
или при релятивистских скоростях параметр γ может отличаться от значения 5/3, но он всегда больше единицы.
Например, кванты излучения с энергией E, движутся со скоростью света |v|=c. Для них справедливо соотношение pv=E, поэтому PV = N⟨pv⟩/3 = NE/3=U/3, т.е. γ=4/3.
Как изменилась при этом внутренняя энергия воздуха?
Объём и давление в комнате неизменны: PV=kNT=const. При нагревании уменьшается концентрация молекул воздуха n=N/V. Внутренняя энергия воздуха в комнате не меняется: U=kNT/(γ−1)=const.
Степени свободы молекул
Выше, при вычислении давления газа использовалась модель "точечных", не вращающихся молекул.
В более общем случае, введенный параметр γ связан с числом степеней свободы f молекулы:
γ−1 = 2f.
Для одноатомного газа ("точечные" шарики с тремя координатами) есть три степени свободы: f=3, γ=5/3.
Если молекулы двухатомного газа подобны тонкой жёсткой
гантельке, то f=5 (три координаты центра масс и два угла, т.к. вращение вокруг оси не вносит вклада в энергию).
Для жёсткой трёхатомной молекулы f=6.
Колебательния молекул (при высоких температурах) также увеличивают f, а, следовательно, уменьшают γ.
Например, если одноатомная молекула - это вращающиеся "шарики", то удельная внутренняя энергия (в расчёте на одну молекулу) такого газа равна сумме энергий поступательного движения и вращения: UN = ⟨mv22⟩ + ⟨Iw22⟩, где I - момент вращения, а w - угловая скорость. Можно показать, что средние значения энергии движения и вращения совпадают, поэтому: UN = 2⟨mv22⟩ = 62kT, откуда f=6 и γ=4/3. В общем случае каждая степень свободы даёт вклад в удельную внутреннею энергию, равную kT/2. UN = fkT2 = Θγ−1. Это утверждение называется теоремой о равнораспределении. Впрочем, на практике параметр γ для конкретного газа обычно не вычисляется, а определяется из эксперимента. Это же относится к эмпирическим модификациям простейшего уравнения состояния P=nΘ.
Единицы измерений
Молекул в макроскопических системах очень много, поэтому
их количество принято измерять в молях.
Один моль содержит NA=6.022 140 76⋅1023 штук молекул (число Авогадро - это точное целое число).
Произведение NA
на постоянную Больцмана k=1.380 649⋅10−23Дж/K (точно)
называют газовой постоянной:
R=kNA=8.314 462 618 153 24Дж/моль⋅K.
Если число молекул N измеряют в молях, а не в штуках, то уравнение состояния идеального
газа принимает вид:
PV = NRT.
Молекулярная масса - это масса одной молекулы. Её измеряют в единицах массы mu=1.660 565⋅10−27кг, равной одной двенадцатой массы атома углерода 612C, где верхний индекс у элемента - это число протонов (заряд ядра), нижний - общее количество протонов и нейтронов Удобно помнить, простое соотношение: muNA≈1г/моль.
Молярная масса - это масса одного моля вещества. Молярная масса двухатомного водорода 11H2 примерно равна 2г/моль, у воды H2(816O) - это ≈ (2+16)г/моль = 18г/моль. Воздух, которым мы дышим, является смесью газов: 0.76⋅714N2+0.23⋅816O2+0.01⋅1840Ar+... (по массе).
В системе Си давление измеряется в паскалях: Па=Н/м2, а объём иногда измеряют в литрах: 1л=10−3м3 (кубик со стороной 10см). Тепловую энергию измеряют в калориях: 1кал = 4.1868Дж. Нормальным давлением и температурой принято считать: P = 1атм = 1.01325⋅105Па и T = 273.15K. В этих условиях в одном кубическом метре содержится 44.6 моля молекул газа: 1.01⋅105⋅1/(8.31⋅273.15).
Молекулы имеют размеры порядка ангстрема 1Å = 10−8см = 10−10м. Например, диаметр атома водорода 2rB=1.06Å. Разброс диаметров молекул простых газов невелик: d(H2) = 2.7Å, d(O2) = 3.6Å, d(H2O) = 2.9Å, d(N2) = 3.7Å. Расстояние между молекулами газа при нормальных условиях порядка 30Å = (1м3/44.5⋅6.021023)1/3 (в 10 раз больше их типных размеров). В жидкости и твёрдых телах молекулы "упакованы" достаточно плотно. Например плотность воды 103кг/м3, поэтому при молярной массе 18г/моль, в кубическом метре находится 55⋅103NA молекул. Типичное расстояние между ними равно 3.1Å = (1м3/55⋅103⋅6.021023)1/3. Это приводит к тому, что вода оказывается практически несжимаемой.
Газ в поле тяжести
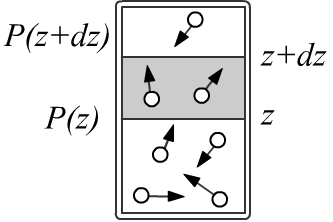 Пусть идеальный газ находится в вертикальном цилиндре с площадью основания S,
расположенном в поле силы тяжести.
Будем считать, что декартова ось z направлена вверх и нижнее основание цилиндра имеет координату z=0.
Рассмотрим слой газа, между координатами z и z+dz с концентрацией молекул n(z).
Если масса молекулы равна m, то масса всего слоя равна mn(z)Sdz.
На него действует сила F=−mg (ускорение свободного падения направлено вниз).
Что-бы слой был в покое, эта сила должна скомпенсироваться разностью давлений
на верхнюю и нижнюю границу слоя (можно мысленно представить там лёгкие перегородки):
F = [P(z+dz)−P(z)]S = −mgn(z)Sdz ⇒ dPdz = −mgn(z).
Будем считать, что температура во всём цилиндре одинакова и равна Θ = kT.
Учитывая уравнение состояния P = nΘ, имеем:
dnn = −mgΘdz ⇒ n(z) = n(0)e−mgz/Θ = n(0)e−U(z)/Θ,
где U(z) - потенциальная энергия молекулы.
Эту барометрическую формулу в 1821 г. получил Пьер Лаплас. Умножим числитель и знаменатель под экспонентой
на число Авагадро NA, введя μ=mNA - молярную массу и газовую постоянную R=kNA.
Тогда для воздуха (азот μ=28г/моль) при T=273, имеем
n(z) = n(0)exp(−μgzRT) = n(0)exp(−2⋅14⋅10−3кг/моль⋅9.88.31⋅273z)=n(0)e−z/10км.
Заметим, что концентрация молекул падает тем быстрее, чем больше молярная масса.
Так как у кислорода 816O2 она несколько больше, чем у азота 714N2,
с высотой, в воздухе процентное содержание кислорода уменьшается.
Пусть идеальный газ находится в вертикальном цилиндре с площадью основания S,
расположенном в поле силы тяжести.
Будем считать, что декартова ось z направлена вверх и нижнее основание цилиндра имеет координату z=0.
Рассмотрим слой газа, между координатами z и z+dz с концентрацией молекул n(z).
Если масса молекулы равна m, то масса всего слоя равна mn(z)Sdz.
На него действует сила F=−mg (ускорение свободного падения направлено вниз).
Что-бы слой был в покое, эта сила должна скомпенсироваться разностью давлений
на верхнюю и нижнюю границу слоя (можно мысленно представить там лёгкие перегородки):
F = [P(z+dz)−P(z)]S = −mgn(z)Sdz ⇒ dPdz = −mgn(z).
Будем считать, что температура во всём цилиндре одинакова и равна Θ = kT.
Учитывая уравнение состояния P = nΘ, имеем:
dnn = −mgΘdz ⇒ n(z) = n(0)e−mgz/Θ = n(0)e−U(z)/Θ,
где U(z) - потенциальная энергия молекулы.
Эту барометрическую формулу в 1821 г. получил Пьер Лаплас. Умножим числитель и знаменатель под экспонентой
на число Авагадро NA, введя μ=mNA - молярную массу и газовую постоянную R=kNA.
Тогда для воздуха (азот μ=28г/моль) при T=273, имеем
n(z) = n(0)exp(−μgzRT) = n(0)exp(−2⋅14⋅10−3кг/моль⋅9.88.31⋅273z)=n(0)e−z/10км.
Заметим, что концентрация молекул падает тем быстрее, чем больше молярная масса.
Так как у кислорода 816O2 она несколько больше, чем у азота 714N2,
с высотой, в воздухе процентное содержание кислорода уменьшается.
Сделанное выше предположение о постоянстве температуры может показаться не очевидным (молекула, поднимаясь вверх и увеличивая свою потенциальную энергию, должна понижать кинетическую). Однако, численные моделирования показывают, что, действительно, температура молекул идеального газа в подобных условиях от z не зависит. Плотность вероятности нахождения на высоте z молекулы, имеющей с скорость v, разбивается на две независимые части: f(v,z) = f(v)mgΘe−mgz/Θ, где нормировочный множитель mg/Θ введен, чтобы интеграл по dz от 0, до ∞ (для сколь угодно высокого цилиндра). На самом деле, в реальной атмосфере температура воздуха зависит от множества факторов и с высотой уменьшается (в среднем на 6°C с каждым 1км).
Моделирование идеального газа
Поведение идеального газа несложно моделировать при помощи компьютера. Рассмотрим поведение шаров массами m1,m2 без учёта их вращения. При упругом столкновении сохраняется суммарный импульс и кинетическая энергия: m1v1+m2v2=m1v′1+m2v′2, m1v21+m2v22=m1v′21+m2v′22. Удобно перейти в систему отсчёта центра масс, в которой суммарный импульс шаров равен нулю. Пусть эта система движется со скоростью v и скорости шаров в ней равны ui. Тогда, требуя m1u1+m2u2=0, получаем: vi=ui+v, v=m1v1+m2v2m1+m2, u1=m2m1+m2(v1−v2). Так как u2=−m1u1/m2, кинетическая энергия в системе центра масс равна m1u21+m2u22 = m1(1+m1/m2)u21. Следовательно, после столкновения модули скоростей не изменяются: u2i=u′2i, а меняется лишь их направление.
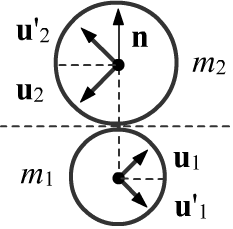
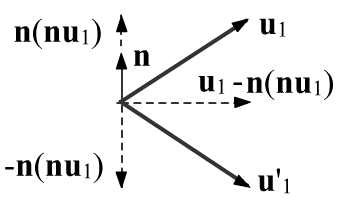 Пусть в момент касания шаров, единичный вектор между их центрами равен n=(r2−r1)/|r2−r1|.
В простейшем случае "гладких" шаров, при столкновении изменят направления компоненты
скоростей параллельных вектору n (рисунок справа):
u′1=u1−2n(nu1), u′2=u2+2n(nu2).
Несложно проверить, что длина векторов не изменилась: u2i=u′2i.
Пусть в момент касания шаров, единичный вектор между их центрами равен n=(r2−r1)/|r2−r1|.
В простейшем случае "гладких" шаров, при столкновении изменят направления компоненты
скоростей параллельных вектору n (рисунок справа):
u′1=u1−2n(nu1), u′2=u2+2n(nu2).
Несложно проверить, что длина векторов не изменилась: u2i=u′2i.
Таким образом, возвращаясь в лабораторную систему, имеем: v′1=v1−2m2nm1+m2n⋅(v1−v2), v′2=v2−2m1nm1+m2n⋅(v2−v1).