Теория вещества: 3. Статистический метод
Основные понятия
Микроскопическое состояние газа полностью определяется координатами и скоростями всех молекул в данный момент времени. В зависимости от задачи, можно рассматривать частичное микроскопическое описание состояние (например, только скорости).
Макроскопическое состояние газа в термодинамическом равновесии определяется переменными состояния: температурой T, давлением P и т.п. Одному и тому же макросостоянию может соответствовать множество микросостояний (обладающих одинаковой суммарной энергией).
Ансамбль систем - это совокупность систем, находящихся в одинаковых макроскопических состояниях и во всех возможных микроскопических состояниях. Различают:
- микроканонический ансамбль - совокупность "одинаковых", изолированных систем, имеющих равные энергии U, число частиц N и объёмы V;
- канонический ансамбль - совокупность систем, обменивающихся тепловой энергией Q с термостатом;
- большой канонический ансамбль - обмениваются с термостатом и тепловой энергией Q, и частицами N;
Постулат равновероятности микроскопических состояний (систем в ансамбле) лежит в основе статфизических рассуждений. Он эквивалентен эргодической гипотезе: вероятность нахождения молекулы в данном микросостоянии, вычисленная по ансамблю, совпадает с вероятностью, полученной при наблюдении за одной молекулой в одной системе в течении бесконечного времени.
Равновесному состоянию соответствует наибольшее число микросостояний. Например, пусть в сосуде есть N молекул и он мысленно разбит на две равные части с M молекулами в левой половине. Макросостояние с M=1 реализуется N микросостояниями (там находится любая из N молекул). Макросостоянию с M=N/2 соответствует максимальное число состояний CN/2N=N!/(N/2)!(N/2)! (см. ниже). Поэтому именно оно является равновесным, т.е. существенно чаще наблюдается в опыте.
Флуктуации концентрации
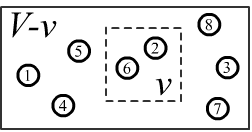 Пусть объёме газа V находится n молекул.
Выделим внутри небольшой объём v в котором находится m молекул.
Будем считать молекулы одинаковыми, но различимыми (их можно пронумеровать).
Справа на рисунке приведено одно возможное микросостояние системы с макропараметрами m=2, n=8.
При этом мы интересуемся лишь номерами частиц, попавших в выделенный объём,
а не их точным положением и скоростью.
Пусть объёме газа V находится n молекул.
Выделим внутри небольшой объём v в котором находится m молекул.
Будем считать молекулы одинаковыми, но различимыми (их можно пронумеровать).
Справа на рисунке приведено одно возможное микросостояние системы с макропараметрами m=2, n=8.
При этом мы интересуемся лишь номерами частиц, попавших в выделенный объём,
а не их точным положением и скоростью.
Вероятность того, что данная молекула окажется в объёме v равна p=v/V. Вероятность того, что она там не окажется обозначим через q=1−p. Вероятность попасть в объём v в точности m молекулам, а остальным n−m туда не попасть равна pmqn−m. Это возможно сделать Cmn способами (см. сноску ниже). Другими словами существует Cmn равновероятных микросостояний, соответствующих макросостоянию (m,n).
Таким образом, вероятность нахождения m частиц в объёме v имеет биномиальное распределение: Pn(m)=Cmnpmqn−m, q=1−p, n∑m=0Pn(m)=(p+q)n=1.
При помощи бинома Ньютона, несложно получить производящую функцию для средних:
⟨mk⟩ = n∑m=0mkPn(m), (pet+q)n = n∑m=0Cmnetmpmqn−m = ⟨etm⟩ = ∞∑k=0⟨mk⟩tkk!,
где последнее равенство получено разложением экспоненты в ряд Тейлора. Беря производные по t
от (pet+q)n в точке t=0, получаем следующие выражения для среднего,
дисперсии,
и скоса (асимметрии):
ˉm=⟨m⟩=np, D=⟨(m−ˉm)2⟩=npq, ⟨(m−ˉm)3⟩D3/2=1−2p√npq.
Корень из дисперсии D характеризует типичные
отклонения числа частиц от их среднего значения ˉm.
Чем ближе скос к нулю, тем симметричнее распределение относительно среднего значения.
Запишем относительное отклонение от среднего числа частиц, которое характеризует флуктуацию концентрации (отношение корня из дисперсии к среднему): δmˉm = D1/2ˉm = √npqnp = √q/pn = √Vv−1⋅1√n → 1√ˉm, где предел записан для v≪V. В кубическом метре газа при стандартных условиях содержится 44 моля или порядка 1025 молекул. Поэтому даже в одном кубическом миллиметре будет ˉm=1016 молекул. Таким образом постоянство концентрации газа в равновесном состоянии соблюдается с колоссальной точностью.
✒ Биномиальные коэффициенты Cmn равны числу способов выбрать m различимых ("нумерованных") объектов из совокупности, состоящей из n объектов. Первый из m можно выбрать n способами, затем второй n−1 способами и т.д. Поэтому получаем n(n−1)...(n−m+1) способов. Так как порядок в котором отобраны объекты не важен, это число делим на m! (число перестановок m объектов). В результате: Cmn=n!m!(n−m)!, Cmn=Cn−mn, Cm+1n+1−Cm+1n=Cmn. Бином Ньютона является производящей функцией для Cmn (ряд Тейлора для (1+x)n по x даёт Cmn): (1+x)n = 1+n1!x+n(n−1)2!x2+...+xn = n∑m=0Cmnxm.
Распределение Пуассона
Пусть n→∞ и p→0 так, что np=nv/V=λ=const.
Так как n/V - это концентрация молекул во всём объёме, параметр λ равна среднему числу молекул в объёме v.
Запишем биномиальное распределение:
Pn(m)=n(n−1)...(n−m+1)m!pmqn−m=(np)mqn−mm!(1−1n)...(1−m−1n)
 и устремим n→∞ и p→0. Тогда qn−m→qn=(1−λ/n)n→e−λ (замечательный предел) и
мы приходим к распределению Пуассона:
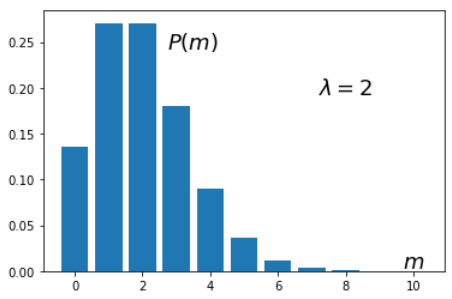
P(m)=λmm!e−λ, ∞∑m=0P(m)=eλe−λ=1.
Параметр распределения λ, обычно, находится из опыта.
Он равен среднему значению ˉm=λ и дисперсии D=⟨(m−ˉm)2⟩=λ,
что следует при n→∞, p→0 из статистик для биномиального распределения. Скос равен λ−1/2.
и устремим n→∞ и p→0. Тогда qn−m→qn=(1−λ/n)n→e−λ (замечательный предел) и
мы приходим к распределению Пуассона:
P(m)=λmm!e−λ, ∞∑m=0P(m)=eλe−λ=1.
Параметр распределения λ, обычно, находится из опыта.
Он равен среднему значению ˉm=λ и дисперсии D=⟨(m−ˉm)2⟩=λ,
что следует при n→∞, p→0 из статистик для биномиального распределения. Скос равен λ−1/2.
Нормальное распределение
✒ Рассмотрим теперь предел больших n и конечных p (v≈V/2) при m∼np=⟨m⟩ (m находится около своего среднего значения). Найдём сначала разложение в ряд по x факториала (N+x)! при N≫x. По определению: ln(N+x)!=ln[N!(N+1)...(N+x)]=lnN!+x∑k=1ln(N+k)=lnN!+xlnN+x∑k=1ln(1+kN). Учитывая разложение ln(1+x)=x+... при малых x и сумму 1+2+...+x=x(x+1)/2 (арифметическая прогрессия), окончательно получаем: ln(N+x)!=lnN!+xlnN+x(x+1)2N+O(1N2).
Пусть x, равен отклонению m от среднего значения np. При этом m=pn+x и n−m=qn−x: lnPn(m)=lnn!−ln(pn+x)!−ln(qn−x)!+(pn+x)lnp+(qn−x)lnq. Используя формулу для ln(N+x)!, получаем: lnPn(m) ≈ lnPn(np)−x2+(1−2p)x2D, где первое слагаемое соответствует постоянным членам разложения при x=0 и D=npq - дисперсия биномиального распределения. Множитель 1−2p при линейном по x члене меняется в интервале (−1,...,1) и характеризует асимметрию биномиального распределения. Это слагаемое даёт небольшой вклад (и при p=1/2 пропадает). Действительно, так как x=1,2,3,..., имеем x2≫(1−2p)x уже для x=2 (например, для p=1/4 будет 4≫1). Чем больше x, тем меньше вклад этого слагаемого.
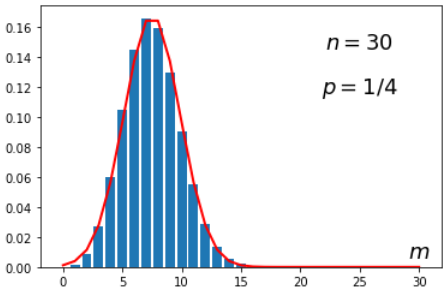 Таким образом, хорошим приближением к биномиальному распределению при больших n и p∼1/2
является нормальное или гауссово распределение:
Pn(m)≈1√2πDe−(m−np)2/2D,
где нормировочный множитель 1/√2πD получен
интегрированием по x от −∞, до ∞
(экспонента быстро убывает). Такое распределение названо "нормальным",
потому, что оно часто возникает в различных практических задачах. Например,
если измеряются значения некоторой величины X, которая подвержена большому числу
случайных и независимых внешних воздействий, она становится случайной с нормальным распределением.
Таким образом, хорошим приближением к биномиальному распределению при больших n и p∼1/2
является нормальное или гауссово распределение:
Pn(m)≈1√2πDe−(m−np)2/2D,
где нормировочный множитель 1/√2πD получен
интегрированием по x от −∞, до ∞
(экспонента быстро убывает). Такое распределение названо "нормальным",
потому, что оно часто возникает в различных практических задачах. Например,
если измеряются значения некоторой величины X, которая подвержена большому числу
случайных и независимых внешних воздействий, она становится случайной с нормальным распределением.
Нормальное распределение для скоростей
Компоненты скорости молекул v={vx,vy,vz} являются независимыми случайными величинами с нормальным распределением. Продемонстрируем это следующим образом. Пусть в начальный момент времени молекула имеет нулевую скорость. Так как она постоянно испытывает толчки со стороны других молекул, через некоторое время её скорость может принять произвольное значение. Рассмотрим для краткости 2-мерный случай и введём функцию плотности распределения вероятностей w(vx,vy). Изменение скорости вдоль каждой оси происходят независимым и схожим образом. Кроме этого, толчки в среднем передают нулевую скорость, поэтому плотность вероятности должна быть чётной функцией скоростей. Таким образом, будем считать, что w(vx,vy)=w(v2x)w(v2y).
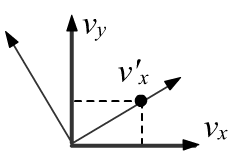 Повернём систему координат так, чтобы ось v′x проходила через текущее положение частицы.
В новых координатах плотность вероятностей равна w(v′2x)w(0), где v′2x=v2x+v2y.
Вероятность (получаемая умножением плотности на элементарный объём dvxdvy)
не должна зависеть от подобных поворотов, что приводит к следующему функциональному уравнению:
w(v2x+v2y)w(0) = w(v2x)w(v2y).
Повернём систему координат так, чтобы ось v′x проходила через текущее положение частицы.
В новых координатах плотность вероятностей равна w(v′2x)w(0), где v′2x=v2x+v2y.
Вероятность (получаемая умножением плотности на элементарный объём dvxdvy)
не должна зависеть от подобных поворотов, что приводит к следующему функциональному уравнению:
w(v2x+v2y)w(0) = w(v2x)w(v2y).
Оно легко решается, если обозначить x=v2x и f(x)=lnw(v2x) и аналогично для y. В этих обозначениях уравнение имеет вид f(x+y)+f(0) = f(x)+f(y). Вычислим его частную производную по y при y=0: f′(x)=f′(0). Отсюда следует, что f(x) - линейная функция аргумента и поэтому w(v2x)=w(0)exp(±αv2x), где α - некоторая положительная констната. Физический смысл имеет знак минус (очень большие скорости маловероятны). Поэтому окончательно: w(v2x)=√απe−αv2x, ∞∫−∞w(v2x)dvx = 1, где множитель w(0) вычислен из условия нормировки (интеграл по всем скоростям равен 1).
Распределение Максвелла
Для дальнейшего удобно переопределить константу α следующим образом: α=βm/2. Плотность распределения вероятностей скоростей в трёхмерном случае w(v)=w(v2x)w(v2y)w(v2z) имеет вид: w(v)=(mβ2π)3/2e−βε(v2), ε(v2)=mv22.
Вычислим среднюю энергию молекулы: ⟨ε(v2)⟩ = ∫mv22w(v)d3v = m2(mβ2π)1/23∞∫−∞v2xe−βmv2x/2dvx=3/2β. Так как для идеального газа, по определению, ⟨ε⟩=(3/2)kT, получаем, что, β=1/kT - обратная температура. В сферических координатах элемент объёма равен d3v=dΩ,v2dv, где v=|v|. При интегрировании по телесному углу Ω имеем d3v↦4πv2dv. Поэтому плотность распределения модуля скорости имеет вид: w(v)=4π(mβ2π)3/2v2e−βmv2/2, ∞∫0w(v)dv = 1. При помощи этой плотности несложно найти характерные значения скоростей молекул газа: ˉv=⟨v⟩ = √8kTπm, √⟨v2⟩ = √3kTm, vmax = √2kTm, где последняя - это скорость максимума плотности w(v). Относительная флуктуация скорости вокруг среднего: δvˉv = √⟨(v−ˉv)2⟩ˉv = √⟨v2⟩−ˉv2ˉv = √3π8−1 ≈ 0.42.
Аналогично несложно несложно получить распределение для энергии: w(v)dv=(w(v)/mv)dε, с v=√2ε/m: w(ε)=β3/2√π/2 √ε e−βε, ⟨ε⟩ = 3/2β = 32kT, εmax = 1/2β. То, что среднее ⟨ε⟩ в три раза больше скорости максимума распределения εmax говорит о наличии справа длинного хвоста у распределения w(v).
Распределение Гиббса
Полезные интегралы
✒ При работе с нормальным распределением часто возникает интеграл следующего вида:
I=∞∫−∞e−x2dx.
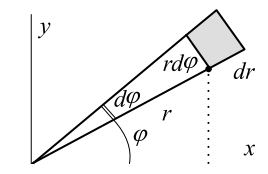 Он вычисляется в полярных координатах (r, ϕ): x=rcosϕ, y=rsinϕ, как двойной:
I2=∞∫−∞∞∫−∞e−x2−y2dxdy=2π∫0∞∫0e−r2rdrdϕ=2π∞∫0e−r2dr22=π,
где мы воспользовались тем, что в координатах (r, ϕ) элемент площади равен произведению дуги rdϕ
на изменение радиуса dr: dxdy=rdϕdr.
Извлекая квадратный корень и делая замену x→x√α, получаем:
I(α)=∞∫−∞e−αx2dx=√πα.
Полезный приём - взятие производных правой и левой частей по параметру α для получения интегралов от чётных степеней x2n.
Интеграл от нечетных степеней x равен нулю (асимметричность).
Он вычисляется в полярных координатах (r, ϕ): x=rcosϕ, y=rsinϕ, как двойной:
I2=∞∫−∞∞∫−∞e−x2−y2dxdy=2π∫0∞∫0e−r2rdrdϕ=2π∞∫0e−r2dr22=π,
где мы воспользовались тем, что в координатах (r, ϕ) элемент площади равен произведению дуги rdϕ
на изменение радиуса dr: dxdy=rdϕdr.
Извлекая квадратный корень и делая замену x→x√α, получаем:
I(α)=∞∫−∞e−αx2dx=√πα.
Полезный приём - взятие производных правой и левой частей по параметру α для получения интегралов от чётных степеней x2n.
Интеграл от нечетных степеней x равен нулю (асимметричность).
✒ Вычислим ещё один интеграл, взяв от него n раз производную по α:
I(α)=∞∫0e−αxdx=−1α e−αx|∞0=1α ⇒ ∞∫0xne−αxdx=n!αn+1.
Интегралы такого типа встречаются часто и для них введено специальное
обозначение в виде гамма-функции:
Γ(z)=∞∫0xz−1e−xdx.
Интегрируя по частям, убеждаемся, что Γ(z+1)=zΓ(z).
В частности, для целых аргументов: Γ(n+1)=n!.
Для полуцелых аргументов гамма-функция сводится к гауссовому интегралу. Так, Γ(1/2)=√π.
✒ Из интегрального определения гамма-функции следует формула Стирлинга. Представим xne−x как ef(x). Функция f(x)=−x+nlnx имеет максимум в точке x0=n, так как f′(x0)=−1+n/x0=0. Разложим её в ряд по x−x0: f(x)=f(n)+12f″(n)(x−n)2+... = −n+nlnn−(x−n)22n+... Поэтому n!≈e−n+nlnn∞∫0e−(x−n)22ndx≈e−n+nlnn∞∫−∞e−(x−n)22ndx=e−n+nlnn√2πn. Во втором интеграле нижний предел заменён на −∞, так как при большом n максимум экспоненты уходит далеко вправо и становится всё более узким, поэтому интеграл от −∞ до 0 практически равен нулю.