Четырёхмерное пространство-время
| Прецессия ускоренного стрежня << | Оглавление (Глава 2) | >> Ковариантная формулировка |
|---|
Перейдём теперь к геометрическим аспектам теории относительности. Рассмотрим поворот координатных осей на угол . Координаты одной и той же точки в исходной и повёрнутой декартовых системах связаны следующим образом:

Эти преобразования получаются из элементарных геометрических соображений. Заштрихованные на рисунке углы двух подобных прямоугольных треугольников равны . Поэтому вертикальная линия, опущенная из точки и имеющая длину , состоит из двух отрезков: гипотенузы верхнего треугольника и катета нижнего. Их сумма даёт второе уравнение преобразования. Аналогично (проекция точки на ось ) состоит из катета и гипотенузы , откуда получается первое уравнение. Поворот осей оставляет неизменным расстояние, например от начала координат .
Преобразования Лоренца имеют похожий линейный вид:
где введены гиперболические косинус и синус , так, что . В силу их свойств (стр. \pageref{m_hyperbol}):
Учитывая, что , , при помощи мнимой единицы , преобразованиям Лоренца можно придать вид, формально совпадающий с поворотом в обычном пространстве:
Если считать декартовыми координатами , то эти преобразования являются поворотами координатных осей на мнимый угол . При этом неизменным остаётся квадрат расстояния от начала координат:
который с точностью до знака совпадает с интервалом между двумя событиями в точке и (стр. \pageref{bk_h_ds_inv}). Пространство с подобными необычными свойствами называют псевдоевклидовым пространством.
Общий подход к понятию "пространство" состоит в рассмотрении абстрактного множества точек. Для их "нумерации" можно использовать наборы чисел , называемых координатами. Число называется размерностью пространства. Пока рассматривается абстрактная совокупность точек, не существует понятия близости двух точек. Наличие координат само по себе такой меры близости не даёт, так как нумерация точек может быть достаточно произвольной. Поэтому первый шаг по превращению множества точек в пространство совершается, когда задают расстояние между двумя бесконечно близкими точками. В 3-мерном евклидовом пространстве такое расстояние имеет вид:
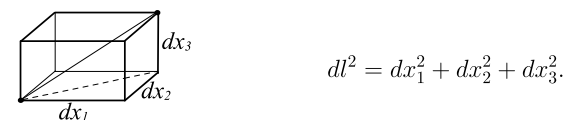
Оно имеет привычную геометрическую интерпретацию в виде теоремы Пифагора, связывающей диагональ параллелепипеда, построенного на смещениях по каждой координате , , . Если расстояние равно нулю , то это означает, что точки совпадают. Использование бесконечно близких точек для определения расстояния удобно при переходе к пространствам, обладающим кривизной. Перед квадратами дифференциалов координат в евклидовом расстоянии стоят знаки плюс. Говорят, что оно имеет сигнатуру .
Если расстояние задано другим способом, то может получится иное пространство, со свойствами отличающимися от евклидового. Рассмотрим 4-мерное пространство, точки которого будем называть событиями и нумеровать координатами . Обозначим бесконечно малое расстояние в этом пространстве как и определим его следующим образом:
Оно имеет сигнатуру . За исключением этого оно похоже на евклидово расстояние в декартовых координатах, поэтому его называют псевдоевклидовым. Близость двух точек в таком пространстве оказывается достаточно своеобразной. Например, нулевое расстояние не означает, что точки совпадают (см. стр. \pageref{bk_h_ds_inv}). Кроме этого, не смотря на формальное наличие квадрата, может быть и отрицательным.
В старых книгах по теории относительности активно использовалась мнимая единица для придания псевдоевклидовому расстоянию вид евклидового: . Такое "заметание под ковёр" псевдоевклидовости не является разумным и сейчас редко используется.
Координатные оси и другие геометрические объекты 2-мерного евклидового пространства легко изображать на плоскости так как она является физическим воплощением такого пространства. С псевдоевклидовым пространством даже в двух измерениях не всё так просто. Тем не менее нарисуем две перпендикулярные оси. По вертикальной будем откладывать время события , а по горизонтальной его координату . Равномерное и прямолинейное движение со скоростью будем изображать в виде прямой (первый рисунок):

Медиана (средняя линия) между координатными осями соответствует распространению светового сигнала. Все остальные траектории, выходящие из , оказываются сильнее прижатыми к координатной оси по сравнению с медианой, так как физические скорости .
Координата и время некоторого события (точка на втором рисунке) определяются аналогично евклидовым декартовым координатам, при помощи координатной сетки. Она проводится в виде линий (пунктиры), параллельных каждой координатной оси. Это означает что ось имеет уравнение , а ось , соответственно, . Сетка формируется при помощи горизонтальных и вертикальных прямых.
Изобразим на этой же плоскости оси () системы отсчёта , движущейся относительно со скоростью . Если в момент начала систем отсчёта совпадали , то траектория часов, расположенных в начале координат системы , имеет вид прямой . Она является координатной осью . Аналогично, линия соответствует координатной оси и имеет уравнение . Она наклонена к оси на такой же угол, как ось к (третий рисунок).
Таким образом, пространственная и временная оси системы , изображённые на плоскости системы будут выглядеть сплюснутыми вокруг медианы (траектория светового сигнала). Эта же траектория будет медианой и в системе . Координатная сетка системы также сплюснута. Временные линии координатной сетки, параллельные оси имеют уравнения или . Аналогично для пространственных линий сетки .
Важно помнить, что событие (точка в пространстве-времени) существует само по себе и не зависит от выбора системы координат (точнее системы отсчёта). Его же описание (координаты) будут разными в разных системах. Точно также при повороте евклидовой плоскости координаты меняются, но точка пространства остаётся неизменной.
Наличие координатной сетки различных систем отсчёта позволяет легко получать координаты события. Например, два события одновременные в системе должны находится на горизонтальной прямой . События одновременные в находятся на прямых которые наклонены к прямым . Это является геометрической иллюстрацией относительности одновременности.
Чтобы ввести на плоскости геометрию, зададим расстояние между двумя точками , равное интервалу между событиями. Для "евклидовой интуиции" это очень необычное расстояние. Нарисуем, например, евклидову и псевдоевклидову единичные окружности, как множество точек равноудалённых от центра (ниже начало координат):

В псевдоевклидовом пространстве единичная окружность — это гипербола . На большом расстоянии от начала координат гипербола стремится к траекториям светового сигнала , испущенного из точки .
Также как обычная окружность на евклидовой плоскости определяет тригонометрические функции синуса и косинуса, так и окружность в псевдоевклидовом пространстве ("псевдоокружность") определяет гиперболические синус и косинус , как проекции точки псевдоокружности на ось и . При этом проектируемая на оси гипотенуза прямоугольного треугольника имеет меньшую длину , чем катет ! Вместо евклидовой теоремы Пифагора мы имеем псевдоевклидову теорему .
Вообще, изображение на евклидовой плоскости псевдоевклидового пространства выглядит несколько неуклюже, и наилучшей физической моделью псевдоевклидового пространства является не лист бумаги, а само пространство-время.
До сих пор мы рассматривали 2-мерное псевдоевклидово пространство. В реальности оно 4-мерно, однако на листе бумаги можно изобразить не более трёх измерений . В этом случае световые сигналы являются световым конусом, а псевдоокружность становится псевдосферой или в терминах евклидового пространства — гиперболоидом (первый рисунок):

Если в евклидовом пространстве квадрат расстояния всегда положителен, то в псевдоевклидовом он может быть и отрицательным. Поэтому существует две единичные сферы и . Псевдосфера мнимого радиуса является односвязной и также асимптотически стремится к световому конусу (второй рисунок).
Так как любая частица имеет скорость меньше скорости света, события, причинно связанные с событием в точке находятся внутри светового конуса. Причинность означает, что существует возможное влияние одного события на второе при помощи движения между ними некоторого агента со скоростью, меньшей, чем фундаментальная.
Траектория частицы, пролетевшей в момент времени точку всё время находится внутри светового конуса. При этом касательная к этой траектории всегда находится внутри локальных конусов, построенных к произвольной точке траектории (третий рисунок).
В силу свойств псевдоевклидового расстояния, длина элемента траектории будет меньше, чем длина траектории частицы, остававшейся неподвижной в точке (ось ). Хотя на евклидовой плоскости это расстояние и выглядит длиннее. Поэтому переносить привычную евклидову интуицию на псевдоевклидовые пространственно-временные диаграммы необходимо очень осторожно.
Верхнюю внутреннюю часть конуса называют множеством абсолютно будущих событий относительно , а нижнюю — множеством абсолютно прошлых событий. Пространство вне конуса называется множеством абсолютно удалённых событий.
Рассмотрим геометрические интерпретации некоторых кинематических эффектов. Несмотря на некоторые сложности в восприятии псевдоевклидовой плоскости подобный геометрический анализ теории относительности обладает определённой наглядностью.

Пусть наблюдается два "тика" часов, неподвижных в системе в точке . Первое событие происходит в начале координат , а второе расположено на оси (выше первый рисунок). Если второй "тик" происходит в момент времени , то это же событие имеет координату (гиперболическая проекция) Так как мы приходим к релятивистскому замедлению времени. То, что можно увидеть, проведя псевдосферу, отсекающую на осях и одинаковые единицы времени (отрезки единичной длины). На рисунке видно, что 1 на оси лежит на рисунке ниже, чем проекция события (точка на рисунке).
Аналогично анализируется сокращение длины (выше второй рисунок). Предположим, что стержень единичной длины неподвижен в системе (отрезок ). Его левый конец находится в начале координат и имеет траекторию, совпадающую с осью . Траектория правого конца стержня ей параллельна. Измерение длины стрежня производится в системе путём одновременной фиксации его начала и конца. Одновременные события и имеют одинаковое время в системе , но различное в . Проекция точек и на ось будет равна длине стержня в системе . Видно, что эта проекция короче, чем единица длины, отсекаемая псевдокружностью (в данном случае, имеющей длину -1).
На третьем рисунке иллюстрируется эффект Доплера. Источник света, находящийся в начале координат испускает световые сигналы. Первый в момент времени , а второй, спустя время . В начало отсчёта системы он попадёт, когда траектория света (тонкая линия ) пересечёт ось . Это время оказывается больше как единицы длины на оси , отсекаемой единичной псевдосферой, так и проекции события испускания сигнала (пунктир).
| Прецессия ускоренного стрежня << | Оглавление (Глава 2) | >> Ковариантная формулировка |
|---|
Релятивистский мир - лекции по теории относительности, гравитации и космологии




























































































