Рассматривая электродинамику, мы различали поля и частицы. Частицы мыслились как некоторые компактные (возможно точечные) образования, которые взаимодействовали при помощи электромагнитного поля. Таким образом, основное различие между полем и частицами состоит в том, что энергия последних локализована в малой области пространства, тогда как энергия поля существенно более нелокальная.
Оказывается, что в рамках нелинейных полевых теорий можно получать решения, которые обладают локализованной энергией, движущейся в пространстве. Такие сгустки энергии могут взаимодействовать друг с другом, сохраняя после взаимодействия свою форму, образовывать связанные состояния и т.д. Подобные решения, называемые солитонами, могут служить полевой моделью частиц.
Рассмотрим простейший пример теории действительного скалярного поля с лагранжианом:

Уравнения Лагранжа

приводят к следующим уравнениям движения:

|
(EQN)
|
Тензор энергии-импульса находится по общей формуле (), стр.\,\pageref{neter_energey_momentum}, которая в случае скалярного поля имеет вид:

Подставляя лагранжиан, получаем симметричный тензор:

Плотность энергии поля  имеет вид:
имеет вид:

|
(EQN)
|
а плотность импульса  :
:

|
(EQN)
|
где точка над функцией поля — это производная по времени.
Солитонное решение для скалярного поля существует, например, в одномерном случае  для:
для:

где  и
и  — некоторые константы. Такой лагранжиан называют моделью Хиггса. Для него уравнения движения () имеют вид:
— некоторые константы. Такой лагранжиан называют моделью Хиггса. Для него уравнения движения () имеют вид:

|
(EQN)
|
Обратим внимание, что знак перед квадратичным членом отличается от массивного линейного поля, которе рассматривалось на стр.\,\pageref{field_scalar2_lag}. Без потери общности можно положить  . Действительно, заменами
. Действительно, заменами  и
и  уравнение () можно привести к форме с
уравнение () можно привести к форме с  . Обратные замены — восстанавливают эти константы.
. Обратные замены — восстанавливают эти константы.
Мы планируем получить сгусток энергии скалярного поля, который движется с постоянной скоростью  по траектории
по траектории  . Если вместе с ним с той же скорость будет двигаться наблюдатель, он увидит статическую конфигурацию поля, не зависящую от времени. Подставляя
. Если вместе с ним с той же скорость будет двигаться наблюдатель, он увидит статическую конфигурацию поля, не зависящую от времени. Подставляя  в уравнения движения (), получаем:
в уравнения движения (), получаем:

где  . Это обыкновенное дифференциальное уравнение второго порядка. Умножая обе части на
. Это обыкновенное дифференциальное уравнение второго порядка. Умножая обе части на  и интегрируя, имеем:
и интегрируя, имеем:

где константа интегрирования выбрана равной  . Извлекая корень, разделяя переменные и интегрируя это уравнение еще раз
. Извлекая корень, разделяя переменные и интегрируя это уравнение еще раз

получаем решение:

|
(EQN)
|
где  — еще одна константа интегрирования (начальное положение фазы солитона при
— еще одна константа интегрирования (начальное положение фазы солитона при  ). Для восстановления размерных констант аргумент гиперболического тангенса нужно умножить на
). Для восстановления размерных констант аргумент гиперболического тангенса нужно умножить на  , а сам тангенс на
, а сам тангенс на  .
.
Плотность энергии поля () для решения () равна:

Плотность импульса связана с плотностью энергии обычным образом:  . Интегрирование по всему пространству дает полную энергию:
. Интегрирование по всему пространству дает полную энергию:

где константу (в которой восстановлены параметры  и
и  )
)

можно интерпретировать как массу солитона.
Типичный размер области с отличной от нуля энергией поля пропорционален  . Чем больше параметр
. Чем больше параметр  тем компактнее получается солитон и тем больше будет его масса. Параметр
тем компактнее получается солитон и тем больше будет его масса. Параметр  влияет на высоту солитона и чем он меньше, тем выше будет плотность энергии.
влияет на высоту солитона и чем он меньше, тем выше будет плотность энергии.
В 3-мерном пространстве получается аналогичное решение, но его энергия локализована только в направлении движения. В перпендикулярных направлениях убывания плотности энергии нет. Существенным в этой модели является также наличие нелинейности. Линейное уравнение Клейна-Гордона с  решений вида
решений вида  c локализованной в пространстве плотностью энергии не имеет.
c локализованной в пространстве плотностью энергии не имеет.
В общем случае, энергия солитона (интеграл от ()) будет конечной, если на бесконечности поле стремится к значению  для которого
для которого  . Такое значение поля называют классическим вакуумом. Лагранжиан, рассмотренный выше, имеет два таких вакуума:
. Такое значение поля называют классическим вакуумом. Лагранжиан, рассмотренный выше, имеет два таких вакуума:  . Они соответствуют двум минимумам
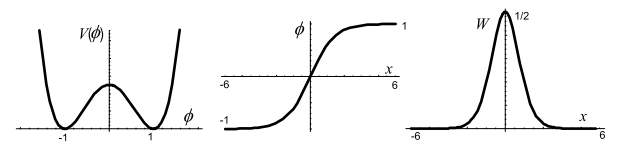
. Они соответствуют двум минимумам  (см. выше первый рисунок). Справа от солитона поле стремиться к одному из этих вакуумов, а слева — ко второму. В результате, хотя само поле не убывает на бесконечности, плотность энергии оказывается локализованной в пространстве, а суммарная энергия — конечной.
(см. выше первый рисунок). Справа от солитона поле стремиться к одному из этих вакуумов, а слева — ко второму. В результате, хотя само поле не убывает на бесконечности, плотность энергии оказывается локализованной в пространстве, а суммарная энергия — конечной.
 Еще одна модель, допускающее солитонное решение с нелинейностью
Еще одна модель, допускающее солитонное решение с нелинейностью

приводит к уравнению синус-Гордона:

|
(EQN)
|
Повторяя вычисления ( \,H), аналогичные предыдущей модели, получаем решение в виде движущегося солитона:
\,H), аналогичные предыдущей модели, получаем решение в виде движущегося солитона:

|
(EQN)
|
с локализованной плотностью энергии:

и импульсом  . Масса такого солитона равна
. Масса такого солитона равна  . Форма нелинейной функции
. Форма нелинейной функции  , решение и плотность энергии в системе покоя солитона (
, решение и плотность энергии в системе покоя солитона ( ) приведены на рисунках ниже:
) приведены на рисунках ниже:

В обоих моделях локализованной оказалась плотность энергии, но не поле. В модели Хиггса поле изменяется от  до
до  . В синус-Гордоне от 0 до
. В синус-Гордоне от 0 до  . Оба значения являются классическими вакуумами модели. Такие солитоны называются кинками (kink — изгиб). В модели Хиггса классических вакуумов только 2 в модели синус-Гордона их бесконечно много, причем существует обычный вакуум нулевого поля
. Оба значения являются классическими вакуумами модели. Такие солитоны называются кинками (kink — изгиб). В модели Хиггса классических вакуумов только 2 в модели синус-Гордона их бесконечно много, причем существует обычный вакуум нулевого поля  .
.
Решения подобные кинкам часто называют топологическими. Это название связано с перечислением способов отождествления двух предельных точек  и классических вакуумов системы. Такие отожествления можно представить в виде линий, соединяющих предельные точки и вакуумы. Переплетение таких линий обладает определенной топологией (имеет ряд свойств, не зависящих от расстояний и других геометрических свойств). Для одномерного скалярного поля топология достаточно тривиальна, однако в более сложных моделях она может оказаться уже не такой простой.
и классических вакуумов системы. Такие отожествления можно представить в виде линий, соединяющих предельные точки и вакуумы. Переплетение таких линий обладает определенной топологией (имеет ряд свойств, не зависящих от расстояний и других геометрических свойств). Для одномерного скалярного поля топология достаточно тривиальна, однако в более сложных моделях она может оказаться уже не такой простой.
 Солитоны достаточно устойчивые образования и небольшие внешние возмущения их не разрушают. Рассмотрим соответствующее условие устойчивости \cite{Rubakov2010}. Пусть поле равно
Солитоны достаточно устойчивые образования и небольшие внешние возмущения их не разрушают. Рассмотрим соответствующее условие устойчивости \cite{Rubakov2010}. Пусть поле равно  , где
, где  — солитонное решение, а
— солитонное решение, а  — небольшое возмущение. Подставим эту сумму в уравнение движения и разложим в ряд по
— небольшое возмущение. Подставим эту сумму в уравнение движения и разложим в ряд по  :
:

Так как солитон  удовлетворяет уравнению
удовлетворяет уравнению  , возмущение в системе отсчета, где солитон неподвижен (
, возмущение в системе отсчета, где солитон неподвижен ( ) должно удовлетворять линейному уравнению:
) должно удовлетворять линейному уравнению:

Будем искать его решение в виде  . Тогда
. Тогда  удовлетворяет дифференциальному уравнению второго порядка:
удовлетворяет дифференциальному уравнению второго порядка:

|
(EQN)
|
где  . Потребуем, чтобы функция
. Потребуем, чтобы функция  на бесконечности убывала (возмущение только в окрестности максимума плотности энергии солитона). Подобная задача с граничными условиями
на бесконечности убывала (возмущение только в окрестности максимума плотности энергии солитона). Подобная задача с граничными условиями  называется задачей Штурма — Лиувилля. В квантовой механике ей соответствует стационарное уравнение Шредингера с потенциалом
называется задачей Штурма — Лиувилля. В квантовой механике ей соответствует стационарное уравнение Шредингера с потенциалом  и энергией
и энергией  . Граничные условия приводят к тому, что значения частот
. Граничные условия приводят к тому, что значения частот  ограничены снизу и могут принимать дискретные значения. Если
ограничены снизу и могут принимать дискретные значения. Если  (
( — действительно), то возмущения не растут со временем. Если же существует хотя бы одно отрицательное
— действительно), то возмущения не растут со временем. Если же существует хотя бы одно отрицательное  , то
, то  и с течением времени солитонное решение
и с течением времени солитонное решение  будет разрушаться экспоненциально растущим во времени возмущением.
будет разрушаться экспоненциально растущим во времени возмущением.
Для модели Хиггса (H) и синус-Гордона (SG), получаются следующие "потенциалы":

Их собственные значения неотрицательны, поэтому соответствующие солитоны устойчивы. Заметим, что минимальная частота в обоих случаях равна нулю. Действительно, в системе покоя  удовлетворяет уравнению
удовлетворяет уравнению  . Дифференцируя его по
. Дифференцируя его по  , получаем () с
, получаем () с  и
и  .
.
Аналогичным образом анализируется устойчивость в более сложных моделях. Подобная устойчивость решения в математике называется устойчивостью по Ляпунову.
 Полученный критерий устойчивости (
Полученный критерий устойчивости ( ) работает только при малых возмущениях. Однако оказывается, что в ряде случаев солитоны сохраняют свою форму и после достаточно сильных потрясений. Эволюцию произвольного решения нелинейного уравнения удобно анализировать численно при помощи компьютера. Для этого необходимо задать начальные условия
) работает только при малых возмущениях. Однако оказывается, что в ряде случаев солитоны сохраняют свою форму и после достаточно сильных потрясений. Эволюцию произвольного решения нелинейного уравнения удобно анализировать численно при помощи компьютера. Для этого необходимо задать начальные условия  и
и  и затем, аппроксимируя производные при помощи конечных разностей, находить решение в произвольный момент времени. Для этого непрерывное 2-мерное пространство
и затем, аппроксимируя производные при помощи конечных разностей, находить решение в произвольный момент времени. Для этого непрерывное 2-мерное пространство  заменяют дискретной сеткой с малым шагом
заменяют дискретной сеткой с малым шагом  по оси времени и
по оси времени и  — по оси координат. Соответственно поле
— по оси координат. Соответственно поле  является массивом
является массивом  . Частные производные заменяются разностями:
. Частные производные заменяются разностями:

Подставляя их в уравнение движения (), получаем:

Задав начальные условия  и
и  при помощи этого соотношения для каждой координаты
при помощи этого соотношения для каждой координаты  получаются
получаются  . Аналогично, двигаясь по оси
. Аналогично, двигаясь по оси  находим поле в произвольный момент времени. Естественно, это простейший метод и он может быть улучшен при помощи самых различных приемов \cite{Mahankov1983}.
находим поле в произвольный момент времени. Естественно, это простейший метод и он может быть улучшен при помощи самых различных приемов \cite{Mahankov1983}.
Рассмотрим в качестве примера столкновение кинка и антикинка в модели синус-Гордона. Кинк соответствует знаку плюс в решении (), а антикинк — минусу. Несмотря на нелинейность уравнения сложим эти два решения и воспользуемся полученной функцией в качестве начальных условий  и
и  . Численное моделирование приводит к следующим четырем кадрам столкновения двух солитонов, движущихся навстречу со скоростями
. Численное моделирование приводит к следующим четырем кадрам столкновения двух солитонов, движущихся навстречу со скоростями  и
и  (изображена плотность энергии системы
(изображена плотность энергии системы  ):
):

Видно, что после столкновения солитоны восстанавливают свою форму и продолжают двигаться с теми же скоростями, что и до столкновения.
 Выше мы искали решения нелинейных полевых уравнений в виде
Выше мы искали решения нелинейных полевых уравнений в виде  . В системе покоя (
. В системе покоя ( ) это решение является статическим (не зависит от
) это решение является статическим (не зависит от  ). Оказывается, что существую динамические солитонные решения, которые в системе покоя испытывают периодические колебания. Такие решения называют бризерами (от английского breathe - дышать). Будем искать решение уравнения синус-Гордона () в виде
). Оказывается, что существую динамические солитонные решения, которые в системе покоя испытывают периодические колебания. Такие решения называют бризерами (от английского breathe - дышать). Будем искать решение уравнения синус-Гордона () в виде

Подставляя в  , где индексы — соответствующие производные по
, где индексы — соответствующие производные по  и
и  , получаем:
, получаем:

|
(EQN)
|
В правой части первый член в круглых скобках зависит только от  , а второй — только от
, а второй — только от  . Поэтому беря производную по
. Поэтому беря производную по  , а затем по
, а затем по  мы от них избавляемся. В результате получается уравнение:
мы от них избавляемся. В результате получается уравнение:

Левая часть уравнения зависит только от времени, а правая только от координаты. Это возможно, если обе части уравнения равны некоторой константе. Обозначим её через  . В результате получаем два обыкновенных дифференциальных уравнений. Например, для
. В результате получаем два обыкновенных дифференциальных уравнений. Например, для  :
:

Умножая обе части на  и интегрируя, имеем:
и интегрируя, имеем:

где  — константа интегрирования. Умножая обе части на
— константа интегрирования. Умножая обе части на  и интегрируя еще раз, имеем (уравнение для
и интегрируя еще раз, имеем (уравнение для  выглядит также, но с заменой знака у
выглядит также, но с заменой знака у  и другими константами интегрирования
и другими константами интегрирования  и
и  ):
):

Разделение переменных (константа  ) мы провели для уравнения третьего порядка, тогда как исходное уравнение имеет второй порядок. Поэтому константы интегрирования не являются независимыми. Подставим найденные производные
) мы провели для уравнения третьего порядка, тогда как исходное уравнение имеет второй порядок. Поэтому константы интегрирования не являются независимыми. Подставим найденные производные  ,
,  ,
,  ,
,  в исходное уравнение (). Оно будет выполняться, если
в исходное уравнение (). Оно будет выполняться, если  и
и  . Поэтому:
. Поэтому:

|
(EQN)
|
Дальнейшее интегрирование приводит к эллиптическим интегралам.
Рассмотрим частные случаи. Если  ,
,  ,
,  имеем
имеем  и
и  , что приводит к решению в виде движущегося со скоростью
, что приводит к решению в виде движущегося со скоростью  кинка или антикинка ().
кинка или антикинка ().
Если  ,
,  ,
,  , после интегрирования, получаем \cite{PerringSkyrme1962}:
, после интегрирования, получаем \cite{PerringSkyrme1962}:

|
(EQN)
|
Это типичный бризер. Его амплитуда периодически изменяется со временем с частотой  . В отличие от кинка, поле бризера убывает на бесконечности в обе стороны от максимума. При этом максимум неподвижен, т.е. мы получили решение в системе покоя бризера. Так как уравнения ковариантны, всегда можно заставить бризер двигаться, подставив в решение преобразования Лоренца
. В отличие от кинка, поле бризера убывает на бесконечности в обе стороны от максимума. При этом максимум неподвижен, т.е. мы получили решение в системе покоя бризера. Так как уравнения ковариантны, всегда можно заставить бризер двигаться, подставив в решение преобразования Лоренца  и
и  .
.
Плотность энергии бизера равна:
![{\displaystyle W={\frac {8f^{2}g^{2}}{(f^{2}+g^{2})^{2}}}\left[{\frac {f_{t}^{2}}{f^{2}}}+{\frac {g_{x}^{2}}{g^{2}}}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d1b0206cd4b68452a42e154a09337d2b7e074f0)
и в случае решения () принимает вид:

где  и
и  . Ниже на рисунке приведены графики поля (слева) и плотности энергии (справа) бризера в различные моменты времени при
. Ниже на рисунке приведены графики поля (слева) и плотности энергии (справа) бризера в различные моменты времени при  :
:

Плотность энергии меняется со временем, однако полная энергия сохраняется, и масса бризера равна:

Таким образом, чем меньше частота колебаний бризера, тем больше будет его масса и тем уже и выше он будет.
Релятивистский мир - лекции по теории относительности, гравитации и космологии

































































































































![{\displaystyle W={\frac {8f^{2}g^{2}}{(f^{2}+g^{2})^{2}}}\left[{\frac {f_{t}^{2}}{f^{2}}}+{\frac {g_{x}^{2}}{g^{2}}}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d1b0206cd4b68452a42e154a09337d2b7e074f0)




