 Самой простой является группа циклических перестановок
Самой простой является группа циклических перестановок  элементов
элементов  . Пронумеруем углы правильного
. Пронумеруем углы правильного  -угольника. Пусть его вращают в плоскости на углы
-угольника. Пусть его вращают в плоскости на углы  , где
, где  без переворотов. Ниже представлены такие преобразования треугольника (
без переворотов. Ниже представлены такие преобразования треугольника ( ) и квадрата (
) и квадрата ( ):
):

Понятно, что это абелева группа. Поворот  раз на угол
раз на угол  порождает любой элемент группы. Для именования
порождает любой элемент группы. Для именования  элементов группы
элементов группы  удобно использовать следующие обозначения:
удобно использовать следующие обозначения: 

Имеется одна группа 2-го ( ) и одна 3-го порядка (
) и одна 3-го порядка ( ). Для 4-х элементов возможны две группы
). Для 4-х элементов возможны две группы  и
и  (см.выше). Для 5-ти — одна (
(см.выше). Для 5-ти — одна ( ).
).
Если правильному  -угольнику разрешено вращаться в плоскости вокруг центра симметрии, и переворачиваться вокруг осей симметрии, то получается группа диэдра
-угольнику разрешено вращаться в плоскости вокруг центра симметрии, и переворачиваться вокруг осей симметрии, то получается группа диэдра  порядка
порядка  . К
. К  относят и группу
относят и группу  преобразований прямоугольника (
преобразований прямоугольника ( \,H). Для треугольника (
\,H). Для треугольника ( ) имеем (для квадрата см.стр.\,\pageref{sym_D3_pic}):
) имеем (для квадрата см.стр.\,\pageref{sym_D3_pic}):

Кроме наименьшей неабелевой группы  для 6 элементов существует ещё абелева группа
для 6 элементов существует ещё абелева группа  . Группа 7-го порядка одна (
. Группа 7-го порядка одна ( ); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это
); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это  и группа кватернионов
и группа кватернионов  (см.стр.\,\pageref{quat_basis_def1}).
(см.стр.\,\pageref{quat_basis_def1}).
 В левом верхнем углу таблиц
В левом верхнем углу таблиц  находится блок, совпадающий с циклической группой. Говорят, что
находится блок, совпадающий с циклической группой. Говорят, что  является {подгруппой} группы
является {подгруппой} группы  .
.
Подгруппа  , это подмножество
, это подмножество  , элементов группы
, элементов группы  для которых выполняются все групповые свойства (есть единичный, у каждого элемента — обратный, и при умножении возникают только элементы из подгруппы
для которых выполняются все групповые свойства (есть единичный, у каждого элемента — обратный, и при умножении возникают только элементы из подгруппы  :
:  ). Так,
). Так,  .
.
Единичный элемент  и сама группа
и сама группа  являются подгруппами
являются подгруппами  . Их называют собственными. Выявление остальных (несобственных) подгрупп данной группы позволяет лучше понять её свойства.
. Их называют собственными. Выявление остальных (несобственных) подгрупп данной группы позволяет лучше понять её свойства.
Если  , а
, а  то
то  (отношение транзитивности). Для обозначения "вложенности" подгрупп иногда переворачивают значок подгруппы:
(отношение транзитивности). Для обозначения "вложенности" подгрупп иногда переворачивают значок подгруппы:  . Пересечение подгрупп также является подгруппой (иногда это только
. Пересечение подгрупп также является подгруппой (иногда это только  ). Стоит найти (
). Стоит найти ( \,H) подгруппы группы
\,H) подгруппы группы  и построить (
и построить ( \,H) иерархию подгрупп группы
\,H) иерархию подгрупп группы  .
.
 Если у группы
Если у группы  известна некоторая подгруппа
известна некоторая подгруппа  , то можно попытаться найти другие подгруппы. Для этого, выбирается фиксированный элемент
, то можно попытаться найти другие подгруппы. Для этого, выбирается фиксированный элемент  группы (
группы ( ), не принадлежащий
), не принадлежащий  (
( ) и строится сопряжённая подгруппа
) и строится сопряжённая подгруппа  , элементы которой получаются умножением всех элементов
, элементы которой получаются умножением всех элементов  слева на
слева на  , а справа на
, а справа на  . То, что такое множество элементов образует группу, легко проверяется (
. То, что такое множество элементов образует группу, легко проверяется ( \,H). Так, результат умножения остаётся внутри
\,H). Так, результат умножения остаётся внутри  :
:

Например, для  имеем
имеем  .
.
 Подгруппа
Подгруппа  называется инвариантной, если её сопряжение с любым элементом
называется инвариантной, если её сопряжение с любым элементом  снова дает
снова дает  (новая подгруппа не возникает). В этом случае для любого
(новая подгруппа не возникает). В этом случае для любого  имеем:
имеем:  или иначе
или иначе  . Заметим, что при сопряжении элемента
. Заметим, что при сопряжении элемента  получается вообще говоря другой элемент
получается вообще говоря другой элемент  инвариантной подгруппы. Несложно видеть, что все подгруппы абелевой группы являются инвариантными.
инвариантной подгруппы. Несложно видеть, что все подгруппы абелевой группы являются инвариантными.
Группа, не имеющая инвариантных подгрупп (кроме себя самой и единичного элемента) называется простой. Группа  не простая, так как
не простая, так как  инвариантна (
инвариантна ( \,H). Полупростой называется группа у которой все инвариантные подгруппы неабелевы.
\,H). Полупростой называется группа у которой все инвариантные подгруппы неабелевы.
Если  инвариантная подгруппа группы
инвариантная подгруппа группы  , а
, а  инвариантная подгруппа группы
инвариантная подгруппа группы  , то в общем случае
, то в общем случае  не является инвариантной подгруппой группы
не является инвариантной подгруппой группы  (хотя конечно
(хотя конечно  является подгруппой
является подгруппой  ). Т.е. инвариантность подгрупп не обладает транзитивностью.
). Т.е. инвариантность подгрупп не обладает транзитивностью.
 Циклическая группа </math>C_nНевозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , в отличие от групп диэдра }
D_n
Циклическая группа </math>C_nНевозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , в отличие от групп диэдра }
D_n n>3Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , является абелевой группой. Естественно это не единственный пример семейства абелевых групп. В циклической группе один производящий элемент генерит все остальные элементы группы. Однако производящих элементов может быть несколько. Рассмотрим, например, группу }
C_{n,m}$, задав её при помощи определяющих соотношений:
n>3Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , является абелевой группой. Естественно это не единственный пример семейства абелевых групп. В циклической группе один производящий элемент генерит все остальные элементы группы. Однако производящих элементов может быть несколько. Рассмотрим, например, группу }
C_{n,m}$, задав её при помощи определяющих соотношений:

Эта группа имеет порядок  и является абелевой, с двумя порождающими элементами. Например:
и является абелевой, с двумя порождающими элементами. Например:

Для наглядности, мы не стали вводить имена для двух новых элементов  и
и  , оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно главной диагонали (из левого верхнего угла в правый нижний).
, оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно главной диагонали (из левого верхнего угла в правый нижний).
Аналогично можно определить абелеву группу с тремя, и т.д. порождающими элементами. Они имеют наглядное представление в виде дисков открывающих замок в сейфе или камере хранения. Так, элементы группы  могут быть представлены при помощи следующих картинок (два диска замка нарисованы один в другом):
могут быть представлены при помощи следующих картинок (два диска замка нарисованы один в другом):

Вращение дисков независимы друг от друга, и это собственно и приводит к абелевости группы. Если мы имеем  дисков, с количеством цифр
дисков, с количеством цифр  ,...,
,..., , то порядок такой группы
, то порядок такой группы  будет равен
будет равен  . Любой элемент группы
. Любой элемент группы  раскладывается на коммутирующие множители порождающих элементов:
раскладывается на коммутирующие множители порождающих элементов:  , где
, где  .
.
Эти группы покрывают все возможные абелевы группы. Простые циклические группы являются их вырожденным случаем, когда порождающий элемент единственен или  — взаимопростые.
— взаимопростые.
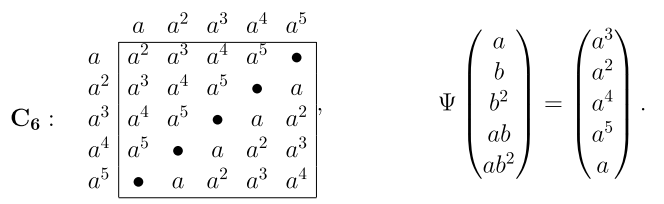
 Две группы называются изоморфными, если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы
Две группы называются изоморфными, если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы  и циклической группы
и циклической группы  (см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы
(см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы  к группе
к группе  :
:  и
и  (их 2-я и 3-я степени дают единичный элемент). Аналогично
(их 2-я и 3-я степени дают единичный элемент). Аналогично  , и т.д. В результате между элементами групп
, и т.д. В результате между элементами групп  и
и  устанавливается взаимооднозначное соответствие, сохраняющее групповое умножение, что обозначается следующим образом:
устанавливается взаимооднозначное соответствие, сохраняющее групповое умножение, что обозначается следующим образом:  . Это соответствие записано ниже справа в виде функции:
. Это соответствие записано ниже справа в виде функции:
Две группы  и
и  является гомоморфными если существует соответствие между их элементами, т.е. всюду определённая функция
является гомоморфными если существует соответствие между их элементами, т.е. всюду определённая функция  из
из  в
в  :
:  сохраняющая умножения:
сохраняющая умножения:  Множество
Множество  называется образом отображения:
называется образом отображения:  . Иногда пишут
. Иногда пишут  . Если функция
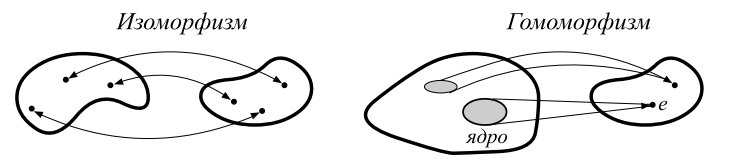
. Если функция  имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде:
имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде:
В качестве примера рассмотрим множество несингулярных (с ненулевыми определителями) матриц  x
x . Они имеют обратные, а, следовательно, их умножение удовлетворяет групповым аксиомам. Определитель произведения
. Они имеют обратные, а, следовательно, их умножение удовлетворяет групповым аксиомам. Определитель произведения  устанавливает гомоморфное отображение из группы матриц в группу ненулевых вещественных чисел.
устанавливает гомоморфное отображение из группы матриц в группу ненулевых вещественных чисел.
Множество элементов переходящих при гомоморфизме  в единичный элемент
в единичный элемент  называется ядром гомоморфизма и обозначается
называется ядром гомоморфизма и обозначается  . В примере с матрицами ядром является множество всех матриц с единичным определителем. Они образуют группу
. В примере с матрицами ядром является множество всех матриц с единичным определителем. Они образуют группу  .
.
Релятивистский мир - лекции по теории относительности, гравитации и космологии























































































