 Рассмотрим 3-мерное пространство с координатами
Рассмотрим 3-мерное пространство с координатами  . Группой вращения
. Группой вращения  называется линейное преобразование
называется линейное преобразование  , которое не изменяет длины радиус-вектора:
, которое не изменяет длины радиус-вектора:  (значок
(значок  — транспонирование):
— транспонирование):

где учтено, что при транспонировании произведения матриц их порядок меняется  . Чтобы квадрат вектора не изменился
. Чтобы квадрат вектора не изменился  , должно выполняться условие ортогональности:
, должно выполняться условие ортогональности:

Другими словами, обратная матрица к матрице поворота, является просто её транспонированием. Напомним, что буква " " в названии группы означает ортогональная, а тройка — размерность пространства.
" в названии группы означает ортогональная, а тройка — размерность пространства.
Так как определитель при транспонировании матрицы не изменяется, а определитель произведения матриц равен произведению их определителей, из условия ортогональности следует, что

Матрица вращения вокруг оси  (стр.\,\pageref{rotate_XY}) на угол
(стр.\,\pageref{rotate_XY}) на угол  имеет единичный определитель:
имеет единичный определитель:

Все матрицы вращения, имеющие единичный определитель образуют специальную ортогональную группу  .(3)$} Её также называют собственными преобразованиями или просто вращениями.
.(3)$} Её также называют собственными преобразованиями или просто вращениями.
Кроме вращений, длину радиус-вектора оставляют неизменными преобразования инверсии (или отражения осей):  . Матрица этого преобразования имеет вид:
. Матрица этого преобразования имеет вид:

Это тоже ортогональная матрица, но имеющая определитель равный минус единице:  , поэтому она принадлежит к группе
, поэтому она принадлежит к группе  , но не принадлежит к группе
, но не принадлежит к группе  .
.
Матрица  вместе с единичной матрицей
вместе с единичной матрицей  образует дискретную абелеву группу из двух элементов
образует дискретную абелеву группу из двух элементов  , изоморфную циклической группе
, изоморфную циклической группе  . При этом элемент группы
. При этом элемент группы  является обратным самому себе:
является обратным самому себе:  . Так как эта группа является "частным случаем" группы
. Так как эта группа является "частным случаем" группы  , то она является её подгруппой, т.е.
, то она является её подгруппой, т.е.  .
.
Можно рассмотреть дискретную абелеву группу ранга 4, в которой кроме единичной матрицы есть ещё три элемента:

Они осуществляют инверсии пар осей и имеют единичный детерминант. Эта группа является подгруппой не только  , но
, но  , так как инверсия двух осей в 3-мерном пространстве всегда может быть реализована поворотом системы координат.
, так как инверсия двух осей в 3-мерном пространстве всегда может быть реализована поворотом системы координат.
Подгруппой группы  является также более широкая группа инверсий, когда отражается одна, две или три оси. Инверсии осей
является также более широкая группа инверсий, когда отражается одна, две или три оси. Инверсии осей  ,
,  и
и  имеют следующее матричное представление:
имеют следующее матричное представление:

Стоит проверить что для  выполняется аксиома замкнутости, а каждый элемент является обратным самому себе. Эта группа включает в качестве подгруппы группу отражения всех трёх осей, что записывается в виде такой цепочки:
выполняется аксиома замкнутости, а каждый элемент является обратным самому себе. Эта группа включает в качестве подгруппы группу отражения всех трёх осей, что записывается в виде такой цепочки:  . Группа
. Группа  8-го порядка изоморфна абелевой группе
8-го порядка изоморфна абелевой группе  (стр.\,\pageref{sym_C_n_k_def}) с тремя порождающими элементами
(стр.\,\pageref{sym_C_n_k_def}) с тремя порождающими элементами  ,
,  и
и  второго порядка.
второго порядка.
Инвертирование сразу трёх осей (или одной) переводит правую систему координат в левую и наоборот. После такого инвертирования ни каким поворотом нельзя вернуться в исходное состояние. Таким образом, все преобразования группы  можно разбить на два класса — обычные вращения правой и левой системы координат. Это записывается в виде прямого произведения групп вращений и инверсий всех осей:
можно разбить на два класса — обычные вращения правой и левой системы координат. Это записывается в виде прямого произведения групп вращений и инверсий всех осей:

В данном случае прямое произведение означает, что рассматриваются последовательные преобразования  или
или  , т.е. пары матриц из групп
, т.е. пары матриц из групп  и
и  матрично перемножаются. Так как матрицы
матрично перемножаются. Так как матрицы  пропорциональны единичной, то
пропорциональны единичной, то  .
.
 Рассмотрим подробнее группу вращений
Рассмотрим подробнее группу вращений  . Введём матрицу
. Введём матрицу  небольшого отклонения от единичного преобразования (поворот на малые углы):
небольшого отклонения от единичного преобразования (поворот на малые углы):  . Пренебрегая вторым порядком малости, запишем условие ортогональности:
. Пренебрегая вторым порядком малости, запишем условие ортогональности:

Операция транспонирования переставляет местами индексы, следовательно матрица  является антисимметричной. Она имеет три независимых элемента:
является антисимметричной. Она имеет три независимых элемента:

|
(EQN)
|
Величины  можно рассматривать как малые параметры преобразования. Генераторы группы
можно рассматривать как малые параметры преобразования. Генераторы группы  имеют вид:
имеют вид:

|
(EQN)
|
Прямым перемножением матриц несложно проверить, что они удовлетворяют следующей алгебре Ли:
![{\displaystyle [{\mathbf {X} }_{1},\;{\mathbf {X} }_{2}]=-{\mathbf {X} }_{3},\;\;\;\;\;\;[{\mathbf {X} }_{3},\;{\mathbf {X} }_{1}]=-{\mathbf {X} }_{2},\;\;\;\;\;\;\;\;[{\mathbf {X} }_{2},\;{\mathbf {X} }_{3}]=-{\mathbf {X} }_{1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5ac551388b122b5652abace7eb25ce979707c71)
|
(EQN)
|
Поэтому структурные константы равны  . Второй и третий коммутаторы получаются из первого, в результате циклической перестановки индексов:
. Второй и третий коммутаторы получаются из первого, в результате циклической перестановки индексов:  . Стоит вычислить (
. Стоит вычислить ( \,H) эти коммутаторы операторным методом (стр.\,\pageref{sym_oper_method}).
\,H) эти коммутаторы операторным методом (стр.\,\pageref{sym_oper_method}).
Коммутаторы () можно записать используя символ Леви-Чевиты:
![{\displaystyle [{\mathbf {X} }_{i},\;{\mathbf {X} }_{j}]=-\varepsilon _{ijk}\,{\mathbf {X} }_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be6d6c717205fc16a882ddecf554f67cb96e446)
( , по
, по  сумма). Матрица инверсии трёх осей пропорциональна единичной, поэтому коммутирует с каждым генератором:
сумма). Матрица инверсии трёх осей пропорциональна единичной, поэтому коммутирует с каждым генератором: ![{\displaystyle \textstyle [\mathbf {X} _{i},\;\mathbf {I} _{xyz}]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a1e15dbe560967b69683816ac376b15ef3cfcca) Кроме этого диагональными являются квадраты матриц генераторов:
Кроме этого диагональными являются квадраты матриц генераторов:

откуда следует, что  , и т.д. Сумма квадратов генераторов
, и т.д. Сумма квадратов генераторов  пропорциональна единичной матрице, а следовательно коммутирует со всеми генераторами:
пропорциональна единичной матрице, а следовательно коммутирует со всеми генераторами: ![{\displaystyle \textstyle [{\mathbf {C} },{\mathbf {X} }_{i}]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f80ce191dd705dcb8dfce4460bd593482cc6d7b) Подобная величина в теории групп называется оператором Казимира.
Подобная величина в теории групп называется оператором Казимира.
Генераторы  ,
,  и
и  связаны с бесконечно малыми поворотами вокруг осей
связаны с бесконечно малыми поворотами вокруг осей  и
и  . Если обозначить
. Если обозначить  ,
,  и т.д., то повороты вокруг трёх осей будут иметь вид:
и т.д., то повороты вокруг трёх осей будут иметь вид:

Определители этих матриц равны 1, поэтому мы имеем дело с группой  . Разложение их по параметрам
. Разложение их по параметрам  приводит к генераторам
приводит к генераторам  .
.
Обратим внимание, что поворот в матрицах  ,
,  ,
,  происходит по правому винту (штопору) "вкручивающемуся" в направлении оси. Поэтому при повороте вокруг
происходит по правому винту (штопору) "вкручивающемуся" в направлении оси. Поэтому при повороте вокруг  роль "первой" оси (от которой отсчитывается угол) играет
роль "первой" оси (от которой отсчитывается угол) играет  , а "второй' —
, а "второй' —  :
:

В результате матрицы  и
и  "блочно" одинаковы, а в матрице
"блочно" одинаковы, а в матрице  по отношению к
по отношению к  переставлены местами строчки и аналогично колонки.
переставлены местами строчки и аналогично колонки.
Группа  является неабелевой и последовательность поворотов играет роль. Например, если сначала повернуть систему вокруг оси
является неабелевой и последовательность поворотов играет роль. Например, если сначала повернуть систему вокруг оси  , а затем вокруг оси
, а затем вокруг оси  , получим одну матрицу, а при выполнении этих поворотов в обратном порядке — другую:
, получим одну матрицу, а при выполнении этих поворотов в обратном порядке — другую:

Неабелевость группы вращений связана с ненулевыми структурными константами. Понятно, что если коммутатор бесконечно малых поворотов (генераторов) отличен от нуля, то и матрицы произвольного поворота не будут между собой коммутировать. Естественно в группе  можно выделить и абелевы подгруппы. Например, вращение вокруг одной оси на различные углы является абелевой группой
можно выделить и абелевы подгруппы. Например, вращение вокруг одной оси на различные углы является абелевой группой  .
.
Описание композиции вращений существенно упрощается при использовании кватернионной техники. Поэтому к группе  мы вернемся при рассмотрении соответствующей темы в главе . В частности, получим явное выражение для функции композиции
мы вернемся при рассмотрении соответствующей темы в главе . В частности, получим явное выражение для функции композиции  .
.
 Найдем выражение для матрицы поворота на угол
Найдем выражение для матрицы поворота на угол  вокруг произвольно направленного единичного вектора
вокруг произвольно направленного единичного вектора  . Пусть с твёрдым телом, вращающимся вокруг оси
. Пусть с твёрдым телом, вращающимся вокруг оси  (ниже первый рисунок) жёстко связан некоторый вектор
(ниже первый рисунок) жёстко связан некоторый вектор  . При повороте на угол
. При повороте на угол  он переходит в вектор
он переходит в вектор  , скользя по перевёрнутому конусу (второй рисунок):
, скользя по перевёрнутому конусу (второй рисунок):
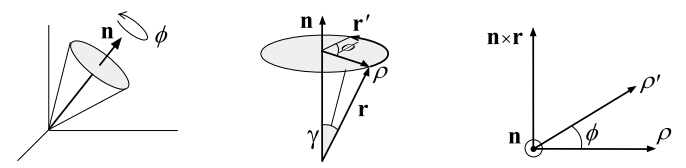
Обозначим проекцию  на основание конуса через
на основание конуса через  , а проекцию
, а проекцию  через
через  . Их длины одинаковы, и вектор
. Их длины одинаковы, и вектор  , в результате поворота на угол
, в результате поворота на угол  , переходит в
, переходит в  . Введём вектор
. Введём вектор  , лежащий в основании конуса перпендикулярно
, лежащий в основании конуса перпендикулярно  (см. "вид сверху" на третьем рисунке). Его длина равна
(см. "вид сверху" на третьем рисунке). Его длина равна  (второй рисунок), поэтому
(второй рисунок), поэтому  можно разложить по двум перпендикулярным векторам, имеющим одинаковую длину:
можно разложить по двум перпендикулярным векторам, имеющим одинаковую длину:
![{\displaystyle {\boldsymbol {\rho }}'={\boldsymbol {\rho }}\cos \phi +[\mathbf {n} \times \mathbf {r} ]\sin \phi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c25a4860f08ccb10aef5ba7f4698d0160aa8457a)
С другой стороны, векторы  и
и  можно разложить следующим образом:
можно разложить следующим образом:

|
(EQN)
|
где  направлен вдоль
направлен вдоль  и равен высоте конуса. В результате, учитывая, что
и равен высоте конуса. В результате, учитывая, что  , получаем:
, получаем: ![{\displaystyle \textstyle \mathbf {r} '={\boldsymbol {\rho }}\cos \phi +[\mathbf {n} \times \mathbf {r} ]\sin \phi +\mathbf {n} \;(\mathbf {n} \,\mathbf {r} ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6732001058e31a109294bdc60bfd6787e8f41c27)
Принято различать пассивные и активные повороты. В первом случае сравниваются координаты одной и той же фиксированной точки пространства в двух системах координат  и
и  , повёрнутых относительно друг друга на угол
, повёрнутых относительно друг друга на угол  . При активных вращениях рассматриваются координаты некоторого вектора, после его поворота относительно одной и той же системы координат:
. При активных вращениях рассматриваются координаты некоторого вектора, после его поворота относительно одной и той же системы координат:

Преобразования Лоренца описывают одно и тоже событие из различных систем отчёта, поэтому они являются пассивными вращениями. Для пространственных вращений мы также будем использовать пассивную интерпретацию. Несложно видеть, что поворот тела на угол  относительно неподвижной системы координат эквивалентно повороту системы координат при неподвижном теле на угол "
относительно неподвижной системы координат эквивалентно повороту системы координат при неподвижном теле на угол " ".
".
Поэтому, делая замену  и меняя порядок векторов в векторном произведении, а также выражая
и меняя порядок векторов в векторном произведении, а также выражая  через
через  при помощи первого соотношения (), окончательно, получаем:
при помощи первого соотношения (), окончательно, получаем:
![{\displaystyle \mathbf {r} '=\mathbf {r} \,\cos \phi +\mathbf {n} (\mathbf {n} \mathbf {r} )(1-\cos \phi )-[\mathbf {n} \times \mathbf {r} ]\sin \phi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee61f74fa1f7a248a61e038a390473627792ebf)
|
(EQN)
|
Пусть ось вращения направлена вдоль оси  . Тогда компоненты единичного вектора имеют значения
. Тогда компоненты единичного вектора имеют значения  . Записывая
. Записывая  и аналогично со штрихами, из () получаем преобразование (), стр.\,\pageref{rotate_XY} для вращения в плоскости
и аналогично со штрихами, из () получаем преобразование (), стр.\,\pageref{rotate_XY} для вращения в плоскости  :
:

Напомним, что при описании вращения используется правило правого винта (штопора). Этот винт вкручивается на угол  в направлении оси
в направлении оси  и его поворот показывает направление вращения системы координат. Кроме этого различают правые и левые системы координат:
и его поворот показывает направление вращения системы координат. Кроме этого различают правые и левые системы координат:
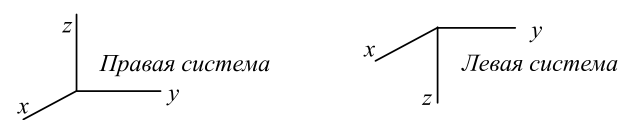
В книге используется правая система. В этой системе ось  получается при помощи того же правого винта, если его рукоятку поворачивать от оси
получается при помощи того же правого винта, если его рукоятку поворачивать от оси  к оси
к оси  в направлении
в направлении  . В 3-мерном пространстве левая система координат получается из правой в результате инверсии (обращении) одной или трёх осей. После такой операции, ни каким поворотом нельзя совместить оси левой и правой систем координат.
. В 3-мерном пространстве левая система координат получается из правой в результате инверсии (обращении) одной или трёх осей. После такой операции, ни каким поворотом нельзя совместить оси левой и правой систем координат.
Векторное соотношение () можно записать в тензорном виде для преобразования  , при помощи символа Кронекера
, при помощи символа Кронекера  и антисимметричного тензора Леви-Чевиты (
и антисимметричного тензора Леви-Чевиты (![{\displaystyle \textstyle [\mathbf {n} \times \mathbf {r} ]_{i}=\varepsilon _{ikj}n_{k}r_{j}=-\varepsilon _{ijk}n_{k}r_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186b0432471fa7b8de91095322053045f4f30bdb) ):
):

|
(EQN)
|
Для бесконечно малого по углу  преобразования, раскладывая в ряд синус и косинус, имеем
преобразования, раскладывая в ряд синус и косинус, имеем  , Поэтому генераторы группы равны
, Поэтому генераторы группы равны  , где индекс
, где индекс  перечисляет матрицы генераторов, а
перечисляет матрицы генераторов, а  — их элементы. Символ Леви-Чевиты равен
— их элементы. Символ Леви-Чевиты равен  , при перестановке двух индексов появляется минус и при совпадении любых индексов он равен нулю. Поэтому несложно проверить, что значения
, при перестановке двух индексов появляется минус и при совпадении любых индексов он равен нулю. Поэтому несложно проверить, что значения  совпадают с элементами матриц ().
совпадают с элементами матриц ().
 Из геометрических соображений понятно, что вращения вокруг различных единичных осей на некоторые углы охватывают все возможные вращения. Два последовательных вращения вокруг осей
Из геометрических соображений понятно, что вращения вокруг различных единичных осей на некоторые углы охватывают все возможные вращения. Два последовательных вращения вокруг осей  и
и  на углы
на углы  и
и  всегда можно выразить через один поворот на угол
всегда можно выразить через один поворот на угол  вокруг единичного вектора
вокруг единичного вектора  . Связь между параметрами исходных поворотов и их результата будет получена в главе . Сейчас рассмотрим два последовательных поворота вокруг одной и той же оси. В этом случае происходит обычное сложение углов поворота (если последовательные вращения происходят вокруг разных осей это не так!):
. Связь между параметрами исходных поворотов и их результата будет получена в главе . Сейчас рассмотрим два последовательных поворота вокруг одной и той же оси. В этом случае происходит обычное сложение углов поворота (если последовательные вращения происходят вокруг разных осей это не так!):

Возьмем производную по  , приравняв
, приравняв  , а
, а  :
:

|
(EQN)
|
где матрицу  , при помощи выражения (), можно выразить через генераторы группы:
, при помощи выражения (), можно выразить через генераторы группы:

Так как последовательность поворотов вокруг одной оси не играет роли ( ), матрицы
), матрицы  и
и  коммутируют (перестановочны). Следовательно, решение дифференциального матричного уравнения () можно записать следующим образом:
коммутируют (перестановочны). Следовательно, решение дифференциального матричного уравнения () можно записать следующим образом:

|
(EQN)
|
Экспонента от матрицы понимается в смысле её разложения в бесконечный степенной ряд Тейлора (возведение в произвольную степень матрицы является хорошо определенной операцией). Предполагается, что каждый элемент матрицы, получившейся в результате такого суммирования сходится к определенному значению. Стоит, разложив экспоненту, с точностью до второго порядка малости по  , убедиться, что с той же точностью воспроизводится выражение (). Для этого сначала необходимо найти при помощи () следующие матрицы:
, убедиться, что с той же точностью воспроизводится выражение (). Для этого сначала необходимо найти при помощи () следующие матрицы:

где учтено, что  . Обратим внимание, что
. Обратим внимание, что  является симметричной матрицей (как и квадрат любой антисимметричной матрицы
является симметричной матрицей (как и квадрат любой антисимметричной матрицы  ).
).
 Аналогичное экспоненциальное представление c генераторами группы в показателе справедливо для многих линейных групп Ли. Остановимся на этом чуть подробнее. Пусть в групповом пространстве задана некоторая кривая. Это означает, что из всех элементов группы отобраны только такие элементы
Аналогичное экспоненциальное представление c генераторами группы в показателе справедливо для многих линейных групп Ли. Остановимся на этом чуть подробнее. Пусть в групповом пространстве задана некоторая кривая. Это означает, что из всех элементов группы отобраны только такие элементы  , которые можно перечислить (пронумеровать) при помощи одного непрерывного параметра
, которые можно перечислить (пронумеровать) при помощи одного непрерывного параметра  . Считается, что элементы группы на кривой близки, если близки соответствующие им параметры. В случае матричных групп, элементы двух близких матриц близки в обычном смысле математического анализа. Для многопараметрических групп подмножество элементов, заданных на кривой не охватывает всех элементов группы. Однако, для ряда интересных в приложениях линейных групп множество всевозможных кривых, проходящих через единичный элемент
. Считается, что элементы группы на кривой близки, если близки соответствующие им параметры. В случае матричных групп, элементы двух близких матриц близки в обычном смысле математического анализа. Для многопараметрических групп подмножество элементов, заданных на кривой не охватывает всех элементов группы. Однако, для ряда интересных в приложениях линейных групп множество всевозможных кривых, проходящих через единичный элемент  (для которого естественно положить
(для которого естественно положить  ), покрывают все групповое пространство, пересекаясь только в единичном элементе. Более того, произведение двух элементов группы, лежащих на кривой, даёт элемент, который лежит на этой же кривой. Поэтому, всегда можно выбрать параметризацию, для которой:
), покрывают все групповое пространство, пересекаясь только в единичном элементе. Более того, произведение двух элементов группы, лежащих на кривой, даёт элемент, который лежит на этой же кривой. Поэтому, всегда можно выбрать параметризацию, для которой:

Продифференцируем это выражение по  , положив его равным нулю, а
, положив его равным нулю, а  :
:

Так как в окрестности единичного преобразования матрицу  можно разложить по генераторам группы, то
можно разложить по генераторам группы, то

где  — коэффициенты разложения и число слагаемых в сумме по
— коэффициенты разложения и число слагаемых в сумме по  равно числу параметров группы. Аналогичное уравнение, с переставленными матрицами
равно числу параметров группы. Аналогичное уравнение, с переставленными матрицами  и
и  мы бы получили, продифференцировав по
мы бы получили, продифференцировав по  . Поэтому они коммутируют и решение уравнения можно записать в виде:
. Поэтому они коммутируют и решение уравнения можно записать в виде:

Числа  имеют смысл компонент касательного к кривой вектора в групповом пространстве в окрестности единичного преобразования, который разложен по базису генераторов
имеют смысл компонент касательного к кривой вектора в групповом пространстве в окрестности единичного преобразования, который разложен по базису генераторов  . Масштабным преобразованием параметра
. Масштабным преобразованием параметра  всегда можно сделать сумму квадратов коэффициентов
всегда можно сделать сумму квадратов коэффициентов  равной единице.
равной единице.
Релятивистский мир - лекции по теории относительности, гравитации и космологии






















































![{\displaystyle [{\mathbf {X} }_{1},\;{\mathbf {X} }_{2}]=-{\mathbf {X} }_{3},\;\;\;\;\;\;[{\mathbf {X} }_{3},\;{\mathbf {X} }_{1}]=-{\mathbf {X} }_{2},\;\;\;\;\;\;\;\;[{\mathbf {X} }_{2},\;{\mathbf {X} }_{3}]=-{\mathbf {X} }_{1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5ac551388b122b5652abace7eb25ce979707c71)



![{\displaystyle [{\mathbf {X} }_{i},\;{\mathbf {X} }_{j}]=-\varepsilon _{ijk}\,{\mathbf {X} }_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be6d6c717205fc16a882ddecf554f67cb96e446)


![{\displaystyle \textstyle [\mathbf {X} _{i},\;\mathbf {I} _{xyz}]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a1e15dbe560967b69683816ac376b15ef3cfcca)



![{\displaystyle \textstyle [{\mathbf {C} },{\mathbf {X} }_{i}]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f80ce191dd705dcb8dfce4460bd593482cc6d7b)






















![{\displaystyle {\boldsymbol {\rho }}'={\boldsymbol {\rho }}\cos \phi +[\mathbf {n} \times \mathbf {r} ]\sin \phi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c25a4860f08ccb10aef5ba7f4698d0160aa8457a)



![{\displaystyle \textstyle \mathbf {r} '={\boldsymbol {\rho }}\cos \phi +[\mathbf {n} \times \mathbf {r} ]\sin \phi +\mathbf {n} \;(\mathbf {n} \,\mathbf {r} ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6732001058e31a109294bdc60bfd6787e8f41c27)




![{\displaystyle \mathbf {r} '=\mathbf {r} \,\cos \phi +\mathbf {n} (\mathbf {n} \mathbf {r} )(1-\cos \phi )-[\mathbf {n} \times \mathbf {r} ]\sin \phi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee61f74fa1f7a248a61e038a390473627792ebf)






![{\displaystyle \textstyle [\mathbf {n} \times \mathbf {r} ]_{i}=\varepsilon _{ikj}n_{k}r_{j}=-\varepsilon _{ijk}n_{k}r_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186b0432471fa7b8de91095322053045f4f30bdb)




































