Примеры и определения

Что такое симметрия? <<	Оглавление (Последняя версия в: Глава 5)	>> Группа перестановок

---

$\textstyle \bullet$ Самой простой является группа циклических перестановок $\textstyle n$ элементов $\textstyle \mathbf {C_{n}}$. Пронумеруем углы правильного $\textstyle n$-угольника. Пусть его вращают в плоскости на углы $\textstyle 2\pi m/n$, где $\textstyle m=0,...,n-1$ без переворотов. Ниже представлены такие преобразования треугольника ($\textstyle \mathbf {C_{3}}$) и квадрата ($\textstyle \mathbf {C_{4}}$):

Понятно, что это абелева группа. Поворот $\textstyle m$ раз на угол $\textstyle a:\;2\pi /n$ порождает любой элемент группы. Для именования $\textstyle n$ элементов группы $\textstyle \mathbf {C_{n}}$ удобно использовать следующие обозначения: $\textstyle \mathbf {C_{n}} =\{e,a,a^{2},a^{3},...,a^{n-1}\}:$

Имеется одна группа 2-го ($\textstyle \mathbf {C} _{2}$) и одна 3-го порядка ($\textstyle \mathbf {C} _{3}$). Для 4-х элементов возможны две группы $\textstyle \mathbf {C} _{4}$ и $\textstyle \mathbf {D} _{2}$ (см.выше). Для 5-ти — одна ($\textstyle \mathbf {C} _{5}$).

Если правильному $\textstyle n$-угольнику разрешено вращаться в плоскости вокруг центра симметрии, и переворачиваться вокруг осей симметрии, то получается группа диэдра $\textstyle \mathbf {D_{n}} =\left\langle a,b|a^{n}=e,\;b^{2}=e,\;(ab)^{2}=e\right\rangle$ порядка $\textstyle 2n$. К $\textstyle \mathbf {D_{n}}$ относят и группу $\textstyle \mathbf {D} _{2}$ преобразований прямоугольника ($\textstyle \lessdot$\,H). Для треугольника ($\textstyle \mathbf {D_{3}}$) имеем (для квадрата см.стр.\,\pageref{sym_D3_pic}):

Кроме наименьшей неабелевой группы $\textstyle \mathbf {D_{3}}$ для 6 элементов существует ещё абелева группа $\textstyle \mathbf {C_{6}}$. Группа 7-го порядка одна ($\textstyle \mathbf {C_{7}}$); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это $\textstyle \mathbf {D_{4}}$ и группа кватернионов $\textstyle \mathbf {Q}$ (см.стр.\,\pageref{quat_basis_def1}).

$\textstyle \bullet$ В левом верхнем углу таблиц $\textstyle \mathbf {D_{n}}$ находится блок, совпадающий с циклической группой. Говорят, что $\textstyle \mathbf {C_{n}}$ является {подгруппой} группы $\textstyle \mathbf {D_{n}}$.

Подгруппа $\textstyle \mathbf {H}$, это подмножество $\textstyle \mathbf {H} \subset \mathbf {G}$, элементов группы $\textstyle \mathbf {G}$ для которых выполняются все групповые свойства (есть единичный, у каждого элемента — обратный, и при умножении возникают только элементы из подгруппы $\textstyle \mathbf {H}$: $\textstyle h_{i},\;h_{j},\;h_{i}\,h_{j}\in \mathbf {H}$). Так, $\textstyle {\mathbf {C} }_{3}\subset {\mathbf {D} }_{3}$.

Единичный элемент $\textstyle \{e\}$ и сама группа $\textstyle \mathbf {G}$ являются подгруппами $\textstyle \mathbf {G}$. Их называют собственными. Выявление остальных (несобственных) подгрупп данной группы позволяет лучше понять её свойства.

Если $\textstyle \mathbf {F} \subset \mathbf {H}$, а $\textstyle \mathbf {H} \subset \mathbf {G}$ то $\textstyle \mathbf {F} \subset \mathbf {G}$ (отношение транзитивности). Для обозначения "вложенности" подгрупп иногда переворачивают значок подгруппы: $\textstyle \mathbf {D_{4}} \supset \mathbf {C_{4}} \supset \mathbf {C_{2}}$. Пересечение подгрупп также является подгруппой (иногда это только $\textstyle \{e\}$). Стоит найти ($\textstyle \lessdot$\,H) подгруппы группы $\textstyle \mathbf {D_{3}}$ и построить ($\textstyle \lessdot$\,H) иерархию подгрупп группы $\textstyle \mathbf {D_{4}}$.

$\textstyle \bullet$ Если у группы $\textstyle \mathbf {G}$ известна некоторая подгруппа $\textstyle \mathbf {H}$, то можно попытаться найти другие подгруппы. Для этого, выбирается фиксированный элемент $\textstyle g$ группы ($\textstyle g\in \mathbf {G}$), не принадлежащий $\textstyle \mathbf {H}$ ($\textstyle g\not \in \mathbf {H}$) и строится сопряжённая подгруппа $\textstyle \mathbf {H} '=g\mathbf {H} g^{-1}$, элементы которой получаются умножением всех элементов $\textstyle \mathbf {H}$ слева на $\textstyle g$, а справа на $\textstyle g^{-1}$. То, что такое множество элементов образует группу, легко проверяется ($\textstyle \lessdot$\,H). Так, результат умножения остаётся внутри $\textstyle \mathbf {H} '$:

$h'_{i}h'_{j}=(g\,h_{i}\,g^{-1})\cdot (g\,h_{j}\,g^{-1})=g\,(h_{i}\,h_{j})\,g^{-1}=gh_{k}g^{-1}=h'_{k}\in \mathbf {H} '.$

Например, для $\textstyle \{e,b\}\subset \mathbf {D_{3}}$ имеем $\textstyle a\cdot \{e,b\}\cdot a^{-1}=\{a,c\}\cdot a^{2}=\{e,d\}\subset \mathbf {D_{3}}$.

$\textstyle \bullet$ Подгруппа $\textstyle \mathbf {H} \subset \mathbf {G}$ называется инвариантной, если её сопряжение с любым элементом $\textstyle \mathbf {G}$ снова дает $\textstyle \mathbf {H}$ (новая подгруппа не возникает). В этом случае для любого $\textstyle g\in \mathbf {G}$ имеем: $\textstyle g^{-1}\,h_{i}\,g=h_{j}\in \mathbf {H}$ или иначе $\textstyle h_{i}\,g=g\,h_{j}$. Заметим, что при сопряжении элемента $\textstyle h_{i}$ получается вообще говоря другой элемент $\textstyle h_{j}$ инвариантной подгруппы. Несложно видеть, что все подгруппы абелевой группы являются инвариантными.

Группа, не имеющая инвариантных подгрупп (кроме себя самой и единичного элемента) называется простой. Группа $\textstyle \mathbf {D} _{3}$ не простая, так как $\textstyle \mathbf {C} _{3}\subset \mathbf {D} _{3}$ инвариантна ($\textstyle \lessdot$\,H). Полупростой называется группа у которой все инвариантные подгруппы неабелевы.

Если $\textstyle \mathbf {H} _{1}$ инвариантная подгруппа группы $\textstyle \mathbf {G} \supset \mathbf {H} _{1}$, а $\textstyle \mathbf {H} _{2}$ инвариантная подгруппа группы $\textstyle \mathbf {H} _{1}\supset \mathbf {H} _{2}$, то в общем случае $\textstyle \mathbf {H} _{2}$ не является инвариантной подгруппой группы $\textstyle \mathbf {G}$ (хотя конечно $\textstyle \mathbf {H} _{2}$ является подгруппой $\textstyle \mathbf {G}$). Т.е. инвариантность подгрупп не обладает транзитивностью.

}Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle } } \bulletНевозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle Циклическая группа } C_nНевозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \textstyle , в отличие от групп диэдра } D_n$\textstyle ,$n>3Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , является абелевой группой. Естественно это не единственный пример семейства абелевых групп. В циклической группе один производящий элемент генерит все остальные элементы группы. Однако производящих элементов может быть несколько. Рассмотрим, например, группу } C_{n,m}$, задав её при помощи определяющих соотношений:

$\mathbf {C_{n,m}} =\left\langle a,b|\;a^{n}=e,\;\;b^{m}=e,\;\;ab=ba\;\right\rangle .$

Эта группа имеет порядок $\textstyle n\cdot m$ и является абелевой, с двумя порождающими элементами. Например:

Невозможно разобрать выражение (неизвестная функция «\multicolumn»): {\displaystyle \begin{array}{rl|c|cc|cc|} \multicolumn{2}{c}{} & \multicolumn{1}{c}{a} & \multicolumn{1}{c}{b} & \multicolumn{1}{c}{b^2}& \multicolumn{1}{c}{ab}& \multicolumn{1}{c}{ab^2}\\ \cline{3-7} & a & \bullet & ab & ab^2 & b & b^2 \\ \cline{3-7} & b & ab & b^2 & \bullet & ab^2 & a \\ \mathbf{C_{2,3}}:\;\;& b^2 & ab^2 & \bullet & b & a & ab \\ \cline{3-7} & ab & b & ab^2 & a & b^2 & \bullet \\ & ab^2& b^2 & a & ab & \bullet & b \\ \cline{3-7} \end{array}}

Для наглядности, мы не стали вводить имена для двух новых элементов $\textstyle c=ab$ и $\textstyle d=ab^{2}$, оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно главной диагонали (из левого верхнего угла в правый нижний).

Аналогично можно определить абелеву группу с тремя, и т.д. порождающими элементами. Они имеют наглядное представление в виде дисков открывающих замок в сейфе или камере хранения. Так, элементы группы $\textstyle \mathbf {C_{2,3}}$ могут быть представлены при помощи следующих картинок (два диска замка нарисованы один в другом):

Вращение дисков независимы друг от друга, и это собственно и приводит к абелевости группы. Если мы имеем $\textstyle n$ дисков, с количеством цифр $\textstyle k_{1}$,...,$\textstyle k_{n}$, то порядок такой группы $\textstyle \mathbf {C_{k_{1}...k_{n}}}$ будет равен $\textstyle k_{1}\cdot ...\cdot k_{n}$. Любой элемент группы $\textstyle \mathbf {C} _{\mathbf {k} _{1}...k_{n}}$ раскладывается на коммутирующие множители порождающих элементов: $\textstyle a_{1}^{m_{1}}\cdot ...a_{n}^{m_{n}}$, где $\textstyle m_{i}<k_{i}$.

Эти группы покрывают все возможные абелевы группы. Простые циклические группы являются их вырожденным случаем, когда порождающий элемент единственен или $\textstyle k_{i}$ — взаимопростые.

$\textstyle \bullet$ Две группы называются изоморфными, если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы $\textstyle \mathbf {C_{2,3}}$ и циклической группы $\textstyle \mathbf {C_{6}}$ (см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы $\textstyle \mathbf {C_{2,3}}$ к группе $\textstyle \mathbf {C_{6}}$: $\textstyle a\mapsto a^{3}$ и $\textstyle b\mapsto a^{2}$ (их 2-я и 3-я степени дают единичный элемент). Аналогично $\textstyle ab\mapsto a^{3}\cdot a^{2}=a^{5}$, и т.д. В результате между элементами групп $\textstyle \mathbf {C_{2,3}}$ и $\textstyle \mathbf {C_{6}}$ устанавливается взаимооднозначное соответствие, сохраняющее групповое умножение, что обозначается следующим образом: $\textstyle \mathbf {C_{2,3}} \approx \mathbf {C_{6}}$. Это соответствие записано ниже справа в виде функции:

Невозможно разобрать выражение (неизвестная функция «\multicolumn»): {\displaystyle \begin{array}{rl|ccccc|} \multicolumn{2}{c}{} & \multicolumn{1}{c}{a} & \multicolumn{1}{c}{a^2} & \multicolumn{1}{c}{a^3}& \multicolumn{1}{c}{a^4}& \multicolumn{1}{c}{a^5}\\ \cline{3-7} & a & a^2 & a^3 & a^4 & a^5 & \bullet \\ & a^2 & a^3 & a^4 & a^5 & \bullet & a \\ \mathbf{C_{6}}:\;\; & a^3 & a^4 & a^5 & \bullet & a & a^2 \\ & a^4 & a^5 &\bullet & a & a^2 & a^3 \\ & a^5 & \bullet & a & a^2 & a^3 & a^4 \\ \cline{3-7} \end{array}, \;\;\;\;\;\;\;\;\;\;\;\;\;\; \Psi \begin{pmatrix} a \\ b \\ b^2 \\ ab \\ ab^2 \\ \end{pmatrix}= \begin{pmatrix} a^3 \\ a^2 \\ a^4 \\ a^5 \\ a \\ \end{pmatrix}.}

Две группы $\textstyle \mathbf {G}$ и $\textstyle \mathbf {G} '$ является гомоморфными если существует соответствие между их элементами, т.е. всюду определённая функция $\textstyle \Psi$ из $\textstyle \mathbf {G}$ в $\textstyle \mathbf {G} '$: $\textstyle g_{k}'=\Psi (g_{i})$ сохраняющая умножения: $\textstyle \Psi (g_{i}\,g_{j})=\Psi (g_{i})\Psi (g_{j}).$ Множество $\textstyle \mathbf {G} '$ называется образом отображения: $\textstyle \mathbf {G} '=\Psi (\mathbf {G} )$. Иногда пишут $\textstyle \mathbf {G} '={\rm {Im}}\,\Psi$. Если функция $\textstyle \Psi$ имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде:

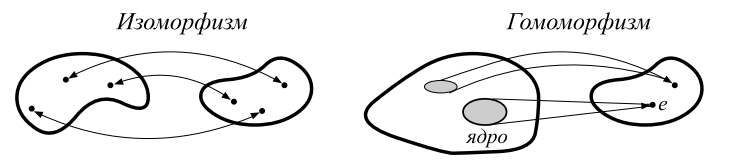
В качестве примера рассмотрим множество несингулярных (с ненулевыми определителями) матриц $\textstyle n$x$\textstyle n$. Они имеют обратные, а, следовательно, их умножение удовлетворяет групповым аксиомам. Определитель произведения $\textstyle \det(\mathbf {A} \mathbf {B} )=\det \mathbf {A} \det \mathbf {B}$ устанавливает гомоморфное отображение из группы матриц в группу ненулевых вещественных чисел.

Множество элементов переходящих при гомоморфизме $\textstyle \mathbf {G} '=\Psi (\mathbf {G} )$ в единичный элемент $\textstyle e'\in \mathbf {G} '$ называется ядром гомоморфизма и обозначается $\textstyle {\rm {ker}}\,\Psi$. В примере с матрицами ядром является множество всех матриц с единичным определителем. Они образуют группу $\textstyle \mathbf {SL} (n,C)$.

---

Что такое симметрия? <<	Оглавление (Последняя версия в: Глава 5)	>> Группа перестановок

---

Релятивистский мир - лекции по теории относительности, гравитации и космологии