Примеры и определения — различия между версиями
WikiSysop (обсуждение | вклад) |
WikiSysop (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
{| width="100%" | {| width="100%" | ||
| width="30%"|[[Что такое симметрия?]] << | | width="30%"|[[Что такое симметрия?]] << | ||
| − | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/ | + | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/relworld_06.pdf Глава 6]) |
| width="30%" align="right"| >> [[Группа перестановок]] | | width="30%" align="right"| >> [[Группа перестановок]] | ||
|} | |} | ||
| Строка 12: | Строка 12: | ||
Понятно, что это абелева группа. Поворот <math>\textstyle m</math> раз на угол <math>\textstyle a:\;2\pi/n</math> ''порождает'' любой элемент группы. Для именования <math>\textstyle n</math> элементов группы <math>\textstyle \mathbf{C_n}</math> удобно использовать следующие обозначения: <math>\textstyle \mathbf{C_n} = \{e, a, a^2, a^3, ..., a^{n-1}\}:</math> | Понятно, что это абелева группа. Поворот <math>\textstyle m</math> раз на угол <math>\textstyle a:\;2\pi/n</math> ''порождает'' любой элемент группы. Для именования <math>\textstyle n</math> элементов группы <math>\textstyle \mathbf{C_n}</math> удобно использовать следующие обозначения: <math>\textstyle \mathbf{C_n} = \{e, a, a^2, a^3, ..., a^{n-1}\}:</math> | ||
| − | + | <center>[[File:sym_tbl03.png]]</center> | |
Имеется одна группа 2-го (<math>\textstyle \mathbf{C}_2</math>) и одна 3-го порядка (<math>\textstyle \mathbf{C}_3</math>). Для 4-х элементов возможны две группы <math>\textstyle \mathbf{C}_4</math> и <math>\textstyle \mathbf{D}_2</math> (см.выше). Для 5-ти — одна (<math>\textstyle \mathbf{C}_5</math>). | Имеется одна группа 2-го (<math>\textstyle \mathbf{C}_2</math>) и одна 3-го порядка (<math>\textstyle \mathbf{C}_3</math>). Для 4-х элементов возможны две группы <math>\textstyle \mathbf{C}_4</math> и <math>\textstyle \mathbf{D}_2</math> (см.выше). Для 5-ти — одна (<math>\textstyle \mathbf{C}_5</math>). | ||
| Строка 19: | Строка 19: | ||
<center>[[File:group_D3.png]]</center> | <center>[[File:group_D3.png]]</center> | ||
| − | |||
| − | |||
Кроме наименьшей неабелевой группы <math>\textstyle \mathbf{D_3}</math> для 6 элементов существует ещё абелева группа <math>\textstyle \mathbf{C_6}</math>. Группа 7-го порядка одна (<math>\textstyle \mathbf{C_7}</math>); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это <math>\textstyle \mathbf{D_4}</math> и группа кватернионов <math>\textstyle \mathbf{Q}</math> (см.стр.\,\pageref{quat_basis_def1}). | Кроме наименьшей неабелевой группы <math>\textstyle \mathbf{D_3}</math> для 6 элементов существует ещё абелева группа <math>\textstyle \mathbf{C_6}</math>. Группа 7-го порядка одна (<math>\textstyle \mathbf{C_7}</math>); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это <math>\textstyle \mathbf{D_4}</math> и группа кватернионов <math>\textstyle \mathbf{Q}</math> (см.стр.\,\pageref{quat_basis_def1}). | ||
| Строка 44: | Строка 42: | ||
Если <math>\textstyle \mathbf{H}_1</math> инвариантная подгруппа группы <math>\textstyle \mathbf{G} \supset \mathbf{H}_1</math>, а <math>\textstyle \mathbf{H}_2</math> инвариантная подгруппа группы <math>\textstyle \mathbf{H}_1\supset \mathbf{H}_2</math>, то в общем случае <math>\textstyle \mathbf{H}_2</math> не является инвариантной подгруппой группы <math>\textstyle \mathbf{G}</math> (хотя конечно <math>\textstyle \mathbf{H}_2</math> является подгруппой <math>\textstyle \mathbf{G}</math>). Т.е. инвариантность подгрупп не обладает транзитивностью. | Если <math>\textstyle \mathbf{H}_1</math> инвариантная подгруппа группы <math>\textstyle \mathbf{G} \supset \mathbf{H}_1</math>, а <math>\textstyle \mathbf{H}_2</math> инвариантная подгруппа группы <math>\textstyle \mathbf{H}_1\supset \mathbf{H}_2</math>, то в общем случае <math>\textstyle \mathbf{H}_2</math> не является инвариантной подгруппой группы <math>\textstyle \mathbf{G}</math> (хотя конечно <math>\textstyle \mathbf{H}_2</math> является подгруппой <math>\textstyle \mathbf{G}</math>). Т.е. инвариантность подгрупп не обладает транзитивностью. | ||
| − | + | <math>\bullet</math> Циклическая группа </math>'''C_n'''<math>\textstyle , в отличие от групп диэдра </math>'''D_n'''<math>\textstyle , </math>n>3<math>\textstyle , является абелевой группой. Естественно это не единственный пример семейства абелевых групп. В циклической группе один производящий элемент генерит все остальные элементы группы. Однако производящих элементов может быть несколько. Рассмотрим, например, группу </math>'''C_{n,m'''}$, задав её при помощи определяющих соотношений: | |
:<center><math>\mathbf{C_{n,m}} = \left\langle a, b| \;a^n=e,\;\;b^m=e,\;\;ab=ba\;\right\rangle .</math></center> | :<center><math>\mathbf{C_{n,m}} = \left\langle a, b| \;a^n=e,\;\;b^m=e,\;\;ab=ba\;\right\rangle .</math></center> | ||
| Строка 50: | Строка 48: | ||
Эта группа имеет порядок <math>\textstyle n\cdot m</math> и является абелевой, с двумя порождающими элементами. Например: | Эта группа имеет порядок <math>\textstyle n\cdot m</math> и является абелевой, с двумя порождающими элементами. Например: | ||
| − | + | <center>[[File:sym_tbl04.png]]</center> | |
Для наглядности, мы не стали вводить имена для двух новых элементов <math>\textstyle c=ab</math> и <math>\textstyle d=ab^2</math>, оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно ''главной диагонали'' (из левого верхнего угла в правый нижний). | Для наглядности, мы не стали вводить имена для двух новых элементов <math>\textstyle c=ab</math> и <math>\textstyle d=ab^2</math>, оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно ''главной диагонали'' (из левого верхнего угла в правый нижний). | ||
| Строка 66: | Строка 64: | ||
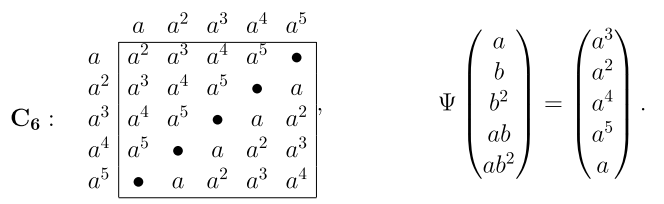
<math>\textstyle \bullet</math> Две группы называются ''изоморфными'', если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы <math>\textstyle \mathbf{C_{2,3}}</math> и циклической группы <math>\textstyle \mathbf{C_6}</math> (см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы <math>\textstyle \mathbf{C_{2,3}}</math> к группе <math>\textstyle \mathbf{C_{6}}</math>: <math>\textstyle a \mapsto a^3</math> и <math>\textstyle b\mapsto a^2</math> (их 2-я и 3-я степени дают единичный элемент). Аналогично <math>\textstyle ab\mapsto a^3\cdot a^2 = a^5</math>, и т.д. В результате между элементами групп <math>\textstyle \mathbf{C_{2,3}}</math> и <math>\textstyle \mathbf{C_6}</math> устанавливается взаимооднозначное соответствие, ''сохраняющее'' групповое умножение, что обозначается следующим образом: <math>\textstyle \mathbf{C_{2,3}}\approx \mathbf{C_{6}}</math>. Это соответствие записано ниже справа в виде функции: | <math>\textstyle \bullet</math> Две группы называются ''изоморфными'', если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы <math>\textstyle \mathbf{C_{2,3}}</math> и циклической группы <math>\textstyle \mathbf{C_6}</math> (см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы <math>\textstyle \mathbf{C_{2,3}}</math> к группе <math>\textstyle \mathbf{C_{6}}</math>: <math>\textstyle a \mapsto a^3</math> и <math>\textstyle b\mapsto a^2</math> (их 2-я и 3-я степени дают единичный элемент). Аналогично <math>\textstyle ab\mapsto a^3\cdot a^2 = a^5</math>, и т.д. В результате между элементами групп <math>\textstyle \mathbf{C_{2,3}}</math> и <math>\textstyle \mathbf{C_6}</math> устанавливается взаимооднозначное соответствие, ''сохраняющее'' групповое умножение, что обозначается следующим образом: <math>\textstyle \mathbf{C_{2,3}}\approx \mathbf{C_{6}}</math>. Это соответствие записано ниже справа в виде функции: | ||
| − | + | <center>[[File:sym_tbl05.png]]</center> | |
Две группы <math>\textstyle \mathbf{G}</math> и <math>\textstyle \mathbf{G}'</math> является ''гомоморфными'' если существует соответствие между их элементами, т.е. всюду определённая функция <math>\textstyle \Psi</math> из <math>\textstyle \mathbf{G}</math> в <math>\textstyle \mathbf{G}'</math>: <math>\textstyle g_k' = \Psi(g_i)</math> ''сохраняющая умножения'': <math>\textstyle \Psi(g_i\,g_j)=\Psi(g_i)\Psi(g_j). </math> Множество <math>\textstyle \mathbf{G}'</math> называется ''образом'' отображения: <math>\textstyle \mathbf{G}'=\Psi(\mathbf{G})</math>. Иногда пишут <math>\textstyle \mathbf{G}'={\rm Im}\,\Psi</math>. Если функция <math>\textstyle \Psi</math> имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде: | Две группы <math>\textstyle \mathbf{G}</math> и <math>\textstyle \mathbf{G}'</math> является ''гомоморфными'' если существует соответствие между их элементами, т.е. всюду определённая функция <math>\textstyle \Psi</math> из <math>\textstyle \mathbf{G}</math> в <math>\textstyle \mathbf{G}'</math>: <math>\textstyle g_k' = \Psi(g_i)</math> ''сохраняющая умножения'': <math>\textstyle \Psi(g_i\,g_j)=\Psi(g_i)\Psi(g_j). </math> Множество <math>\textstyle \mathbf{G}'</math> называется ''образом'' отображения: <math>\textstyle \mathbf{G}'=\Psi(\mathbf{G})</math>. Иногда пишут <math>\textstyle \mathbf{G}'={\rm Im}\,\Psi</math>. Если функция <math>\textstyle \Psi</math> имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде: | ||
| Строка 79: | Строка 77: | ||
{| width="100%" | {| width="100%" | ||
| width="30%"|[[Что такое симметрия?]] << | | width="30%"|[[Что такое симметрия?]] << | ||
| − | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/ | + | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/relworld_06.pdf Глава 6]) |
| width="30%" align="right"| >> [[Группа перестановок]] | | width="30%" align="right"| >> [[Группа перестановок]] | ||
|} | |} | ||
---- | ---- | ||
[[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | [[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | ||
Текущая версия на 18:57, 2 июля 2013
| Что такое симметрия? << | Оглавление (Последняя версия в: Глава 6) | >> Группа перестановок |
|---|
Самой простой является группа циклических перестановок элементов . Пронумеруем углы правильного -угольника. Пусть его вращают в плоскости на углы , где без переворотов. Ниже представлены такие преобразования треугольника () и квадрата ():

Понятно, что это абелева группа. Поворот раз на угол порождает любой элемент группы. Для именования элементов группы удобно использовать следующие обозначения:

Имеется одна группа 2-го () и одна 3-го порядка (). Для 4-х элементов возможны две группы и (см.выше). Для 5-ти — одна ().
Если правильному -угольнику разрешено вращаться в плоскости вокруг центра симметрии, и переворачиваться вокруг осей симметрии, то получается группа диэдра порядка . К относят и группу преобразований прямоугольника (\,H). Для треугольника () имеем (для квадрата см.стр.\,\pageref{sym_D3_pic}):

Кроме наименьшей неабелевой группы для 6 элементов существует ещё абелева группа . Группа 7-го порядка одна (); 8-й порядок допускает уже 5 групп, две из которых неабелевы. Это и группа кватернионов (см.стр.\,\pageref{quat_basis_def1}).
В левом верхнем углу таблиц находится блок, совпадающий с циклической группой. Говорят, что является {подгруппой} группы .
Подгруппа , это подмножество , элементов группы для которых выполняются все групповые свойства (есть единичный, у каждого элемента — обратный, и при умножении возникают только элементы из подгруппы : ). Так, .
Единичный элемент и сама группа являются подгруппами . Их называют собственными. Выявление остальных (несобственных) подгрупп данной группы позволяет лучше понять её свойства.
Если , а то (отношение транзитивности). Для обозначения "вложенности" подгрупп иногда переворачивают значок подгруппы: . Пересечение подгрупп также является подгруппой (иногда это только ). Стоит найти (\,H) подгруппы группы и построить (\,H) иерархию подгрупп группы .
Если у группы известна некоторая подгруппа , то можно попытаться найти другие подгруппы. Для этого, выбирается фиксированный элемент группы (), не принадлежащий () и строится сопряжённая подгруппа , элементы которой получаются умножением всех элементов слева на , а справа на . То, что такое множество элементов образует группу, легко проверяется (\,H). Так, результат умножения остаётся внутри :
Например, для имеем .
Подгруппа называется инвариантной, если её сопряжение с любым элементом снова дает (новая подгруппа не возникает). В этом случае для любого имеем: или иначе . Заметим, что при сопряжении элемента получается вообще говоря другой элемент инвариантной подгруппы. Несложно видеть, что все подгруппы абелевой группы являются инвариантными.
Группа, не имеющая инвариантных подгрупп (кроме себя самой и единичного элемента) называется простой. Группа не простая, так как инвариантна (\,H). Полупростой называется группа у которой все инвариантные подгруппы неабелевы.
Если инвариантная подгруппа группы , а инвариантная подгруппа группы , то в общем случае не является инвариантной подгруппой группы (хотя конечно является подгруппой ). Т.е. инвариантность подгрупп не обладает транзитивностью.
Циклическая группа </math>C_nНевозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , в отличие от групп диэдра } D_nn>3Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle , является абелевой группой. Естественно это не единственный пример семейства абелевых групп. В циклической группе один производящий элемент генерит все остальные элементы группы. Однако производящих элементов может быть несколько. Рассмотрим, например, группу } C_{n,m}$, задав её при помощи определяющих соотношений:
Эта группа имеет порядок и является абелевой, с двумя порождающими элементами. Например:

Для наглядности, мы не стали вводить имена для двух новых элементов и , оставив в таблице только производящие элементы. Хорошо видно, что эта группа симметрична относительно главной диагонали (из левого верхнего угла в правый нижний).
Аналогично можно определить абелеву группу с тремя, и т.д. порождающими элементами. Они имеют наглядное представление в виде дисков открывающих замок в сейфе или камере хранения. Так, элементы группы могут быть представлены при помощи следующих картинок (два диска замка нарисованы один в другом):

Вращение дисков независимы друг от друга, и это собственно и приводит к абелевости группы. Если мы имеем дисков, с количеством цифр ,...,, то порядок такой группы будет равен . Любой элемент группы раскладывается на коммутирующие множители порождающих элементов: , где .
Эти группы покрывают все возможные абелевы группы. Простые циклические группы являются их вырожденным случаем, когда порождающий элемент единственен или — взаимопростые.
Две группы называются изоморфными, если с точностью до переобозначения элементов их таблицы умножения совпадают. Сравним таблицы группы и циклической группы (см. ниже). Так как порядки порождающих элементов взаимопростые, можно сделать такие соответствия от группы к группе : и (их 2-я и 3-я степени дают единичный элемент). Аналогично , и т.д. В результате между элементами групп и устанавливается взаимооднозначное соответствие, сохраняющее групповое умножение, что обозначается следующим образом: . Это соответствие записано ниже справа в виде функции:
Две группы и является гомоморфными если существует соответствие между их элементами, т.е. всюду определённая функция из в : сохраняющая умножения: Множество называется образом отображения: . Иногда пишут . Если функция имеет обратную, т.е. соответствие взаимно-однозначно, то это изоморфизм. Поэтому изоморфизм является частным случаем гомоморфизма, когда отображение групп существует в обе стороны. Наглядно это можно представить в следующем виде:
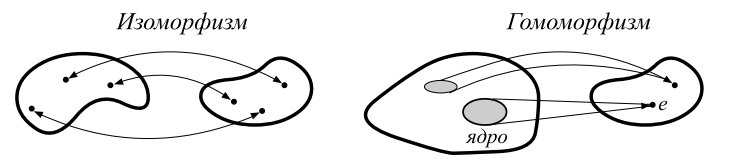
В качестве примера рассмотрим множество несингулярных (с ненулевыми определителями) матриц x. Они имеют обратные, а, следовательно, их умножение удовлетворяет групповым аксиомам. Определитель произведения устанавливает гомоморфное отображение из группы матриц в группу ненулевых вещественных чисел.
Множество элементов переходящих при гомоморфизме в единичный элемент называется ядром гомоморфизма и обозначается . В примере с матрицами ядром является множество всех матриц с единичным определителем. Они образуют группу .
| Что такое симметрия? << | Оглавление (Последняя версия в: Глава 6) | >> Группа перестановок |
|---|
Релятивистский мир - лекции по теории относительности, гравитации и космологии
















































































