Хищники и их жертвы

Электронный шум <<	Оглавление	>> Финансовые рынки

---

Рассмотрим пример очень простой модели, описывающей динамику популяции двух видов живых существ. Одни из них будут безобидными кроликами ("жертвы"), а вторые — коварными лисами ("хищники"). Детерминированная система уравнений имеет вид:

$\left\{{\begin{array}{l}{\dot {x}}=\;\;\alpha \cdot x-\mu \cdot xy-\beta \cdot x^{2}\\{\dot {y}}=-\gamma \cdot y+\nu \cdot xy.\end{array}}\right.$

Количество кроликов обозначено через $\textstyle x$, а лис — через $\textstyle y$. Точка над переменной, как обычно, - производная по времени. Кролики размножаются в соответствии с логистическим уравнением, однако их смертность зависит также от встречи с хищником, которая тем вероятнее, чем больше жертв и хищников. Поэтому в уравнение добавлен член $\textstyle -\mu \cdot x\,y$. Популяция лис при отсутствии питания вымирает ($\textstyle -\gamma y$). Положительный прирост возможен только при активной и недружественной встрече с кроликами ($\textstyle +\nu \cdot xy$). Если ресурсы питания для кроликов не ограничены ($\textstyle \beta =0$), то эту систему называют уравнениями Лотка-Вольтерра (Lotka-Volterra equation, predator-prey equations).

Модель содержит большое число параметров. Не все из них имеют существенное значение при анализе качественных свойств поведения решения. Поэтому целесообразно уменьшить их количество. Для этого сделаем преобразования масштаба: $\textstyle x\Rightarrow ax$, $\textstyle y\Rightarrow by$ и $\textstyle t\Rightarrow \tau t$, где константы $\textstyle a$, $\textstyle b$ и $\textstyle \tau$ являются "единицами измерения" численности особей и времени. Подставим эти преобразования в уравнения (при этом $\textstyle {\dot {x}}\Rightarrow (a/\tau ){\dot {x}}$) и выберем $\textstyle a=1/\nu \tau$, $\textstyle b=1/\mu \tau$ и $\textstyle \tau =1/\gamma$.

Тогда, с точностью до масштабирования, система уравнений становится двухпараметрической и записывается в следующем виде:

$\left\{{\begin{array}{l}{\dot {x}}=-xy+\omega ^{2}\,x-2\lambda \,x^{2}\\{\dot {y}}=\;\;xy-y,\end{array}}\right.$

где $\textstyle \omega ^{2}=\alpha /\gamma$, $\textstyle 2\lambda =\beta /\nu$. Её качественный анализ начинается с определения особых точек, в которых $\textstyle {\dot {x}}={\dot {y}}=0$:

$\left\{{\begin{array}{l}x_{\infty }\cdot (-y_{\infty }+\omega ^{2}-2\lambda x_{\infty })=0\\y_{\infty }\cdot (x_{\infty }-1)=0.\end{array}}\right.$

Несложно видеть, что существует три решения этих уравнений:

${\bigl \{}x_{\infty }=1,\;\;\;y_{\infty }=\omega ^{2}-2\lambda {\bigr \}};\;\;\;\;{\bigl \{}x'_{\infty }=y'_{\infty }=0{\bigr \}};\;\;\;\;{\bigl \{}x''_{\infty }=\omega ^{2}/2\lambda ,\;\;\;y''_{\infty }=0{\bigr \}}.$

Последние два достаточно тривиальны и сводятся в первом случае к полному вымиранию всех особей, а во втором — к вымиранию хищников.

Рассмотрим решения системы в окрестности первой особой точки. Введём отклонения численности популяций $\textstyle X=x-x_{\infty }$, $\textstyle Y=y-y_{\infty }$ и разложим правую часть уравнений в ряд по $\textstyle \mathbf {X} =\{X,Y\}$:

$\left\{{\begin{array}{l}{\dot {X}}=-2\lambda X-Y\\{\dot {Y}}=(\omega ^{2}-2\lambda )X\end{array}}\right.\;\;\;\;\;\;or\;\;\;{\dot {\mathbf {X} }}=\mathbf {A} \cdot \mathbf {X} ,\;\;where\;\;\;\mathbf {A} ={\begin{pmatrix}-2\lambda &-1\\\omega ^{2}-2\lambda &0\\\end{pmatrix}}.$

Это линеаризованное уравнение будем решать стандартными методами, рассмотренными в разделе Линейные многомерные модели. Характеристическое уравнение $\textstyle a^{2}+2\lambda \,a+\omega ^{2}-2\lambda =0$ для собственных значений матрицы $\textstyle \mathbf {A}$ имеет два решения:

$a_{1,2}=-\lambda \pm i{\sqrt {\omega ^{2}-2\lambda -\lambda ^{2}}}.$

Если пищевые ресурсы жертв не ограничены $\textstyle \lambda =0$, то в системе устанавливаются незатухающие периодические колебания с частотой $\textstyle \omega$. При $\textstyle \lambda \neq 0$ эти колебания будут затухающими. Колебательного режима не будет, если $\textstyle \lambda$ очень велико. В этом случае оба решения отрицательны и действительны.

Бифуркация в системе возникает, когда подкоренное выражение становится равным нулю, что соответствует значению $\textstyle \lambda _{0}={\sqrt {1+\omega ^{2}}}-1$. При $\textstyle \lambda >\lambda _{0}$ решение уравнений монотонно затухает, а при $\textstyle \lambda <\lambda _{0}$ происходит качественная перестройка и возникают колебания, сначала сильно затухающие, а по мере уменьшения $\textstyle \lambda$ постепенно переходящие в периодические.

Выше представлена динамика численности особей при $\textstyle \lambda =0$, и $\textstyle \omega =0.5$. На левом рисунке начальные значения $\textstyle x_{0}=1$ и $\textstyle y_{0}=0.1$, а на правом: $\textstyle x_{0}=1$ и $\textstyle y_{0}=1$. Если начальное отклонение от точки равновесия $\textstyle x_{\infty }=1$, $\textstyle y_{\infty }=0.25$ невелико, колебания будут практически гармоническими. Однако при существенных отклонениях начинают сказываться нелинейности, и "синусоида" становится сильно искажённой.

Стоит обратить внимание на сдвиг кривых относительно друг друга. Когда лис мало — кролики быстро размножаются. Это приводит к росту численности лис, что тормозит рост популяции кроликов. Как и любая колебательная система, модель "хищник-жертва" обладает инертностью. Поэтому популяция лис продолжает увеличиваться, тогда как ряды кроликов стремительно редеют.

При описании реальных популяций эта модель обладает одним неприятным свойством. Если начальное значение хищников заметно отличается от равновесия, то их численность испытывает очень большие колебания, прижимаясь в минимуме к нулевому значению. Так, выше, на правом графике ($\textstyle x_{0}=1$, $\textstyle y_{0}=1$), численность лис падает до 0.02 (в 50 раз), тогда как популяция кроликов изменяется только в 4 раза. Этот эффект называют атто-лисьей проблемой (atto-fox problem), так как иногда при моделировании численность хищников падает практически до нуля ("атто" — это $\textstyle 10^{-18}$ часть чего либо).

Рассмотрим ситуацию ограниченных ресурсов. Если $\textstyle \omega =0.5$, то критическое значение $\textstyle \lambda _{0}=0.12$. Выберем $\textstyle \lambda =0.01$ (слева) и $\textstyle \lambda =0.05$ (справа):

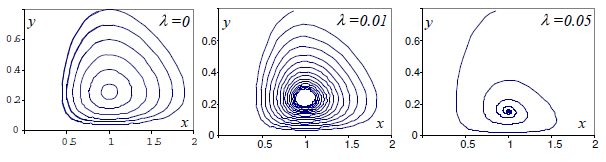
Затухание наглядно видно также на фазовой диаграмме в плоскости $\textstyle (x,y)$. Ниже на первом рисунке представлены фазовые кривые при различных начальных условиях и неограниченных ресурсах ($\textstyle \lambda =0$). При этом всегда $\textstyle x_{0}=1$, а $\textstyle y_{0}$ меняется от 0.2 до 0.8 c шагом 0.1. На втором и третьем рисунках приведена единичная траектория, соответствующая затухающим колебаниям с $\textstyle \lambda =0.01$ и $\textstyle \lambda =0.05$ от точки $\textstyle x_{0}=1$, $\textstyle y_{0}=0.8$:

$\textstyle \bullet$ Перейдём теперь к стохастической задаче. Будем считать, что рождаемость подвержена случайным факторам, так что относительный прирост $\textstyle dx/x$ является винеровским шумом с амплитудой $\textstyle s_{x}$ для кроликов и $\textstyle s_{y}$ для лис:

$\left\{{\begin{array}{l}dx=(-xy+\omega ^{2}\,x-2\lambda \,x^{2})\,dt+x\,s_{x}\,\delta W_{x}\\dy=(\;\;xy-y)\,dt+y\,s_{y}\,\delta W_{y}.\end{array}}\right.$

Линеаризованные в окрестности особой точки уравнения имеют решение для средних, аналогичное детерминированному случаю.

Для колебательного режима средняя численность популяции кроликов стремится к единице, а лис — к $\textstyle \omega ^{2}-2\lambda$. Так как снос уравнений не линеен, это, на самом деле, лишь первое приближение к точному асимптотическому пределу. Найдём его при помощи уравнения для средних (6.15), (см. Системы стохастических уравнений). Выбирая $\textstyle F=\ln x$ и $\textstyle F=\ln y$ и положив производные по времени равными нулю, получаем:

${\bar {x}}=1+{\frac {s_{y}^{2}}{2}},\;\;\;\;\;\;\;\;\;\;\;{\bar {y}}=\omega ^{2}-2\lambda -\lambda s_{y}^{2}-{\frac {s_{x}^{2}}{2}}.$

Равновесное значение средней численности кроликов увеличивается за счёт флуктуации рождаемости лис, а численность лис уменьшается (по сравнению с детерминированным случаем) от шумов обоих популяций.

Аналогично, выбор $\textstyle F=x$ и $\textstyle F=y$ позволяет найти $\textstyle \sigma _{x}^{2}=\left\langle (x-{\bar {x}})^{2}\right\rangle$ — дисперсию колебания численности популяции кроликов вокруг средних:

$\sigma _{x}^{2}={\frac {1}{4\lambda }}{\bigl [}s_{x}^{2}+(\omega ^{2}-2\lambda )\,s_{y}^{2}-\lambda s_{y}^{4}{\bigr ]}.$

и коэффициент ковариации:

$\mathrm {cov} \,x,y)=-{\frac {s_{x}^{2}}{2}}\,{\bar {y}}.$

Он имеет отрицательное значение, что свидетельствует о "противофазности" динамики лис и кроликов.

Рассмотрим численности популяций $\textstyle x(t)$, $\textstyle y(t)$ со следующими параметрами: $\textstyle \omega =0.5$, $\textstyle \lambda =0.01$, $\textstyle s_{x}=0.05$, $\textstyle s_{y}=0$:

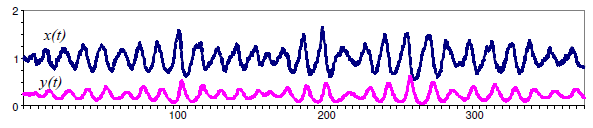
Как и в случае линейного стохастического осциллятора, колебательный режим продолжается и при наличии затухания (параметр $\textstyle \lambda$). Однако это колебание оказывается квазипериодическим с плавающим периодом и амплитудой.

В природе не происходит гладких колебаний численности популяций. Их динамика существенно стохастична. При этом стохастичность не является "досадным" шумом, который искажает теоретически гладкую динамику, а приводит к эффекту появления колебаний, когда в детерминированной системе они исчезают. Ограниченность пищевых ресурсов кроликов играет стабилизирующую роль в системе, ослабляя атто-лисий эффект.

---

Электронный шум <<	Оглавление	>> Финансовые рынки

---

Стохастический мир - простое введение в стохастические дифференциальные уравнения