Группа перестановок — различия между версиями
WikiSysop (обсуждение | вклад) |
WikiSysop (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
{| width="100%" | {| width="100%" | ||
| width="30%"|[[Примеры и определения]] << | | width="30%"|[[Примеры и определения]] << | ||
| − | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/ | + | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/relworld_06.pdf Глава 6]) |
| width="30%" align="right"| >> [[Еще немного определений]] | | width="30%" align="right"| >> [[Еще немного определений]] | ||
|} | |} | ||
---- | ---- | ||
| + | |||
| + | <math>\bullet</math> Рассмотрим ещё один важный класс групп. | ||
| + | Пусть имеется <math>n</math> упорядоченных объектов, пронумерованных цифрами от 1 до <math>n</math>\textstyle . Эти объекты можно переставить местами <math>n!=2\cdot 3\cdot...\cdot n/</math>способами (на первое место поставим один их <math>n</math> предметов; для ''каждой'' из этих <math>n</math> возможностей, на второе место поставим один из <math>(n-1)</math> оставшихся предметов, и т.д.). Например, для трёх объектов возможно 6 перестановок: | ||
| + | |||
| + | <center>[[File:sym_tbl06.png]]</center> | ||
| + | |||
| + | Каждой перестановке мы присвоили имя "<math>\textstyle a</math>-<math>\textstyle f</math>", и будем её считать операцией, переводящей первоначальный порядок <math>\textstyle e=(1\;2\;3)</math> в некоторый другой. Перестановки <math>\textstyle \{a,\;b,\;c\}</math> задействуют только пары элементов, оставляя третий неизменным. Оставшиеся две являются циклическим сдвигом вправо <math>\textstyle \{d\}</math> и влево <math>\textstyle \{f\}</math>. | ||
| + | |||
| + | Композиция двух последовательных перестановок, снова является перестановкой. Представим все возможные композиции перестановок трёх объектов при помощи таблицы умножения. Ясно, что если мы переставим первый и второй объект, а затем повторим эту операцию, то получится исходный порядок. Поэтому <math>\textstyle a^2=b^2=c^2=e</math>. Сдвинув исходный порядок вправо (<math>\textstyle d</math>), а затем повторив этот сдвиг мы получим <math>\textstyle f=d^2</math>. Аналогично рассуждая дальше, сформируем таблицу умножения: | ||
| + | |||
| + | <center>[[File:sym_tbl07.png]]</center> | ||
| + | |||
| + | Эта группа называется ''группой перестановок'' или ''симметрической группой'' и обозначается как <math>\textstyle \mathbf{S_3}</math>. Очевидно, что она не абелева. Например: <math>\textstyle (a\, b=f)\neq (b\, a=d)</math>. Аналогично строится группа перестановок <math>\textstyle n</math> объектов <math>\textstyle \mathbf{S_n}</math>. Она имеет порядок <math>\textstyle n!</math> и при <math>\textstyle n>2</math> также является не абелевой. | ||
| + | |||
| + | Обратим внимание на блок 2x2 в правом нижнем углу состоящий из элементов <math>\textstyle f</math> и <math>\textstyle d</math>. Это подгруппа <math>\textstyle \mathbf{C_3}\subset \mathbf{S_3}</math>. Понятно, что циклические сдвиги вправо или влево вместе с единичным порядком являются замкнутыми операциями и образуют группу <math>\textstyle \mathbf{C_3}=\{e, d,f\}</math>. Она является инвариантной (проверьте). | ||
| + | |||
| + | Группа <math>\textstyle \mathbf{S}_3</math> изоморфна <math>\textstyle \mathbf{D}_3</math>. Действительно, номера вершин треугольника на рисунке <math>\textstyle \mathbf{D}_3</math> (стр.\,\pageref{group_D3_pic}), перечисляемые по часовой стрелки, начиная с верхней, являются перестановками трёх чисел (так, только при <math>\textstyle n=3</math>). | ||
| + | |||
| + | <math>\textstyle \bullet</math> Перестановки можно считать всюду определёнными обратимыми целочисленными функциями <math>\textstyle x(i)</math>, где <math>\textstyle i</math> — позиция элемента, а <math>\textstyle x(i)</math> — его номер. Результат композиции двух последовательных перестановок <math>\textstyle z=x\cdot y</math> равен: | ||
| + | |||
| + | :<center><math>z(i) = x\bigl(y(i)\bigr).</math></center> | ||
| + | |||
| + | Обратная <math>\textstyle \bar{x}</math> к <math>\textstyle x</math> перестановка удовлетворяет уравнению: | ||
| + | |||
| + | :<center><math>\bar{x}\bigl(x(i)\bigr) ={x}\bigl(\bar{x}(i)\bigr) = i.</math></center> | ||
| + | |||
| + | Соответственно, единичная перестановка — это "'линейная функция" <math>\textstyle e(i)=i</math>. | ||
| + | |||
| + | <math>\textstyle \bullet</math> При вычислении результата композиции двух перестановок можно поступать следующим образом. Рассмотрим, например <math>\textstyle a\cdot f=b</math>. Запишем первую перестановку, поставив у номера объекта индекс равный его текущему положению в списке: | ||
| + | |||
| + | :<center><math>\overbrace{(2_1\;1_2\;3_3)}^{a}\cdot\overbrace{(2\;3\;1)}^{f}=\overbrace{(1\;3\;2)}^{b},</math></center> | ||
| + | |||
| + | На первом месте в <math>\textstyle f</math> стоит 2. Это означает, что <math>\textstyle f</math> применённая к уже сделанной <math>\textstyle a</math>, должна на первое место поставить второй элемент <math>\textstyle a</math>, т.е. "1". Аналогично третий элемент ("3") идёт на второе место, и первый ("2") на третье. Таким образом для записи композиции <math>\textstyle x\cdot y</math> необходимо взять второй список, и вместо его цифр <math>\textstyle y=(i,j, k,...)</math> записать элементы первого списка с индексами <math>\textstyle i,j,k,...</math>: | ||
| + | |||
| + | :<center><math>(...\,x_i\,...y_j...z_k...)\cdot(i\,\,j\,k\,...) = (x\, y\, z\,....).</math></center> | ||
| + | |||
| + | Например, выполним более длинное умножения двух перестановок девяти объектов: | ||
| + | |||
| + | :<center><math>( 8_1\;2_2\;1_3\;4_4\;5_5\;6_6\;7_7\;3_8\;9_9)\cdot(1\;7\;3\;4\;5\;2\;9\;8\;6)=(8\;7\;1\;4\;5\;2\;9\;3\;6).</math></center> | ||
| + | |||
| + | <math>\textstyle \bullet</math> Чтобы для данной перестановки записать обратную к ней, необходимо ''значение номера позиции'' элемента поставить на место номера этого элемента: | ||
| + | |||
| + | :<center><math>(...\,x_i\,...y_j...z_k...)^{-1} = (...\,i_x\,...j_y...k_z...).</math></center> | ||
| + | |||
| + | Для этого достаточно переставить местами число и его индекс, и после этого отсортировать по возрастанию индекса. Например | ||
| + | |||
| + | :<center><math>d^{-1}=(3_1\;1_2\;2_3)^{-1}=(1_3\;2_1\;3_2)=(2\;3\;1)=f.</math></center> | ||
| + | |||
| + | В результате: <math>\textstyle d\cdot d^{-1} = (3_1\;1_2\;2_3)\;(2\;3\;1)=(1\;2\;3)=e</math>. | ||
| + | |||
| + | <math>\textstyle \bullet</math> Любую перестановку можно характеризовать по числу одновременно задействованных в ней объектов. Так, в <math>\textstyle \mathbf{S_3}</math> элемент "<math>\textstyle a=(2\;1\;3)</math>" переставляет местами первые два объекта, а положение третьего оставляет неизменным. Замкнутые группы переставляемых объектов называются ''циклами''. В перестановке может быть несколько циклов: | ||
| + | |||
| + | :<center><math>p=(8_1\;7_2\;1_3\;4_4\;5_5\;2_6\;9_7\;3_8\;6_9)=[8\;3\;1]\cdot[7\;9\;6\;2]</math></center> | ||
| + | |||
| + | Чтобы их найти, берём первый элемент, номер которого не совпадает с номером позиции (8) и идём на 8-е место. Там стоит 3. Поэтому идём на 3-е место. Там 1, и так как на первом месте стоит 8-ка с которой мы начали, цикл <math>\textstyle [8\;3\;1]</math> замыкается. | ||
| + | |||
| + | Цикл записывают опуская индексы, так как их всегда можно восстановить. Для этого необходимо в качестве индекса ставить номер ''предыдущего'' объекта в списке цикла, считая предыдущим для первого элемента — последний: | ||
| + | |||
| + | :<center><math>[8\;3\;1]=(8_1\;3_8\;1_3)</math></center> | ||
| + | |||
| + | <center>[[File:cicles.png]]</center> | ||
| + | |||
| + | :<center><math>\;\;\;\;[7\;9\;6\;2]=(7_2\;9_7\;6_9\;2_6)</math></center> | ||
| + | |||
| + | <center>[[File:cicles2.png]]</center> | ||
| + | |||
| + | При таком алгоритме записи циклов любые циклические перестановки <math>\textstyle [8\;3\;1]</math>, <math>\textstyle [1\;8\;3]</math>, <math>\textstyle [3\;1\;8]</math> являются одной и той же перестановкой. Смысл цикла состоит в круговой перестановке объектов — 8 идёт на третье место, 3 идёт на первое, а 1 на восьмое. Заметим, что мы различаем обозначения для цикла (квадратные скобки) и для перестановки (круглые). | ||
| + | |||
| + | Если два цикла, например <math>\textstyle [8\;3\;1]</math> и <math>\textstyle [7\;9\;6\;2]</math> не имеют пересекающихся элементов, то произведение содержащих им перестановок можно выполнять в любом порядке: | ||
| + | |||
| + | :<center><math>\begin{array}{l} (\mathbf{8}_1\;2_2\;\mathbf{1}_3\;4_4\;5_5\;6_6\;7_7\;\mathbf{3}_8\;9_9)\cdot(1\;\mathbf{7}\;3\;4\;5\;\mathbf{2}\;\mathbf{9}\;8\;\mathbf{6})=(8\;7\;1\;4\;5\;2\;9\;3\;6),\\ (1_1\;\mathbf{7}_2\;3_3\;4_4\;5_5\;\mathbf{2}_6\;\mathbf{9}_7\;8_8\;\mathbf{6}_9)\cdot (\mathbf{8}\;2\;\mathbf{1}\;4\;5\;6\;7\;\mathbf{3}\;9)=(8\;7\;1\;4\;5\;2\;9\;3\;6).\\ \end{array}</math></center> | ||
| + | |||
| + | Таким образом, выявление циклов позволяет разбить перестановку на композицию более простых перестановок. | ||
| + | |||
| + | Циклы состоящие из двух объектов называются ''транспозициями''. Двойное применение транспозиции даёт единичную перестановку. Аналогично, тройное применение цикла длинной 3 даёт исходный порядок: | ||
| + | |||
| + | :<center><math>\begin{array}{l} \;[8\;3\;1]^2 \;=\; (8_1\;3_8\;1_3)\,(8_1\;3_8\;1_3) = (3_1\;1_8\;8_3)\\ \;[8\;3\;1]^3 \;=\; (3_1\;1_8\;8_3)\,(8_1\;3_8\;1_3) = (1_1\;8_8\;3_3) = e \end{array}</math></center> | ||
| + | |||
| + | Понятно, что если цикл имеет длину <math>\textstyle n</math>, то его <math>\textstyle n</math>-я степень даст единичную перестановку (мы <math>\textstyle n</math> раз по кругу переставим объекты, вернувшись к исходному порядку). | ||
| + | |||
| + | <math>\textstyle \bullet</math> Изоморфизм групп иногда приобретает очень любопытные формы. Пронумеруем элементы <math>\textstyle \{e,a,b,c\}</math> группы <math>\textstyle \mathbf{D_2}</math> цифрами от 1 до 4. Представим каждую строку таблицы умножения в виде списка номеров элементов, поставив первым номер элемента в заголовке строки: | ||
| + | |||
| + | <center>[[File:sym_tbl08.png]]</center> | ||
| + | |||
| + | В каждой строке, включая её заголовок, элемент встречается один и только один раз. Поэтому строки таблицы умножения (вместе с единичной <math>\textstyle p_e</math>) являются перестановками четырех элементов. Так как в этом случае возможно <math>\textstyle 24</math> перестановки, то <math>\textstyle p_e,p_a,p_b,p_c</math> — лишь некоторое подмножество из группы <math>\textstyle \mathbf{S_4}</math>. Однако это подмножество перестановок замечательным образом оказывается группой с той же таблицей, что и у <math>\textstyle \mathbf{D_2}</math>! Например, | ||
| + | |||
| + | :<center><math>\begin{array}{l} p_a\, p_b = (2_1\;1_2\;4_3\;3_4)\, (3\;4\;1\;2) = (4\;3\;2\;1) = p_c,\\ p_a\, p_a = (2_1\;1_2\;4_3\;3_4)\, (2\;1\;4\;3) = (1\;2\;3\;4) = p_e. \end{array}</math></center> | ||
| + | |||
| + | Этот эффект возникает благодаря ''теореме Кэли'': <blockquote> \it Любая конечная группа '''G''' изоморфна некоторой подгруппе группы перестановок <math>\textstyle \mathbf{S_n}</math>. </blockquote> Действительно, рассмотрим группу с <math>\textstyle n</math> элементами <math>\textstyle \mathbf{G}=\{g_1,...,g_{n}\}</math>. Каждому элементу <math>\textstyle g_i</math> поставим в соответствие перестановку исходного порядка (строка с заголовком <math>\textstyle g_i</math>): | ||
| + | |||
| + | :<center><math>p_i = (g_i\,g_1,\;g_i\,g_2,\;..., g_i\, g_{n}).</math></center> | ||
| + | |||
| + | Единичной (исходной) перестановкой будем считать упорядоченные по индексу элементы <math>\textstyle p_e=(g_1,\;g_2,\;,...,\;g_n)</math>. Рассмотрим композицию двух перестановок <math>\textstyle p_i</math> и <math>\textstyle p_j</math>, созданных при помощи <math>\textstyle g_i</math> и <math>\textstyle g_j</math>: | ||
| + | |||
| + | :<center><math>p_i\, p_j = (g_i\,g_1,\;..., g_i\, g_{n})\, (g_j\,g_1,\;..., g_j\, g_{n})=(g_i\,g_j\,g_1,\;..., g_i\, g_j\, g_{n}) = p_k.</math></center> | ||
| + | |||
| + | Действительно, пусть <math>\textstyle g_j\,g_1=g_s</math>. При умножении перестановок, мы должны на первое место результата поставить элемент из списка <math>\textstyle p_i</math> под номером <math>\textstyle s</math>. В силу упорядоченности в <math>\textstyle p_i</math> по второму индексу — это <math>\textstyle g_i\,g_s</math> или <math>\textstyle g_i\,g_j\,g_1</math>. Аналогично для остальных элементов списка. Следовательно, перестановка <math>\textstyle p_k=p_i\, p_j</math> получается при помощи <math>\textstyle g_k=g_i\,g_j</math> и таблица умножения перестановок <math>\textstyle p_i</math> изоморфна группе <math>\textstyle \mathbf{G}</math>. <math>\textstyle \square</math> | ||
| Строка 10: | Строка 107: | ||
{| width="100%" | {| width="100%" | ||
| width="30%"|[[Примеры и определения]] << | | width="30%"|[[Примеры и определения]] << | ||
| − | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/ | + | ! width="40%"|[[Релятивистский мир|Оглавление]] (Последняя версия в: [http://synset.com/pdf/relworld_06.pdf Глава 6]) |
| width="30%" align="right"| >> [[Еще немного определений]] | | width="30%" align="right"| >> [[Еще немного определений]] | ||
|} | |} | ||
---- | ---- | ||
[[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | [[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | ||
Текущая версия на 18:57, 2 июля 2013
| Примеры и определения << | Оглавление (Последняя версия в: Глава 6) | >> Еще немного определений |
|---|
Рассмотрим ещё один важный класс групп. Пусть имеется упорядоченных объектов, пронумерованных цифрами от 1 до \textstyle . Эти объекты можно переставить местами способами (на первое место поставим один их предметов; для каждой из этих возможностей, на второе место поставим один из оставшихся предметов, и т.д.). Например, для трёх объектов возможно 6 перестановок:
Каждой перестановке мы присвоили имя "-", и будем её считать операцией, переводящей первоначальный порядок в некоторый другой. Перестановки задействуют только пары элементов, оставляя третий неизменным. Оставшиеся две являются циклическим сдвигом вправо и влево .
Композиция двух последовательных перестановок, снова является перестановкой. Представим все возможные композиции перестановок трёх объектов при помощи таблицы умножения. Ясно, что если мы переставим первый и второй объект, а затем повторим эту операцию, то получится исходный порядок. Поэтому . Сдвинув исходный порядок вправо (), а затем повторив этот сдвиг мы получим . Аналогично рассуждая дальше, сформируем таблицу умножения:

Эта группа называется группой перестановок или симметрической группой и обозначается как . Очевидно, что она не абелева. Например: . Аналогично строится группа перестановок объектов . Она имеет порядок и при также является не абелевой.
Обратим внимание на блок 2x2 в правом нижнем углу состоящий из элементов и . Это подгруппа . Понятно, что циклические сдвиги вправо или влево вместе с единичным порядком являются замкнутыми операциями и образуют группу . Она является инвариантной (проверьте).
Группа изоморфна . Действительно, номера вершин треугольника на рисунке (стр.\,\pageref{group_D3_pic}), перечисляемые по часовой стрелки, начиная с верхней, являются перестановками трёх чисел (так, только при ).
Перестановки можно считать всюду определёнными обратимыми целочисленными функциями , где — позиция элемента, а — его номер. Результат композиции двух последовательных перестановок равен:
Обратная к перестановка удовлетворяет уравнению:
Соответственно, единичная перестановка — это "'линейная функция" .
При вычислении результата композиции двух перестановок можно поступать следующим образом. Рассмотрим, например . Запишем первую перестановку, поставив у номера объекта индекс равный его текущему положению в списке:
На первом месте в стоит 2. Это означает, что применённая к уже сделанной , должна на первое место поставить второй элемент , т.е. "1". Аналогично третий элемент ("3") идёт на второе место, и первый ("2") на третье. Таким образом для записи композиции необходимо взять второй список, и вместо его цифр записать элементы первого списка с индексами :
Например, выполним более длинное умножения двух перестановок девяти объектов:
Чтобы для данной перестановки записать обратную к ней, необходимо значение номера позиции элемента поставить на место номера этого элемента:
Для этого достаточно переставить местами число и его индекс, и после этого отсортировать по возрастанию индекса. Например
В результате: .
Любую перестановку можно характеризовать по числу одновременно задействованных в ней объектов. Так, в элемент "" переставляет местами первые два объекта, а положение третьего оставляет неизменным. Замкнутые группы переставляемых объектов называются циклами. В перестановке может быть несколько циклов:
Чтобы их найти, берём первый элемент, номер которого не совпадает с номером позиции (8) и идём на 8-е место. Там стоит 3. Поэтому идём на 3-е место. Там 1, и так как на первом месте стоит 8-ка с которой мы начали, цикл замыкается.
Цикл записывают опуская индексы, так как их всегда можно восстановить. Для этого необходимо в качестве индекса ставить номер предыдущего объекта в списке цикла, считая предыдущим для первого элемента — последний:

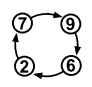
При таком алгоритме записи циклов любые циклические перестановки , , являются одной и той же перестановкой. Смысл цикла состоит в круговой перестановке объектов — 8 идёт на третье место, 3 идёт на первое, а 1 на восьмое. Заметим, что мы различаем обозначения для цикла (квадратные скобки) и для перестановки (круглые).
Если два цикла, например и не имеют пересекающихся элементов, то произведение содержащих им перестановок можно выполнять в любом порядке:
Таким образом, выявление циклов позволяет разбить перестановку на композицию более простых перестановок.
Циклы состоящие из двух объектов называются транспозициями. Двойное применение транспозиции даёт единичную перестановку. Аналогично, тройное применение цикла длинной 3 даёт исходный порядок:
Понятно, что если цикл имеет длину , то его -я степень даст единичную перестановку (мы раз по кругу переставим объекты, вернувшись к исходному порядку).
Изоморфизм групп иногда приобретает очень любопытные формы. Пронумеруем элементы группы цифрами от 1 до 4. Представим каждую строку таблицы умножения в виде списка номеров элементов, поставив первым номер элемента в заголовке строки:

В каждой строке, включая её заголовок, элемент встречается один и только один раз. Поэтому строки таблицы умножения (вместе с единичной ) являются перестановками четырех элементов. Так как в этом случае возможно перестановки, то — лишь некоторое подмножество из группы . Однако это подмножество перестановок замечательным образом оказывается группой с той же таблицей, что и у ! Например,
Этот эффект возникает благодаря теореме Кэли:
\it Любая конечная группа G изоморфна некоторой подгруппе группы перестановок .
Действительно, рассмотрим группу с элементами . Каждому элементу поставим в соответствие перестановку исходного порядка (строка с заголовком ):
Единичной (исходной) перестановкой будем считать упорядоченные по индексу элементы . Рассмотрим композицию двух перестановок и , созданных при помощи и :
Действительно, пусть . При умножении перестановок, мы должны на первое место результата поставить элемент из списка под номером . В силу упорядоченности в по второму индексу — это или . Аналогично для остальных элементов списка. Следовательно, перестановка получается при помощи и таблица умножения перестановок изоморфна группе .
| Примеры и определения << | Оглавление (Последняя версия в: Глава 6) | >> Еще немного определений |
|---|
Релятивистский мир - лекции по теории относительности, гравитации и космологии












































![{\displaystyle p=(8_{1}\;7_{2}\;1_{3}\;4_{4}\;5_{5}\;2_{6}\;9_{7}\;3_{8}\;6_{9})=[8\;3\;1]\cdot [7\;9\;6\;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f295d9e7dd8d5ec5d4f96bdf3f2b622baaf64a86)
![{\displaystyle \textstyle [8\;3\;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab8ab94afeb736ae019270bfb22df91a063ee7e)
![{\displaystyle [8\;3\;1]=(8_{1}\;3_{8}\;1_{3})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34790c66d6143a4bc6f68894a3c11a49754991e7)
![{\displaystyle \;\;\;\;[7\;9\;6\;2]=(7_{2}\;9_{7}\;6_{9}\;2_{6})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a06319aca3da91aa882448df3fe6fcc7aad57a1)
![{\displaystyle \textstyle [1\;8\;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/552624a473ac292cf3241a5fe50234436a414a55)
![{\displaystyle \textstyle [3\;1\;8]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a53695813c4af968c0a83238d0771434f596997d)
![{\displaystyle \textstyle [7\;9\;6\;2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506e5ce4f8483fe46a74d4f40d9a5732caeefa99)

![{\displaystyle {\begin{array}{l}\;[8\;3\;1]^{2}\;=\;(8_{1}\;3_{8}\;1_{3})\,(8_{1}\;3_{8}\;1_{3})=(3_{1}\;1_{8}\;8_{3})\\\;[8\;3\;1]^{3}\;=\;(3_{1}\;1_{8}\;8_{3})\,(8_{1}\;3_{8}\;1_{3})=(1_{1}\;8_{8}\;3_{3})=e\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765020764baef0faea2ace540e43966602f729eb)






















