Равноускоренная система отсчета — различия между версиями
WikiSysop (обсуждение | вклад) (Новая страница: «{| width="100%" | width="40%"|Ускоренное движение << ! width="20%"|Оглавление | width=…») |
WikiSysop (обсуждение | вклад) |
||
| (не показана 21 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
{| width="100%" | {| width="100%" | ||
| − | | width="40%"|[[ | + | | width="40%"|[[Мир элементарных частиц]] << |
! width="20%"|[[Релятивистский мир|Оглавление]] | ! width="20%"|[[Релятивистский мир|Оглавление]] | ||
| − | | width="40%" align="right"| >> [[ | + | | width="40%" align="right"| >> [[Время и расстояние в равноускоренной системе]] |
|} | |} | ||
---- | ---- | ||
| + | Рассмотрим систему <math>\textstyle S'</math>, точка <math>\textstyle x'=0</math> которой движется равноускоренно относительно инерциальной системы <math>\textstyle S</math>. Будем считать, что оси <math>\textstyle x</math> и <math>\textstyle x'</math> параллельны и направлены в одну сторону. Во [[Ускоренное движение|второй главе]] был найден закон движении релятивистски равноускоренной частицы, координата которой изменяется со временем следующим образом: | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> x(t)=\frac{1}{a}\,\bigl[\sqrt{1+(at)^2}-1\bigr]. </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.1)'''</div> | ||
| + | |} | ||
| + | |||
| + | Будем считать, что начало системы <math>\textstyle S'</math> (и наблюдатель находящийся в этой точке) движутся в соответствии с уравнением (4.1) | ||
| + | |||
| + | <center>[[File:nonin_SSp.png]]</center> | ||
| + | |||
| + | Основная особенность неинерциальной системы — это неизотропность пространства внутри неё. Точнее, пространство изотропно в плоскости <math>\textstyle (y',z')</math>, перпендикулярной к ускорению, но неизотропно вдоль оси <math>\textstyle x'</math>. | ||
| + | |||
| + | Пусть ускорение невелико (хотя, возможно, велика скорость системы <math>\textstyle S'</math> относительно <math>\textstyle S</math>). Тогда наблюдатель, находящийся в начале системы <math>\textstyle S'</math>, по крайней мере локально, воспринимает окружающие физические явления подобно "наблюдателю классической механики". В частности, он может пренебречь неизотропностью пространства в отношении эталонов длины. Это означает, что игнорируется возможность их деформации или вводятся соответствующие поправки на упругость материала, из которого сделаны линейки. В результате линейки можно поворачивать, считая что они не изменяются при повороте из изотропной плоскости <math>\textstyle (y',z')</math> в направлении ускорения. Аналогично мы, находясь на поверхности Земли и испытывая ускорение <math>\textstyle g=9.8\;m/s^2</math>, пользуемся "жёсткими" линейками в своей непосредственной окрестности. | ||
| + | |||
| + | Неизотропность приводит к тому, что свободные частицы уже не движутся по прямолинейным траекториям. Эти траектории изгибаются в направлении, противоположном вектору ускорения. Естественно относительно инерциальной системы отсчёта они по-прежнему движутся равномерно и прямолинейно. Так как физика в инерциальной системе нам известна, можно описать и многие из явления, с точки зрения неинерциальных наблюдателей. | ||
| + | |||
| + | Кроме линеек наблюдателю необходимы часы. Чтобы не обсуждать влияние сил инерции на механизм часов, будем считать, что для измерения времени служат некоторые процессы, происходящие в изотропной плоскости <math>\textstyle (y',z')</math>. Например, это может быть шарик, катящийся без трения по круговому желобу, расположенному перпендикулярно движению. Понятно, что существуют разновидности часов, которые откажутся работать в неинерциальной системе, как, впрочем, и наоборот. Например, маятниковые часы с подвесом на оси <math>\textstyle x'</math> под воздействием ''постоянных'' сил инерции будут ''равномерно'' "тикать", а при переходе в инерциальную систему — сломаются, так как возникнет "невесомость". | ||
| + | |||
| + | Тем не менее, предположим, что в равноускоренной системе отсчёта существует достаточно широкий класс синхронно идущих часов в данной точке пространства. Синхронность подразумевает, что законы движения частиц получаются одинаковыми при использовании различных часов. При этом, как и раньше, для измерения времени выбираются процессы, относительно которых все остальные движения выглядят [[Неподвижные наблюдатели|наиболее просто (см. Глава 1.)]]. Например, координата <math>\textstyle y'</math> свободно движущейся частицы, в силу изотропности пространства в плоскости <math>\textstyle (y',z')</math>, за равные промежутки времени должна изменяться на равные величины. Далее нам потребуется важное ''допущение'' о том, что <blockquote> темп времени движущихся часов относительно неподвижных часов зависит только от их скорости и ''не зависит от ускорения''. </blockquote> Если в момент времени <math>\textstyle t'=t=0</math> начала систем совпадали и скорость <math>\textstyle S'</math> относительно <math>\textstyle S</math> была нулевой, то спустя некоторое время, связь показаний движущихся часов <math>\textstyle t'</math> (находящихся в начале координат) и синхронизированых неподвижных, расставленых вдоль траектории движения [[Ускоренное движение|будет иметь вид]]: | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> t'=\frac{1}{a}\,\mathrm{ash}\,(at)\;\;\;\;\;\;\;\;\;или\;\;\;\;\;\;\;\;\;\;\;\;at=\mathrm{ch}(at'). </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.2)'''</div> | ||
| + | |} | ||
| + | |||
| + | Каким бы ни было значение <math>\textstyle a</math>, всегда можно выбрать малый интервал времени, при котором скорость ускоряющихся часов меняется незначительно, и их можно рассматривать как локально инерциальную систему отсчета. Это общее соображение имеет и экспериментальные подтверждения. Так, время жизни мюонов в кольцевом ускорителе | ||
| + | <ref>Bailey J. et al. — "''Measurements of relativistic time dilatation for positive and negative muons in circular orbit''", Nature, v.268, p.301-305 (1977) | ||
| + | </ref> в пределах относительной ошибки <math>\textstyle 2\cdot 10^{-3}</math> увеличивается в соответствии с релятивистской формулой. При этом скорость мюонов составляет <math>\textstyle v=0.9994</math> и время замедляется в <math>\textstyle 1/\sqrt{1-v^2}=29</math> раз. При 7 метровом радиусе кольца, ускорение достигает значений <math>\textstyle a\sim 10^{18}\cdot g</math>, где <math>\textstyle g=9.8\,m/s^2</math>. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | <math>\textstyle \bullet</math> Представим теперь эскадру из двух космических кораблей, разделённых расстоянием <math>\textstyle x_0</math>, которая начинает ускоренное движение относительно инерциальной системы отсчёта <math>\textstyle S</math>. Пока корабли стояли в космопортах, их экипажи синхронизовали свои часы друг с другом и остальными наблюдателями в системе <math>\textstyle S</math>. Время на часах первого корабля, стартовавшего из <math>\textstyle x=0</math>, обозначим через <math>\textstyle t'</math>, а второго, стартовавшего из <math>\textstyle x=x_0</math>, через <math>\textstyle t''</math>. В инерциальной системе отсчёта время единое и равно <math>\textstyle t</math>. При <math>\textstyle t=t'=t''=0</math> корабли начинают равноускоренное движение, постоянно увеличивая свою скорость. | ||
| + | |||
| + | <center>[[File:nonin_2space.png]]</center> | ||
| + | |||
| + | Координата первого (левого) корабля, находящегося в начале системы <math>\textstyle S'</math> изменяется со временем в соответствии с (4.1) | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> x(t)=\frac{1}{a}\,\bigl[\sqrt{1+(at)^2}-1\bigr]=\frac{1}{a}\,\bigl[\mathrm{ch}(at')-1\bigr], </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.3)'''</div> | ||
| + | |} | ||
| + | |||
| + | где во втором равенстве подставлено собственное время корабля (4.2). | ||
| + | |||
| + | ''Жёсткая система отсчёта'' — это множество неподвижных относительно друг друга наблюдателей. Мы задали траекторию <math>\textstyle x(t)</math> начала системы отсчёта <math>\textstyle S'</math>. Как должен двигаться второй космический корабль, чтобы расстояние между кораблями эскадры оставалось неизменным с ''их точки зрения''? Ответ "так же" не является верным. События, одновременные в одной системе отсчёта, будут неодновременными в другой. Если корабли синхронно ускоряются с точки зрения системы <math>\textstyle S</math>, то это ускорение не будет синхронным в <math>\textstyle S'</math>, и наоборот. Это приводит к тому, что неизменность расстояния между точками неинерциальной системы отсчёта <math>\textstyle S'</math> — ''понятие относительное''. Если наблюдатели в <math>\textstyle S'</math> "выдерживают" свою систему жёсткой, то наблюдатели в инерциальной системе <math>\textstyle S</math> будут регистрировать, её сжатие в направлении движения. События (ускорительные импульсы корабля) по ходу движения в системе <math>\textstyle S'</math> происходят позже по сравнению с событиями расположенными против хода (см. [[Время]]), и второй корабль в системе <math>\textstyle S</math> разгоняется медленнее. | ||
| + | |||
| + | Как эскадра кораблей должна выдерживать неизменным расстояние? Будем считать, что для этого используется "радиолокационный метод". Один корабль посылает световой сигнал в сторону второго корабля. Этот сигнал отражаясь, возвращается обратно. Время движения туда-обратно по ''локальным часам'' корабля не должно изменяться. Выясним, по какой траектории <math>\textstyle f(t)</math> должен двигаться второй корабль ''относительно системы'' <math>\textstyle S</math>, чтобы система отсчёта <math>\textstyle S'</math> ''для её экипажей'' была жесткой. | ||
| + | |||
| + | Расчёты проведём в неподвижной системе <math>\textstyle S</math>. Пусть первый корабль в момент времени <math>\textstyle t_1</math> отправляет вперёд световой сигнал, который достигает второго корабля в момент времени <math>\textstyle t</math>, отражается и возвращается обратно в момент времени <math>\textstyle t_2</math>: | ||
| + | |||
| + | <center>[[File:noninerframe1.png]]</center> | ||
| + | |||
| + | Все времена измеряются по часам инерциальной системы отсчёта <math>\textstyle S</math>. Координата первого корабля равна <math>\textstyle x(t)</math>, см. (4.3), второго — <math>\textstyle f(t)</math>. Запишем время ухода <math>\textstyle t_1=\mathrm{ch}(at'_1)/a</math> и возвращения <math>\textstyle t_2=\mathrm{ch}(at'_2)/a</math> сигнала ''по часам первого корабля'' (<math>\textstyle t'_1</math> и <math>\textstyle t'_2</math>): | ||
| + | |||
| + | :<center><math>\left\{ \begin{array}{l} \displaystyle f(t)-t =x(t_1) - t_1= \frac{1}{a}\,\bigl[\mathrm{ch}(at'_1)-1\bigr]-\frac{1}{a}\,\mathrm{ch}(at'_1)=\frac{1}{a}\,\left(e^{-at'_1}-1\right)\\[4mm] \displaystyle f(t)+t =x(t_2) + t_2= \frac{1}{a}\,\bigl[\mathrm{ch}(at'_2)-1\bigr]+\frac{1}{a}\,\mathrm{ch}(at'_2)=\frac{1}{a}\,\left(e^{+at'_2}-1\right). \end{array} \right.</math></center> | ||
| + | |||
| + | Если расстояние между кораблями неизменно, то время движения сигнала "туда и обратно" <math>\textstyle \tau_0=t'_2-t'_1=const</math> не зависит от момента его посылки <math>\textstyle t'_1</math>. Вычитая уравнения системы, находим: | ||
| + | |||
| + | :<center><math>2at=e^{at'_2}-e^{-a\,(t'_2-\tau_0)}\;\;\;\;\;\;\;\;=>\;\;\;\;\;\;\;e^{at'_2}=at+\sqrt{e^{a\tau_0}+(at)^2}.</math></center> | ||
| + | |||
| + | В качестве решения квадратного уравнения относительно <math>\textstyle e^{at'_2}</math> выбран положительный корень, подставляя который во второе уравнение системы, получаем искомую траекторию <math>\textstyle f(t)</math>: | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> a\,f(t)=\sqrt{e^{a\tau_0}+(at)^2}-1=\sqrt{(1+ax_0)^2+(at)^2}-1, </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.4)'''</div> | ||
| + | |} | ||
| + | |||
| + | где в последнем равенстве учтено начальное условие <math>\textstyle f(0)=x_0</math>. Назовём ''радиолокационным расстоянием'' половину времени <math>\textstyle \tau_0</math> от движения сигнала в обе стороны: | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> x'_0 = \frac{t'_2-t'_1}{2} =\frac{\tau_0}{2} = \frac{1}{a}\ln(1+ax_0). </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.5)'''</div> | ||
| + | |} | ||
| + | |||
| + | Скорость второго корабля относительно неподвижной системы отсчёта <math>\textstyle S</math> равна <math>\textstyle u_2(t)=df(t)/dt</math>, поэтому: | ||
| + | |||
| + | {| width="100%" | ||
| + | | width="90%" align="center"|<math> u_2(t) = \frac{at}{\sqrt{(1+ax_0)^2+(at)^2}},\;\;\;или\;\;\;\frac{u_2(t)}{\sqrt{1-u^2_2(t)}} = \frac{at}{1+ax_0}. </math> | ||
| + | | <div width="10%" align="right" style="color:#0000CC">'''(4.6)'''</div> | ||
| + | |} | ||
| + | |||
| + | Сравнивая это выражение с формулой [[Ускоренное движение|равноускоренного движения]] (2.19), приходим к выводу, что второй корабль также движется равноускоренно, но с собственным ускорением <math>\textstyle a_2=a/(1+a x_0)</math>. | ||
| + | |||
| + | == Литература == | ||
| + | |||
| + | <references /> | ||
---- | ---- | ||
{| width="100%" | {| width="100%" | ||
| − | | width="40%"|[[ | + | | width="40%"|[[Мир элементарных частиц]] << |
! width="20%"|[[Релятивистский мир|Оглавление]] | ! width="20%"|[[Релятивистский мир|Оглавление]] | ||
| − | | width="40%" align="right"| >> [[ | + | | width="40%" align="right"| >> [[Время и расстояние в равноускоренной системе]] |
|} | |} | ||
---- | ---- | ||
[[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | [[Релятивистский мир]] - лекции по теории относительности, гравитации и космологии | ||
Текущая версия на 09:36, 12 апреля 2011
| Мир элементарных частиц << | Оглавление | >> Время и расстояние в равноускоренной системе |
|---|
Рассмотрим систему , точка которой движется равноускоренно относительно инерциальной системы . Будем считать, что оси и параллельны и направлены в одну сторону. Во второй главе был найден закон движении релятивистски равноускоренной частицы, координата которой изменяется со временем следующим образом:
(4.1)
|
Будем считать, что начало системы (и наблюдатель находящийся в этой точке) движутся в соответствии с уравнением (4.1)
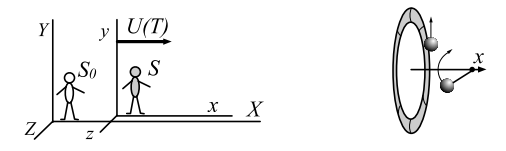
Основная особенность неинерциальной системы — это неизотропность пространства внутри неё. Точнее, пространство изотропно в плоскости , перпендикулярной к ускорению, но неизотропно вдоль оси .
Пусть ускорение невелико (хотя, возможно, велика скорость системы относительно ). Тогда наблюдатель, находящийся в начале системы , по крайней мере локально, воспринимает окружающие физические явления подобно "наблюдателю классической механики". В частности, он может пренебречь неизотропностью пространства в отношении эталонов длины. Это означает, что игнорируется возможность их деформации или вводятся соответствующие поправки на упругость материала, из которого сделаны линейки. В результате линейки можно поворачивать, считая что они не изменяются при повороте из изотропной плоскости в направлении ускорения. Аналогично мы, находясь на поверхности Земли и испытывая ускорение , пользуемся "жёсткими" линейками в своей непосредственной окрестности.
Неизотропность приводит к тому, что свободные частицы уже не движутся по прямолинейным траекториям. Эти траектории изгибаются в направлении, противоположном вектору ускорения. Естественно относительно инерциальной системы отсчёта они по-прежнему движутся равномерно и прямолинейно. Так как физика в инерциальной системе нам известна, можно описать и многие из явления, с точки зрения неинерциальных наблюдателей.
Кроме линеек наблюдателю необходимы часы. Чтобы не обсуждать влияние сил инерции на механизм часов, будем считать, что для измерения времени служат некоторые процессы, происходящие в изотропной плоскости . Например, это может быть шарик, катящийся без трения по круговому желобу, расположенному перпендикулярно движению. Понятно, что существуют разновидности часов, которые откажутся работать в неинерциальной системе, как, впрочем, и наоборот. Например, маятниковые часы с подвесом на оси под воздействием постоянных сил инерции будут равномерно "тикать", а при переходе в инерциальную систему — сломаются, так как возникнет "невесомость".
Тем не менее, предположим, что в равноускоренной системе отсчёта существует достаточно широкий класс синхронно идущих часов в данной точке пространства. Синхронность подразумевает, что законы движения частиц получаются одинаковыми при использовании различных часов. При этом, как и раньше, для измерения времени выбираются процессы, относительно которых все остальные движения выглядят наиболее просто (см. Глава 1.). Например, координата свободно движущейся частицы, в силу изотропности пространства в плоскости , за равные промежутки времени должна изменяться на равные величины. Далее нам потребуется важное допущение о том, что
темп времени движущихся часов относительно неподвижных часов зависит только от их скорости и не зависит от ускорения.
Если в момент времени начала систем совпадали и скорость относительно была нулевой, то спустя некоторое время, связь показаний движущихся часов (находящихся в начале координат) и синхронизированых неподвижных, расставленых вдоль траектории движения будет иметь вид:
| Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle t'=\frac{1}{a}\,\mathrm{ash}\,(at)\;\;\;\;\;\;\;\;\;или\;\;\;\;\;\;\;\;\;\;\;\;at=\mathrm{ch}(at'). } | (4.2)
|
Каким бы ни было значение , всегда можно выбрать малый интервал времени, при котором скорость ускоряющихся часов меняется незначительно, и их можно рассматривать как локально инерциальную систему отсчета. Это общее соображение имеет и экспериментальные подтверждения. Так, время жизни мюонов в кольцевом ускорителе [1] в пределах относительной ошибки увеличивается в соответствии с релятивистской формулой. При этом скорость мюонов составляет и время замедляется в раз. При 7 метровом радиусе кольца, ускорение достигает значений , где .
Представим теперь эскадру из двух космических кораблей, разделённых расстоянием , которая начинает ускоренное движение относительно инерциальной системы отсчёта . Пока корабли стояли в космопортах, их экипажи синхронизовали свои часы друг с другом и остальными наблюдателями в системе . Время на часах первого корабля, стартовавшего из , обозначим через , а второго, стартовавшего из , через . В инерциальной системе отсчёта время единое и равно . При корабли начинают равноускоренное движение, постоянно увеличивая свою скорость.

Координата первого (левого) корабля, находящегося в начале системы изменяется со временем в соответствии с (4.1)
(4.3)
|
где во втором равенстве подставлено собственное время корабля (4.2).
Жёсткая система отсчёта — это множество неподвижных относительно друг друга наблюдателей. Мы задали траекторию начала системы отсчёта . Как должен двигаться второй космический корабль, чтобы расстояние между кораблями эскадры оставалось неизменным с их точки зрения? Ответ "так же" не является верным. События, одновременные в одной системе отсчёта, будут неодновременными в другой. Если корабли синхронно ускоряются с точки зрения системы , то это ускорение не будет синхронным в , и наоборот. Это приводит к тому, что неизменность расстояния между точками неинерциальной системы отсчёта — понятие относительное. Если наблюдатели в "выдерживают" свою систему жёсткой, то наблюдатели в инерциальной системе будут регистрировать, её сжатие в направлении движения. События (ускорительные импульсы корабля) по ходу движения в системе происходят позже по сравнению с событиями расположенными против хода (см. Время), и второй корабль в системе разгоняется медленнее.
Как эскадра кораблей должна выдерживать неизменным расстояние? Будем считать, что для этого используется "радиолокационный метод". Один корабль посылает световой сигнал в сторону второго корабля. Этот сигнал отражаясь, возвращается обратно. Время движения туда-обратно по локальным часам корабля не должно изменяться. Выясним, по какой траектории должен двигаться второй корабль относительно системы , чтобы система отсчёта для её экипажей была жесткой.
Расчёты проведём в неподвижной системе . Пусть первый корабль в момент времени отправляет вперёд световой сигнал, который достигает второго корабля в момент времени , отражается и возвращается обратно в момент времени :

Все времена измеряются по часам инерциальной системы отсчёта . Координата первого корабля равна , см. (4.3), второго — . Запишем время ухода и возвращения сигнала по часам первого корабля ( и ):
Если расстояние между кораблями неизменно, то время движения сигнала "туда и обратно" не зависит от момента его посылки . Вычитая уравнения системы, находим:
В качестве решения квадратного уравнения относительно выбран положительный корень, подставляя который во второе уравнение системы, получаем искомую траекторию :
(4.4)
|
где в последнем равенстве учтено начальное условие . Назовём радиолокационным расстоянием половину времени от движения сигнала в обе стороны:
(4.5)
|
Скорость второго корабля относительно неподвижной системы отсчёта равна , поэтому:
| Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle u_2(t) = \frac{at}{\sqrt{(1+ax_0)^2+(at)^2}},\;\;\;или\;\;\;\frac{u_2(t)}{\sqrt{1-u^2_2(t)}} = \frac{at}{1+ax_0}. } | (4.6)
|
Сравнивая это выражение с формулой равноускоренного движения (2.19), приходим к выводу, что второй корабль также движется равноускоренно, но с собственным ускорением .
Литература
- Перейти ↑ Bailey J. et al. — "Measurements of relativistic time dilatation for positive and negative muons in circular orbit", Nature, v.268, p.301-305 (1977)
| Мир элементарных частиц << | Оглавление | >> Время и расстояние в равноускоренной системе |
|---|
Релятивистский мир - лекции по теории относительности, гравитации и космологии





![{\displaystyle x(t)={\frac {1}{a}}\,{\bigl [}{\sqrt {1+(at)^{2}}}-1{\bigr ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a582d5b248748d6532a12218ef59b7e5a11b6ab)


















![{\displaystyle x(t)={\frac {1}{a}}\,{\bigl [}{\sqrt {1+(at)^{2}}}-1{\bigr ]}={\frac {1}{a}}\,{\bigl [}\mathrm {ch} (at')-1{\bigr ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/389ccfe243766cecb8db4dc3ed5fa7bfa4bc064b)








![{\displaystyle \left\{{\begin{array}{l}\displaystyle f(t)-t=x(t_{1})-t_{1}={\frac {1}{a}}\,{\bigl [}\mathrm {ch} (at'_{1})-1{\bigr ]}-{\frac {1}{a}}\,\mathrm {ch} (at'_{1})={\frac {1}{a}}\,\left(e^{-at'_{1}}-1\right)\\[4mm]\displaystyle f(t)+t=x(t_{2})+t_{2}={\frac {1}{a}}\,{\bigl [}\mathrm {ch} (at'_{2})-1{\bigr ]}+{\frac {1}{a}}\,\mathrm {ch} (at'_{2})={\frac {1}{a}}\,\left(e^{+at'_{2}}-1\right).\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48729b9ca69c78d2fdaaf86b14b29fee9fc2c9c)








