Время и расстояние в равноускоренной системе

Равноускоренная система отсчета <<	Оглавление	>> Неинерциальные координаты и время

---

Разберёмся, почему ускорение второго корабля оказалось меньше. Траектории обоих кораблей известны, поэтому можно записать показания часов каждого из них в момент времени $\textstyle t$:

$t={\frac {1}{a}}\mathrm {ch} (at'),\;\;\;\;\;\;\;\;\;\;t={\frac {1+ax_{0}}{a}}\,\mathrm {ch} \left({\frac {at''}{1+ax_{0}}}\right).$

Заметим, что время $\textstyle t'$, прошедшее на первом корабле, и $\textstyle t''$ на втором сравнивается с различными часами, синхронизированными в системе $\textstyle S$. Запишем координту второго корабля через его собственное время:

$f(t)={\frac {1}{a}}\,{\bigl [}{\sqrt {(1+ax_{0})^{2}+(at)^{2}}}-1{\bigr ]}={\frac {1+ax_{0}}{a}}\mathrm {ch} \left({\frac {at''}{1+ax_{0}}}\right)-{\frac {1}{a}}.$

Пусть второй (правый) корабль посылает "сигнал точного времени" в направлении первого корабля. Он уходит в момент времени $\textstyle t''_{1}$ и приходит к первому кораблю в момент $\textstyle t'_{2}$, проходя с единичной скоростью ($\textstyle c=1$) в системе $\textstyle S$ расстояние $\textstyle f(t_{1})-x(t_{2})=t_{2}-t_{1}$, или $\textstyle f(t_{1})+t_{1}=x(t_{2})+t_{2}$. Запишем это уравнение во временах каждого корабля:

$(1+ax_{0})\,\left[\mathrm {ch} \left({\frac {a\,t''_{1}}{1+ax_{0}}}\right)+\mathrm {ch} \left({\frac {a\,t''_{1}}{1+ax_{0}}}\right)\right]=\mathrm {ch} (a\,t'_{2})+\mathrm {ch} (a\,t'_{2}).$

Выражая гиперболические функции через экспоненты, получаем линейную связь времён и "радиолокационного расстояния" $\textstyle x'_{0}=\ln(1+ax_{0})/a$:

$t'_{2}=x'_{0}+t''_{1}\,e^{-ax'_{0}}.$

(4.7)

Сигналы, отправленные через равные промежутки времени, по часам второго корабля будут также приходить через равные промежутки, однако с другим интервалом:

Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \Delta t' = \Delta t''\,e^{-ax'_0},\;\;\;\;\;\;\;или\;\;\;\;\;\;\;\nu'=\nu''\,e^{ax'_0}.}

Частота принятого сигнала $\textstyle \nu '$ от удалённого наблюдателя равноускоренной системы тем больше, чем дальше по ходу движения находится источник сигнала.

Таким образом, если расстояние между наблюдателями в неинерциальной системе отсчета остаётся неизменным, то время у них течёт различным образом. Чем дальше по направлению ускорения находятся часы, тем быстрее на них идёт время.

---

$\textstyle \bullet$ Наблюдатели в ускоренной системе отсчёта чувствуют себя точно так же, как и мы на Земле, находясь в однородном поле силы тяжести. В частности, все объекты, "выпущенные из рук", независимо от их массы приобретают ускорение $\textstyle a$.

Если, следуя Эйнштейну, считать, что равноускоренная система неотличима от однородного гравитационного поля, то полученная формула для частот должна выполняться и в земных условиях. В частности, приёмник, расположенный ниже источника эталонного излучения $\textstyle \nu _{0}$, должен получать сигнал с большей частотой $\textstyle \nu \approx \nu _{0}\,(1+gH/c^{2})$, где Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle g=9.8\;м/c^2} , а $\textstyle H$ — высота источника над приёмником, и восстановлена константа "$\textstyle c$". Это соотношение с хорошей точностью подтвердилось в эксперименте Паунда и Ребки (1960 г.). Их установка имела высоту Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \textstyle H=22.5\,м} , что соответствовало относительному изменению частоты $\textstyle gH/c^{2}=2.5\cdot 10^{-15}$, которое удалось измерить при помощи эффекта Мёссбауэра.

Слагаемое $\textstyle x'_{0}=\ln(1+ax_{0})/a$ в формуле (4.7) — это время распространения света при передаче сигнала по часам первого корабля. Действительно, в (4.4) мы определили $\textstyle e^{a\tau _{0}/2}=1+ax_{0}$. Время движения "туда и обратно" светового импульса $\textstyle \tau _{0}=t'_{2}-t'_{1}$ может быть принято первым кораблём за удвоенное расстояние $\textstyle x'$ до второго корабля. С учётом времени на прохождение этого расстояния, наблюдатели могут сравнить показания своих часов $\textstyle t'$ и $\textstyle t$:

$t'=t''\,e^{-ax'_{0}}.$

(4.8)

В результате событие, произошедшее на втором корабле в момент $\textstyle t''$, наблюдатель на первом может считать одновременным моменту его часов $\textstyle t'=t''/(1+ax_{0})$, так как информация о нём достигнет первого корабля через время, равное расстоянию $\textstyle x'$.

Напомним, что расстояние между кораблями до старта равнялось $\textstyle x_{0}$. Как только появилось ускорение, пространство стало неизотропным и расстояние до второго корабля $\textstyle x_{0}\mapsto x'$ уменьшилось, и в дальнейшем уже не менялось. На самом деле, скачок расстояния наблюдатели обнаружат после старта, спустя некоторое время, необходимое для проведения его радиолокационного измерения. В момент отключения двигателей неинерциальная система отсчёта превращается в инерциальную, и пространство снова становится изотропным. Расстояние между кораблями увеличится с величины $\textstyle x'_{0}=\ln(1+ax_{0})/a$ до значения $\textstyle x_{0}$.

Радиолокационный метод, проведенный наблюдателем на первом корабле привёл к расстоянию между кораблями равному $\textstyle x'_{0}=\ln(1+ax_{0})/a$. Посмотрим, что получится, если такое же измерение проведёт наблюдатель на втором корабле. Запишем процесс посылки и получения сигнала обратно с точки зрения системы $\textstyle S$:

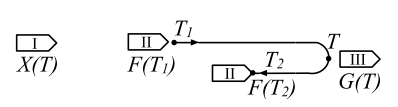
Из этих двух уравнений следует:

${\bigl (}1+af(t_{1})+at_{1}{\bigr )}{\bigl (}1+af(t_{2})-at_{2}{\bigr )}={\bigl (}1+ax(t)+at{\bigr )}{\bigl (}1+ax(t)-at{\bigr )}=1,$

где во втором равенстве учтён явный вид функции $\textstyle x(t)$ (4.1). Переходя ко времени второго корабля $\textstyle at=(1+ax_{0})\mathrm {ch} (at''/(1+ax_{0}))$, имеем:

$\left[\mathrm {ch} {\frac {at''_{1}}{1+ax_{0}}}+\mathrm {ch} {\frac {at''_{1}}{1+ax_{0}}}\right]\left[\mathrm {ch} {\frac {at''_{2}}{1+ax_{0}}}-\mathrm {ch} {\frac {at''_{2}}{1+ax_{0}}}\right]={\frac {1}{(1+ax_{0})^{2}}}=e^{-2ax'_{0}}.$

Записав гиперболические функции через экспоненты, из этого уравнения несложно получить значение длительности прохождения сигнала в обе стороны:

$x''_{0}={\frac {t''_{2}-t''_{1}}{2}}=x'_{0}\,e^{ax'_{0}}.$

(4.9)

Таким образом, второй наблюдатель получит в $\textstyle e^{ax'_{0}}$ большее расстояние, чем первый. Если повторить расчёт по посылке периодических сигналов (стр.\pageref{acsel_ref_sys_times}), но теперь от первого корабля ко второму, то получится соотношение:

$t''_{2}=x''_{0}+t'_{1}\,e^{ax'_{0}}.$

(4.10)

В результате второй корабль от первого будет получать сигналы с меньшей частотой

$\nu ''=\nu '\,e^{-ax'_{0}}.$

Таким образом, мы не только не можем говорить о едином времени в неинерциальной системе, но и координаты (расстояния от начала отсчёта) являются величинами, измеряемыми конкретными наблюдателями. Например, $\textstyle x'_{0}$ в (4.8) получается в результате радиолокационных измерений наблюдателя на первом корабле, а $\textstyle x''_{0}$ в (4.9) для наблюдателя на втором. Они не совпадают. Это и понятно. В радиолокационном методе используются часы. Если время для различных наблюдателей в неинерциальной системе течёт по-разному, то и результаты радиолокации будут различными.

---

$\textstyle \bullet$ В процессе движения, расстояние между кораблями в неинерциальной системе отчёта выдерживается неизменным при помощи радиолокационного метода. Для неподвижных наблюдателей в системе $\textstyle S$, расстояние между кораблями уменьшается. С точки зрения стандартного сокращения Лоренца в этом нет ни чего удивительного, так как скорость кораблей всё время растёт.

Представим "линейку", соединяющую оба корабля. Её длина в системе $\textstyle S$ равна:

$l(t)=f(t)-x(t)={\frac {1}{a}}{\sqrt {(1+a\,x_{0})^{2}+(at)^{2}}}-{\frac {1}{a}}{\sqrt {(1+(at)^{2}}},$

Наблюдатель системы $\textstyle S'$, находящийся на первом корабле, считает, что длина линейки (расстояние между кораблями) равна

$l_{0}=x'_{0}={\frac {1}{a}}\ln(1+ax_{0}).$

(4.11)

Если ввести скорость первого корабля относительно неподвижной инерциальной системы отсчёта и соответствующий этой скорости фактор Лоренца:

$u(t)={\frac {dx}{dt}}={\frac {at}{\sqrt {1+(at)^{2}}}},\;\;\;\;\;\;\;\gamma ={\frac {1}{\sqrt {1-u^{2}(t)}}}={\sqrt {1+(at)^{2}}},$

то выражение для длины можно переписать следующим образом:

$l(t)={\frac {{\sqrt {e^{2al_{0}}+\gamma ^{2}-1}}-\gamma }{a}}\approx {\frac {l_{0}}{\gamma }},$

где приближённое равенство записано в первом приближении по собственному ускорению $\textstyle a$. Для этого, экспонента раскладывается в ряд $\textstyle e^{x}\approx 1+x$, и для корня используется разложение $\textstyle {\sqrt {1+x}}\approx 1+x/2$.

Таким образом, если собственное ускорение мало, то зависимость длины стержня совпадает с лоренцевским сокращением $\textstyle l=l_{0}{\sqrt {1-u^{2}}}$ для двух инерциальных систем отсчёта. В общем же случае, сокращение линейки отличается от лоренцевского.

Подчеркнём, что значение $\textstyle l_{0}$ неинерциальные наблюдатели получают в результате радиолокационного измерения, а не реальным прикладыванием линейки, при помощи которой они измеряют скорости в своей непосредственной окрестности. В соответствии с (4.11) оно отличается от начального расстояния между кораблями $\textstyle x_{0}$ и различно для наблюдателя не первом и втором кораблях. Выше, в качестве собственной длины линейки, было выбрано радиолокационное расстояние, измеренное наблюдателем на первом корабле.

---

$\textstyle \bullet$ Приведём численный пример. Будем считать, что $\textstyle a=1$, время измеряется в годах, а расстояние — в световых годах ($\textstyle c=1$). Пусть оба корабля эскадры, разогнавшись до скорости $\textstyle u$ относительно системы $\textstyle S$, отключают двигатели и начинают двигаться равномерно. Так как темп хода часов на каждом корабле различный, различным будет и время набора требуемой скорости. Пусть первый корабль по часам системы $\textstyle S$ разгоняется в течение одного года $\textstyle t_{1}=1$, достигая скорости $\textstyle u=t/{\sqrt {1+t_{1}^{2}}}=0.71.$ По собственным часам корабля время ускоренного движения составляет $\textstyle t'_{1}=\mathrm {ash} \,t_{1})=0.88$ года. Второй корабль, находящийся при старте на расстоянии одного светового года $\textstyle x_{0}=1$, достигнет этой же скорости (по часам системы $\textstyle S$) в $\textstyle 1+x_{0}$ раза позже [см. (4.6)]:

$t_{2}=(1+x_{0})\,{\frac {u}{\sqrt {1-u^{2}}}}=(1+x_{0})\,t_{1}=2,$

что соответствует его собственному времени $\textstyle t''_{2}$, равному:

$t''_{2}=(1+x_{0})\,\mathrm {ash} \,\left(t_{2}/(1+x_{0})\right)=(1+x_{0})\,t'_{1}=1.76.$

Таким образом, по собственным часам второго корабля на разгон уходит в два раза больше времени, чем на первом.

Для экипажа первого корабля часы на втором корабле идут быстрее в $\textstyle 1+x_{0}$ раз (4.8). Поэтому в $\textstyle S'$ корабли достигнут одинаковой скорости одновременно (в указанном ранее смысле). В то же время, для наблюдателей в $\textstyle S$ события отключения двигателей неодновременные и отстоят друг от друга во времени на один год. В течение разгона часы второго корабля уходят вперёд по сравнению с часами первого корабля. После отключения двигателей система $\textstyle S'$ превращается в инерциальную, и темп хода всех часов становится одинаковым. Однако экипаж флагманского корабля оказывается старше в $\textstyle 1+x_{0}$ раз. В результате корабли вынуждены по-новому синхронизировать свои часы.

Расстояние между кораблями для наблюдателей в $\textstyle S$ после отключения двигателей второго корабля в момент времени $\textstyle t_{2}$ перестаёт изменяться и становится равным:

$f(t_{2})-[x(t_{1})+u\,(t_{2}-t_{1})]=x_{0}{\sqrt {1-u^{2}}}.$

Второе слагаемое в квадратных скобках — это расстояние, которое пролетел первый корабль с постоянной скоростью $\textstyle u$ после отключения двигателя. Таким образом, дистанция между кораблями ($\textstyle x_{0}{\sqrt {1-u^{2}}}$) уменьшилась по сравнению с той, которая была ($\textstyle x_{0}$), когда они стояли на космодромах. Это итоговое сокращение, при любом парамере $\textstyle a$, в точности соответствует лоренцевскому сжатию линейки.

---

Подведём некоторые итоги. Мы выбрали устройство часов в неинерциальной системе отсчёта (НИСО) таким образом, чтобы скорость свободных частиц в плоскости, перпендикулярной ускорению была постоянной. Затем предположили, что ход таких часов с точки зрения наблюдателей в "неподвижной" инерциальной системе отсчёта (ИСО) замедляется так же, как и в сопутствующей ИСО, которая движется с той же скоростью, что и НИСО. Собственно неинерциальной системой отсчёта мы назвали совокупность наблюдателей, расстояние между которыми, измеряемое при помощи световых сигналов (радиолокации), неизменно по их часам. Однако для наблюдателей в ИСО такая НИСО уже не выглядит жёсткой и все её точки вдоль направления движения имеют различные скорости.

Обмен наблюдателями световыми сигналами приводит к выводу, что время в различных точках НИСО течёт различным образом. Аналогично, расстояние между двумя наблюдателями в НИСО хотя и постоянно, но имеет различное значение для каждого из них.

Мы не использовали свойств скорости световых сигналов в НИСО. Однако, расстояние, полученное а результате радиолокационного измерения, считалось неизменным. Поэтому фактически предполагалось постоянство скорости света в НИСО (но не обязательно её изотропность) вдоль оси $\textstyle x$. В дальнейшем мы примем более сильное допущение:

Скорость светового сигнала в неинерциальной системе отсчёта остаётся постоянной вдоль траектории его движения.

Разберёмся с физическими предпосылками этого допущения. В любой момент времени можно представить, что рядом с некоторым наблюдателем в НИСО с той же скоростью движется инерциальный наблюдатель. Для него фундаментальная скорость (скорость света) постоянна во всех направлениях и является максимально возможной скоростью движения любого объекта. Находясь рядом, инерциальный и неинерциальный наблюдатели имеют одинаковую скорость и темп хода времени. Они без труда могут согласовать свои единицы измерения. Спустя некоторое время скорость неинерциального наблюдателя изменится и рядом с ним может оказаться другой инерциальный наблюдатель. Если у первого и второго инерциальных наблюдателей единицы измерений были согласованы, то они окажутся согласованными между неинерциальным наблюдателем и вторым инерциальным. Это утверждение основано на определении темпа замедления времени в НИСО, неизменности линеек в перпендикулярном к ускорению напралению. Поэтому измерения скорости света в эти два последовательные момента времени окажутся одинаковыми по величине и направлению.

---

Равноускоренная система отсчета <<	Оглавление	>> Неинерциальные координаты и время

---

Релятивистский мир - лекции по теории относительности, гравитации и космологии